Secondaire 5 • 2a
BOnjour,
Je ne comprends pas comment dans le corrigé c'est ca la reponse, mon prof me dit de decortiquer en faisant des graphiques j'aie fais et je ne nobyiens pas la bonne reponse qui est en noir
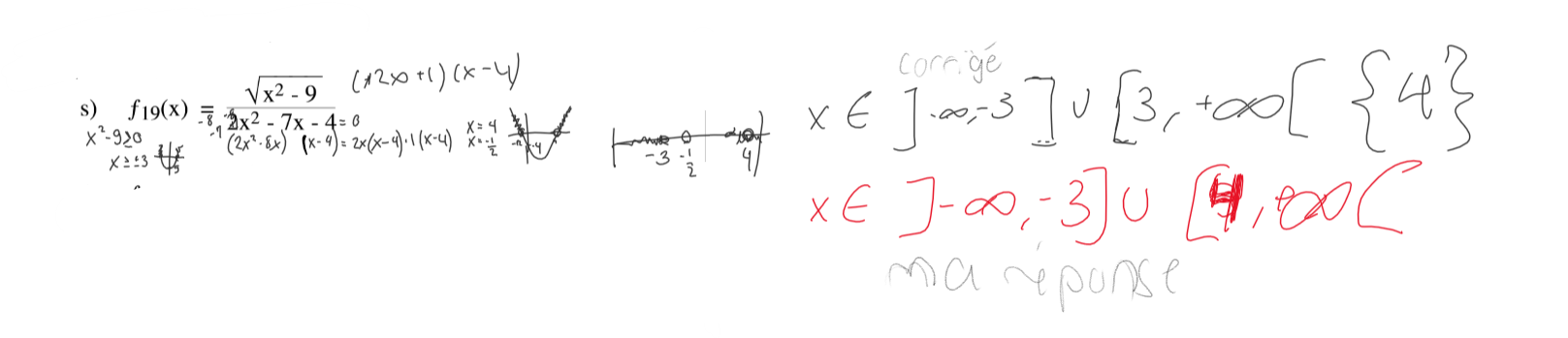






bonjour,
Je comprends qu'on cherche le domaine ...
\(\)
Il faut \(x^2-9\geq 0\) → \(x\leq -3\) ou \(x\geq3\)
Il ne faut pas que \(2x^2-7x-4=0\) → \(x\neq\tfrac{-1}{2}\) et \(x\neq4\).
Réponse:
]-infini, -3] U [3, +infini[ \ {4}
on pourrait aussi écrire
]-infini, -3] U [3, 4[ U ]4, +infini[
Bonjour, en effet les explications de FerUpsilon sont exactes
Quand tu bloques sur ce genre de numéro, je t'invite à t'aider des ressources disponibles !
Entre autre Desmos , qui est un représentation de graphique !
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
En écrivant l'équation, tu as un aperçu du graphique.
Bien sur, ne l'utilise pas toujours, car tu n'en auras pas accès aux examens, mais lorsque tu bloques, cela peut être une bonne ressource !
N'Hésite pas si tu as d'autres questions
VC
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Quand la valeur de x se trouve dans l'intervalle ]-3,3[ la racine carrée de x^2 - 9 = (x-3)(x+3) est alors la racine carrée d'un nombre négatif.
Je ne pense pas qu'on voit les nombres complexes en secondaire 5.
Par ailleurs il y a une asymptote en x=4 si tu décomposes 2x^2 - 7x - 4 tu devrais le réaliser.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!