Zone d’entraide

ZombieOmicron9053

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

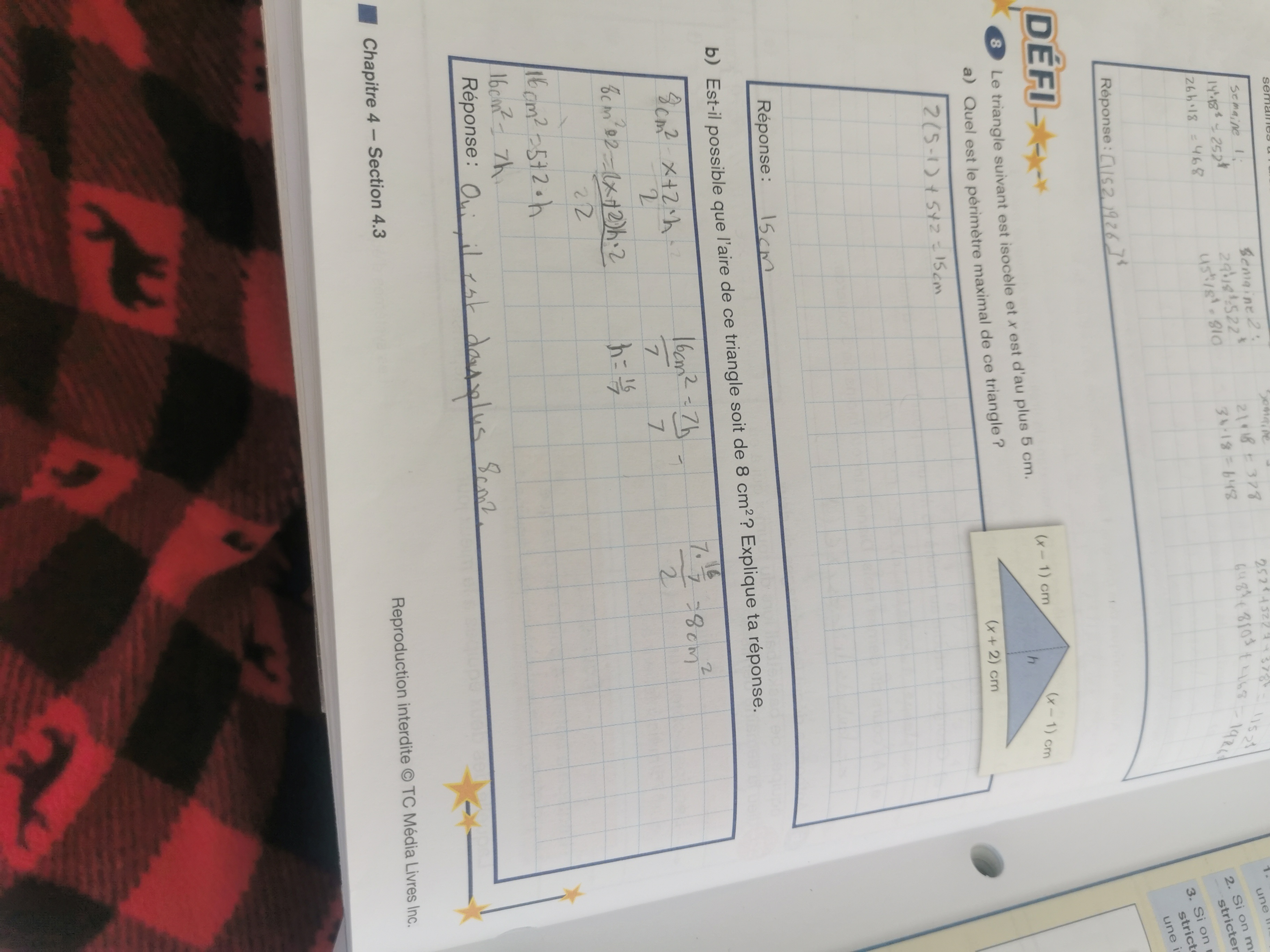
Dans le numéro 8b j'ai fait le numéro plusieurs fois avec plusieurs personnes et nous avons tous le même résultat alors que sur mon corrigé la réponse est que non, l'aire du triangle est d'au plus 6,79cm2. Je ne comprenais pas

LoutrePhilosophe7758

Vous avez trouver la hauteur d'un triangle lorsque l'aire = 8 cm^2 avec une base de 7 (Le maximum). Par contre, est-ce que cette base et hauteur correspondent au mesure de coté? Vous connaissez la longueur maximum des deux autres coté. Ils doivent être de (x-1), donc un maximum de 4 cm. Avec la hauteur d'un triangle 8 cm^2, vous pouvez trouver la longueur des cotés mimimum avec la Racine (3,5^2 + 16/7^2) = 4,18 cm, ce qui est plus haut que votre maximum (x-1). Pour avoir une aire de 8 cm^2, le triangle doit avoir une base de 7, une hauteur de 16/7 ET des cotés des 4,18 cm.

Comme les cotés auront une longueur supérieur au maximum, il est impossible d'avoir une aire d'au moins 8 cm^2.

Une autre façon de trouver est par le maximum des deux coté. (surement la méthode du corrigé)

Le maximum de la hauteur est 3,5^2(max de la base) + h^2(max hautreur) = 4^2 (max d'un côté)

Après calcul, on trouve que la hauteur maximum possible est 1,94 cm. On peut maintenant calculer l'aire maximale. (7 * 1,94)/2 = 6,79 cm^2. Voilà