Secondaire 5 • 3a
Bonjour!
Je n’arrive pas à faire la méthode de réduction avec ce système d’équations pouvez-vous me montrer comment le faire? ( Normalement je sais comment faire la méthode réduction mais il y a deux variable différentes et ça me mélange!) Merci!
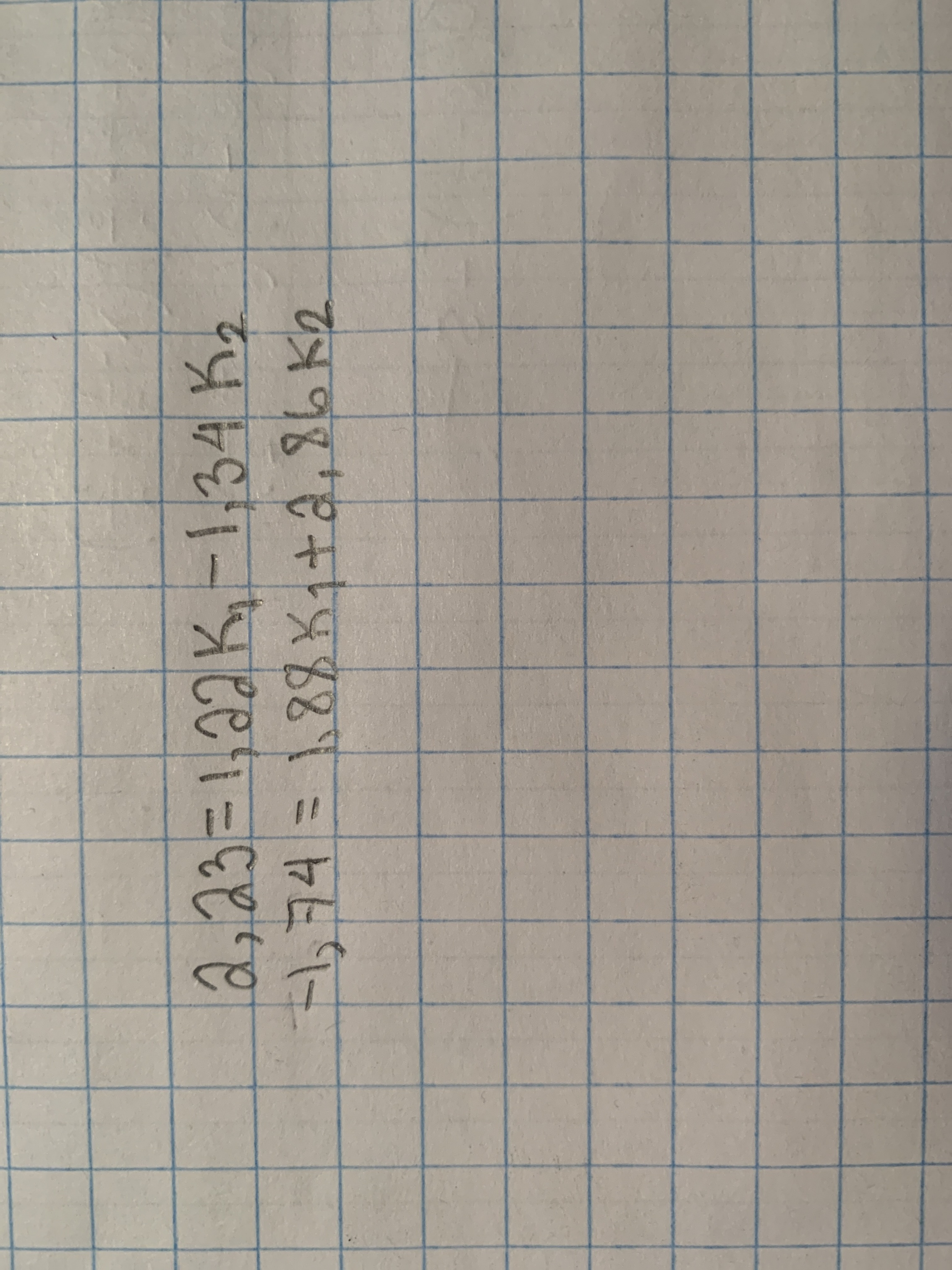






bonjour Ananas,
Il y a toujours 2 variables quand on utilise la méthode de réduction !
Tu pourrais renommer les variables x et y si cela t'aide.
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Salut !
Il y a plusieurs façons de procéder. Tu pourrais identifier une des deux variables, par exemple \(k_1\) et diviser la première équation par le coefficient de \(k_1\) dans cette première équation et diviser la deuxième équation par le coefficient de \(k_1\) dans la deuxième équation.
Ex : \begin{align*}2,\!23 &= 1,\!22k_1 - 1,\!34 k_2 \\ \\ -1,\!74 &=1,\!88k_1 + 2,\!86k_2\end{align*} devient \begin{align*}\frac{2,\!23}{1,\!22} &= \frac{1,\!22k_1 - 1,\!34 k_2}{1,\!22} \\ \\ \frac{-1,\!74}{1,\!88} &=\frac{1,\!88k_1 + 2,\!86k_2}{1,\!88}\end{align*}ce qui fait \begin{align*}1,\!8279 &\approx k_1 - 1,0984k_2 \\ \\ -0,\!9255 &\approx k_1 + 1,\!5213k_2\end{align*}
Si tu soustrais ensuite l'une de l'autre, par exemple si tu soustrais la deuxième de la première, \[1,\!8279-(-0,\!9255) \approx k_1 - k_1 -1,\!0984k_2 - 1,\!5213k_2\]ce qui fait \[2,\!7534 \approx -2,\!6197k_2\] \[\frac{2,\!7534}{-2,\!6197}\approx k_2\] \[-1,\!0510 \approx k_2\]
Et là tu peux trouver la valeur de \(k_1\) soit avec de la substitution, soit en utilisant une stratégie semblable (ex : diviser la première équation par \(-1,\!34\) et la deuxième par \(2,\!86\)).
Bon succès !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!