Secondaire 3 • 2a
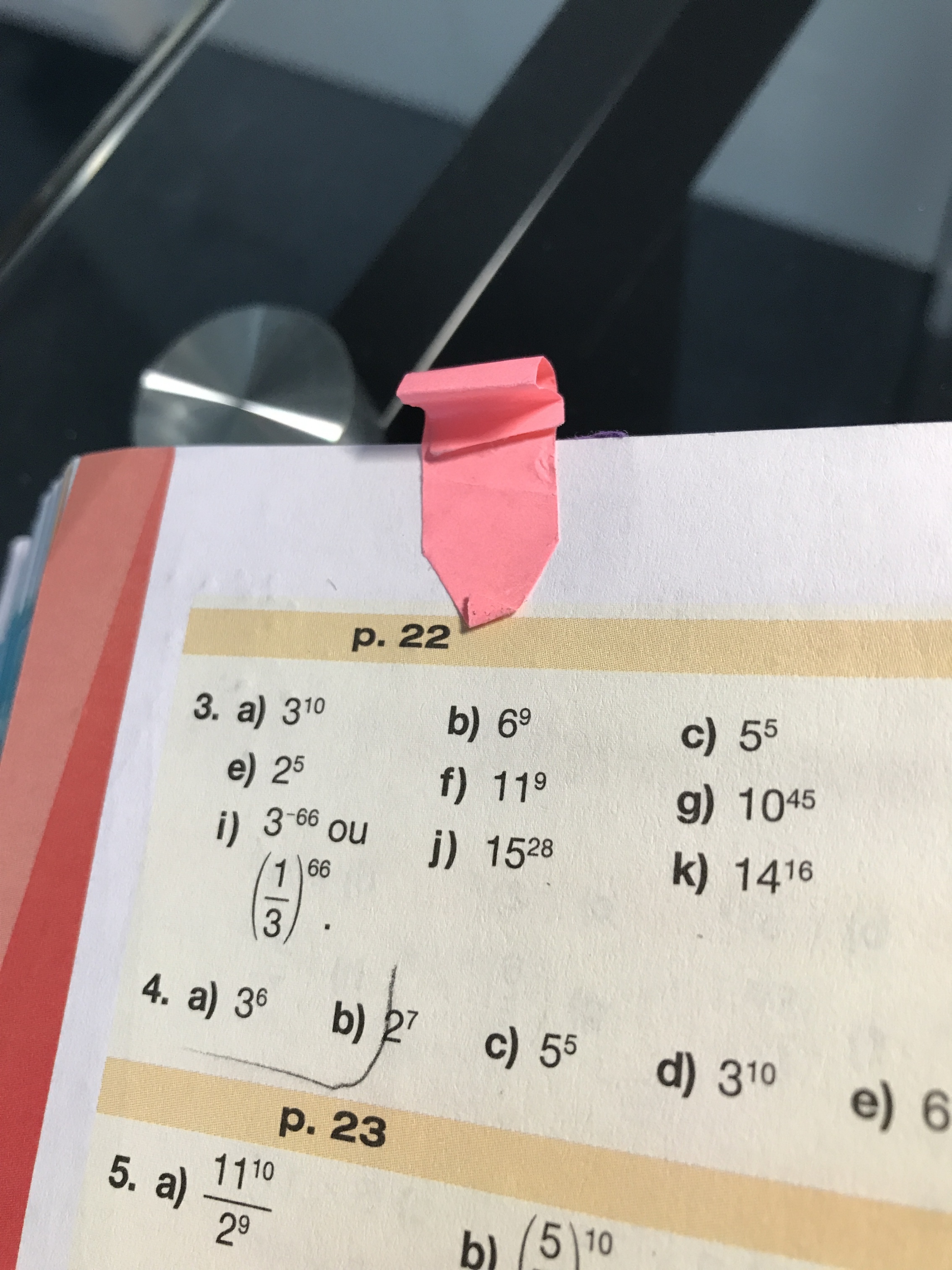
Je ne comprends pas la question 4 de la page 22. Au numéros A) 27 exposant 2 , je ne comprends pas quoi fait dans ce numéros? J’aimerais bien que une personne explique c’est quoi faut faire à ce numéros 4 ? La question que il faut faire c’est Récrivez chaque expression sous la forme d’une puissance de la plus petite base possible.
Là j’ai trouver une partir que j’ai trouvé 3 parce que j’ai fais 3 fois 9 égale 27 . J’ai pris 3 dans équation . 3 est la puissance .
J’essaye de trouver exposant 10 dans le numéros A) Comment il ont fais pour trouver 10 exposant dans le corriger ?

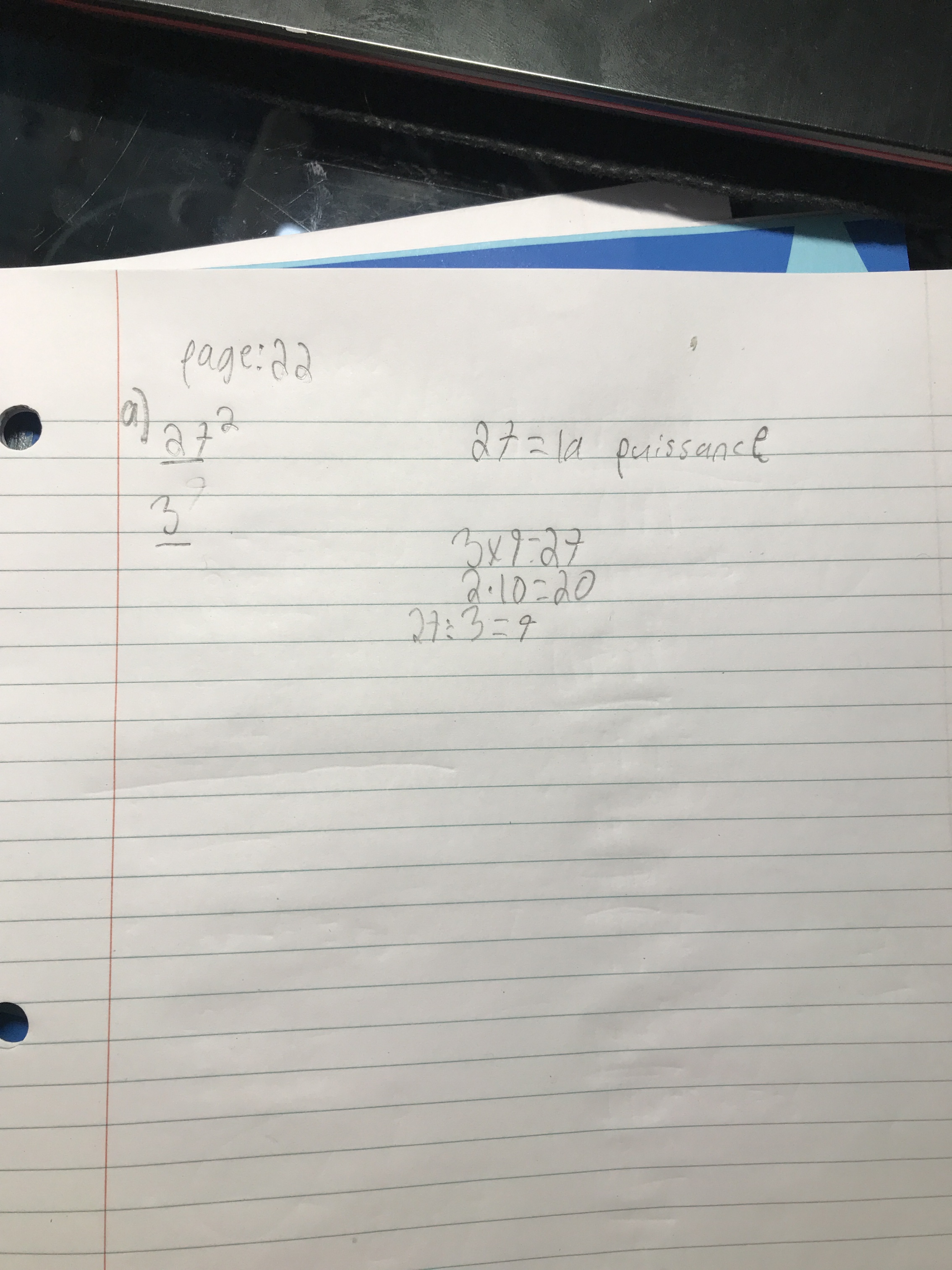






bonjour,
Suite à la réponse d'Éveline:
Pour savoir Quel nombre avec quel exposant donne 8
on peut factoriser 8.
Or 8 = 2×2×2 = 2³.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour Caribou Admirable!
Merci de faire appel à nos services 😉
Dans ce numéro, la clé est d'essayer de voir la base comme une puissance. À l'exercice a), on doit donc voir 27 comme une puissance et se demander Quel nombre avec quel exposant donne 27?
Faisons un exemple avec l'expression \( 8^4 \). On peut alors se poser la question Quel nombre avec quel exposant donne 8? Ici, on sait que \( 8 = 2^3 \). On peut donc remplacer 8 dans l'expression, comme ceci:
$$ 8^4 = (2^3)^4 $$
Ensuite, avec les lois des exposants, on peut multiplier les exposants pour obtenir la réponse finale:
$$ (2^3)^4 = 2^{3\times 4} = 2^{12} $$
Pour réviser les lois des exposants, tu peux consulter la fiche explicative suivante:
J'espère que cela t'aidera! N'hésite pas à nous réécrire!
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!