Secondaire 5 • 2a
Bonjour, j'ai des problèmes avec se problèmes de math 5 ts ou sn et j'aimerais savoir comment réussir à le résoudre.
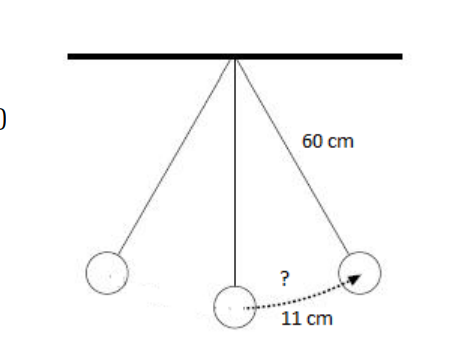
Un pendule de 60 cm de long effectue 10 oscillations en 25 secondes. Son amplitude (distance maximale à son point d’équilibre) est de 11 cm. Quelle est la distance qui le sépare de son point d’équilibre après 23 secondes.






bonjour,
La valeur de b dépend de la période mais b n'est pas la période.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut !
Tu peux exprimer la situation comme une fonction sinusoïdale. Il s'agira de la distance (y) à son point d'équilibre en fonction du temps (s). Cette fiche pourra t'aider à trouver la règle de la fonction :
La fonction aura cette forme :
$$ y=a\sin (b(x-h))+k $$
\(h\) et \(k\) représente le point d'origine de l'oscillation. Pour te simplifier la tâche, tu peux leur donner une valeur de 0. \(a\) représente l'amplitude de la fonction et \(b\) sa période. Je t'invite à visiter cette fiche pour la théorie et plus d'explication :
Je te laisse essayer par toi-même et si tu as d'autres questions, n'hésite pas !
fait -2 autant au cm que pour les oscillation tu va voir sa devrait fonctionner bonne chance tu est cabable
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!