Bonjour,
j’ai un devoir de mathématiques concernant les paramètres a,b,h et k. Ce devoir illustre un graphique, où il est tracé deux coube (fonction); une courbe représentant la fonction de base et une autre, celle transformée. Sur chaque courbe (base et transformée), il y’a un point qui correspond à la fonction opposée. A partir de ces information je doit trouver la valeur que représente les paramètres a, b, h et k de la fonction transformée. Pour le h et le k, je ne confronte aucun problème face à cela puisqu’il faut juste se référer au sommet de la fonction transformée. Cependant pour le a et le b, la situation m’est délicate. Je ne sais pas comment analyser le graphique et les calculs requis afin que je parvienne à trouver les «valeurs» celle-ci.
merci d’avance.
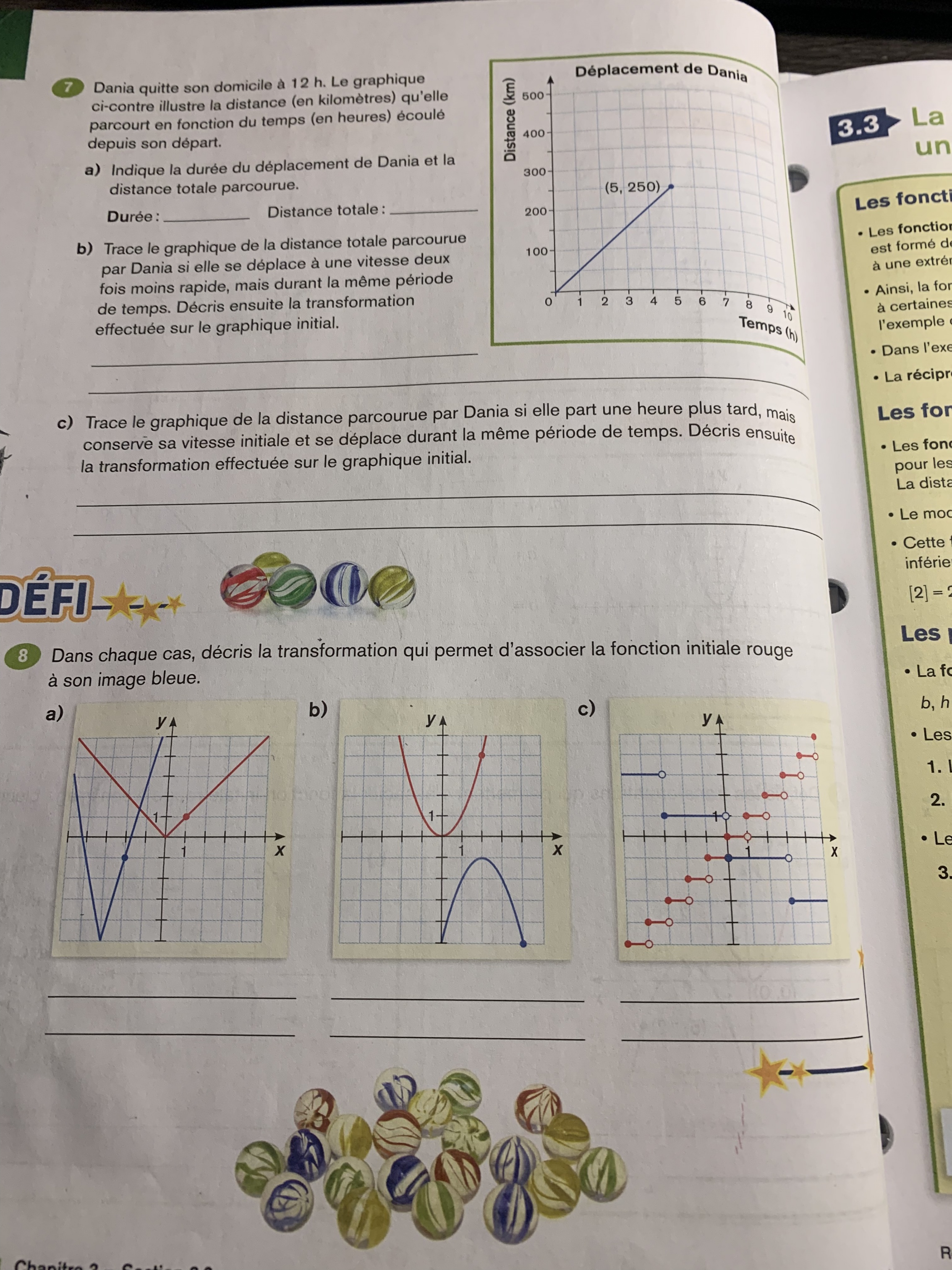
*le numéro 8 de la photo jointe est celui que je vise






bonjour,
Peu importe le type de fonction, on a :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
cf. https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-role-des-parametres-a-b-h-et-k-d-une-foncti-m1450
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut SourisSarcelle2105,
Merci pour ta question!
Pour trouver les fonctions transformées, le truc est de débuter avec la forme transformée de la fonction et d'ajouter les variables au fur et à mesure que l'on analyse le graphique.
Je vais faire le b en exemple pour te donner une idée de la démarche. Tu n'auras qu'à appliquer cette démarche pour les autres lettres afin de trouver les bonnes fonctions.
D'abord, identifions la forme transformée de notre fonction, il en existe trois types:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Dans notre cas, on connait le sommet, il est alors plus simple de travailler avec la forme canonique. Si on remplace les valeurs du sommet (2,-1) dans notre fonction, on obtient ceci:
$$y=a(x-2)^2-1$$
Dans cette fonction, il nous reste que le paramètre a à identifier. Si on remplace x et y par une coordonnée (4,-5) de la fonction on arrive à ceci:
$$-5=a(4-2)^2-1$$
Il ne reste plus qu'à isoler le paramètre a pour obtenir la fonction transformée.
L'approche est la même pour les deux autres fonctions, mais il y a quelques variations. En a, je te conseille d'utiliser cette forme transformée de la fonction valeur absolue:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
La fonction à trois paramètres est beaucoup plus facile à utiliser dans ce contexte que celle avec a et b.
Finalement, pour la lettre c, tu peux trouver la valeur de b directement sur le graphique. Une fois cette valeur trouvée et le sommet identifié, tu as uniquement a comme inconnu!
Voici une fiche sur la fonction escalier si tu as de la difficulté à identifier le paramètre b:
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!
Anthony B.
Salut!
Tu as beaucoup de paramètre pour les fonctions, mais la résolution reste la même.
1- Trouver le déplacement des point horizontalement ou verticalement, il faut prendre un point qui est facile à voir comme le points (0,0) de la figure a) et b). Tu calcules le déplacement avec point_final_x - point_initial_x et tu fas la même chose avec les Y.
2- Calculer la différence dans la courbure/ouverture, tu dois recalculer (différence en Y)/(différence en X) en gardant en tête le graphe de la fonction. Pour les fonctions non-linéaires, tu peux prendre la formule générale (y=x^2, y=|x|, ...) et calculer à l'aide des 2 points les constantes qui te restent à trouver.
Remarques:
Si le graphe fait une réflexion sur l'axe des Y, il y a un - sur le coéfficient de Y.
Tu peux aussi essayer plusieurs combinaisons pour en apprendre plus avec ce site:
https://www.desmos.com/calculator?lang=fr
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!