Secondaire 5 • 2a
Je ne comprends pas comment la réponse est
] - l’infini, -6] même si j’ai fait le graphique de cette fonction, car j’arrive à x=-6 pour cette inéquation donc c’est vraiment le schéma qui mène à cette réponse que je comprends pas et comment arriver à cette réponse






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut :D
La réponse de LoutreSolidaire8177 est très bonne! :)
Si tu souhaites en apprendre plus sur cette fonction ou simplement réviser quelques notions, c'est ici.
Bon exercice :) À ta prochaine question! :D
Salut,
Tu as fait le schéma et tu as résolu l'équation ? C'est une excellente stratégie !
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
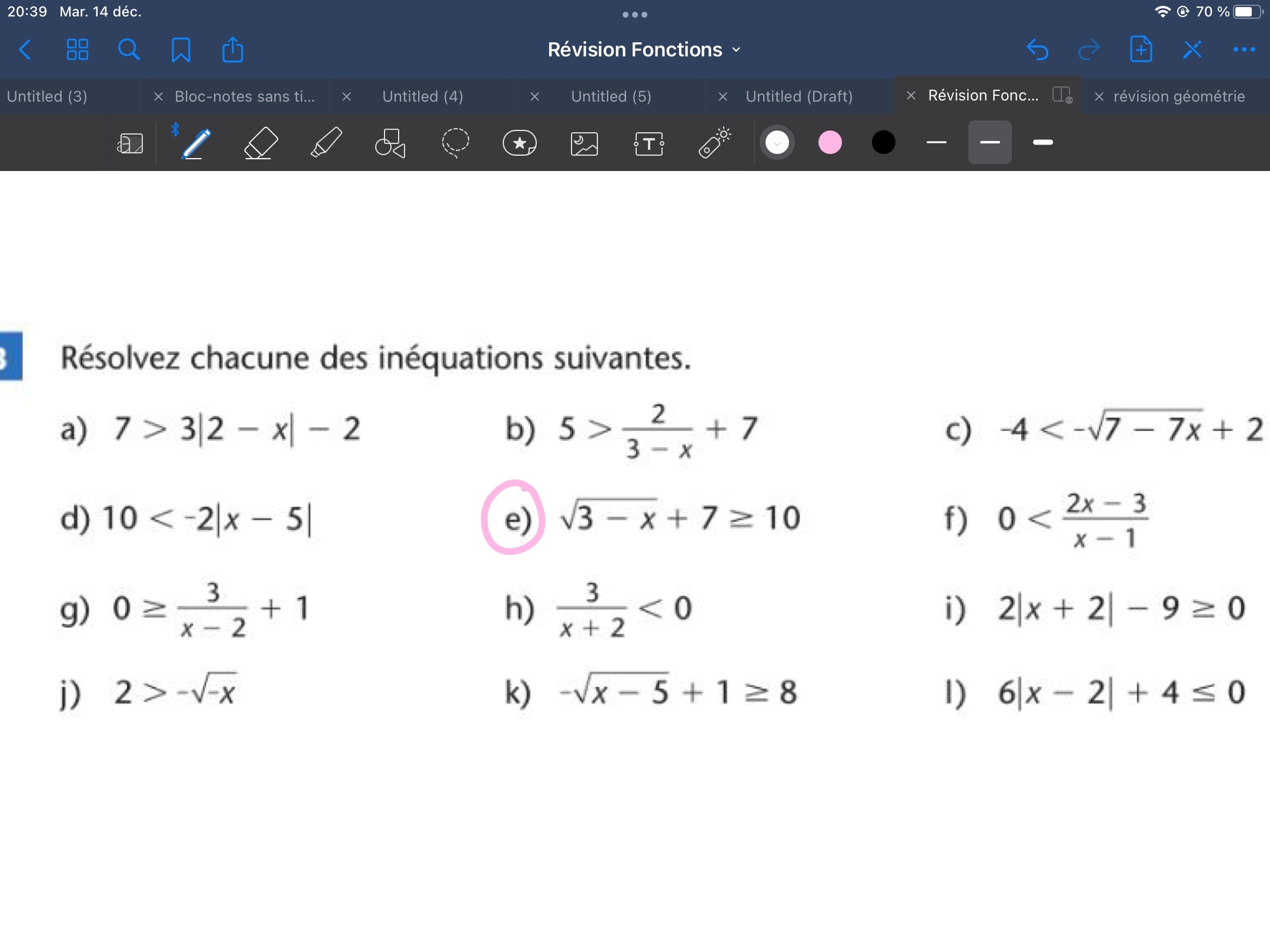
et \begin{align*}\sqrt{3-x} +7 &= 10 \\ \\ \sqrt{3-x} &= 3 \\ \\ 3-x &= 9 \\ \\ -x &= 6 \\ \\ x &= -6\end{align*}
On voit que la fonction racine carrée (en bleu) est au dessus de la droite d'équation \(y = 10\) (en rouge) avant \(x = -6\) (à gauche de \(x =-6\)). Puisque le symbole est \(\geq\) et non \(>\), on inclut la valeur \(-6\) dans l'ensemble solution. On obtient \[x \in \left]-\infty, \, -6\right]\]
Si tu y vas purement algébriquement, c'est possible. Cela se fait relativement bien car la fonction racine carrée est strictement croissante ou strictement décroissante sur son domaine. N'oublie pas la restriction : le radicande doit être positif \[3-x \geq 0\] \[-x \geq -3\]Lorsqu'on divise (ou multiplie) les membres d'une inéquation par un nombre négatif, on doit inverse le sens du symbole \(\geq\). On obtient \[x \leq 3\]Ensuite on résout \[\sqrt{3-x}+7 \geq 10\]On soustrait \(7\).\[\sqrt{3-x} \geq 3\]Puisque la racine carrée est positive, on élève au carré \[3-x \geq 9\] On soustrait \(3\) \[-x \geq 6\]On divise par \(-1\). On obtient \[x\leq -6\]ce qui concorde avec ce qu'on avait obtenu graphiquement (et les nombres inférieurs ou égal à \(-6\) sont de toute façon inférieurs ou égal à \(-3\) et cela respecte la restriction).
En espérant avoir répondu à ta question !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!