Secondaire 5 • 4a
Salut,
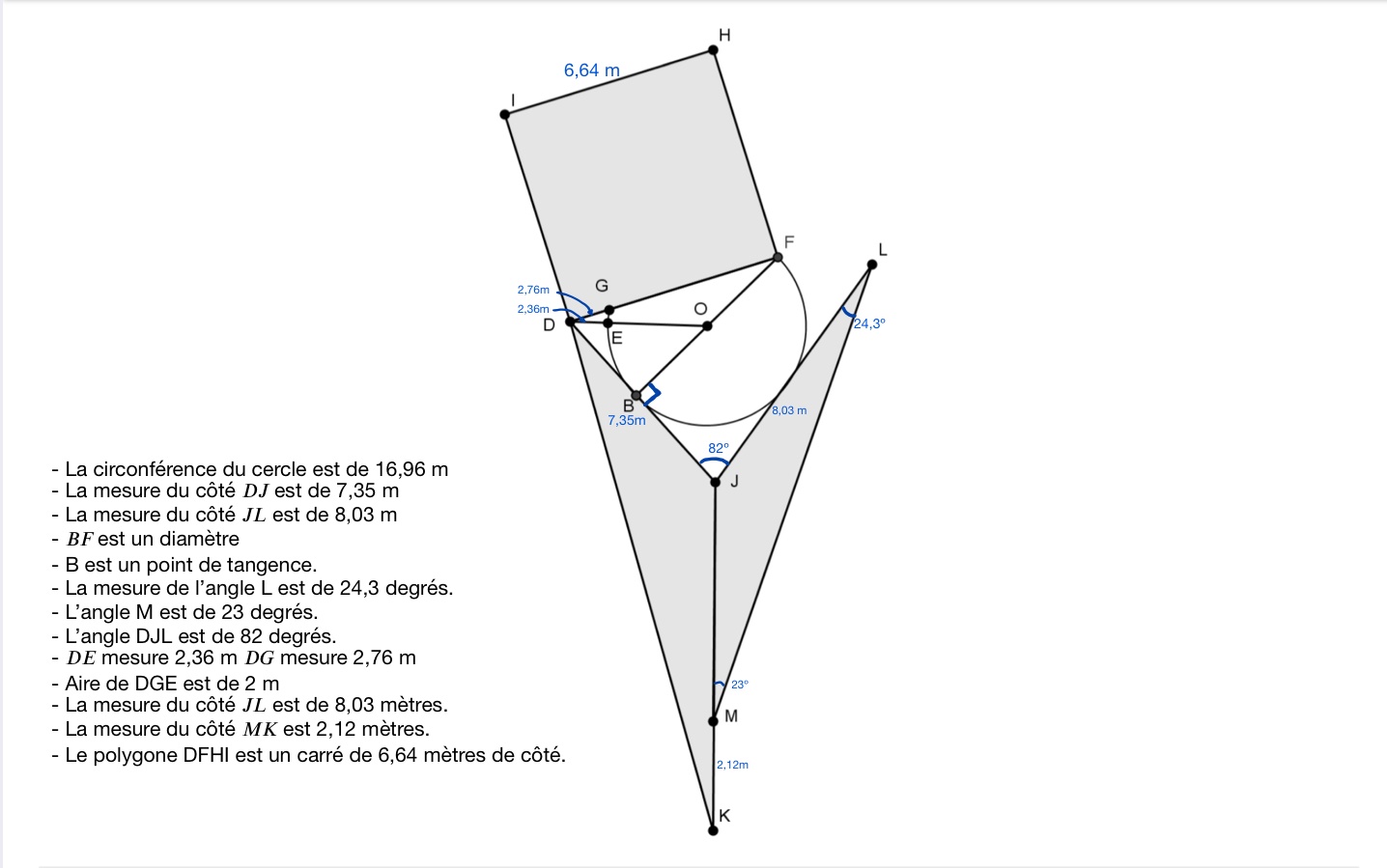
Je fait des exercices sur les relations métriques dans le cercle et j'ai de la difficulté avec ce problème. À l'aide des contraintes à respecter, je dois calculer l'aire totale du logo (les deux triangles, le carré et la partie visible du cercle). J'ai trouvé l'air des triangles et du carré, mais je n'arrive à trouver l'aire du cercle. Pouvez-vous m'expliquer comment je dois m'y prendre.
merci






bonjour,
Comme le mentionne Katia, il y a d'autres démarches possibles.
Ainsi pour calculer l'aire de la partie visible du cercle, on additionne:
Note: La formule de Héron et la formule trigonométrique peuvent être utiles.
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-perimetre-et-l-aire-des-triangles-m1201
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
La formule d'aire d'un disque est :
A = π x r²
Pour trouver le rayon du cercle, tu peux utiliser la mesure de la circonférence fournie. Puisque la circonférence d'un cercle ce trouve grâce à la formule : C = 2πr, tu peux isoler la variable r. Puis, tu seras en mesure de trouver l'aire du disque.
Ensuite, nous voulons soustraire de cette aire l'aire de la partie du cercle empiétant sur le carré. On devra d'abord trouver l'aire du secteur, puis y soustraire l'aire du triangle GFO. On devra utiliser la formule suivante :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On cherche l'aire du secteur, on connait l'aire du disque, et on devra trouver l'angle au centre, soit celui-ci :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour ce faire, puisqu'on connait la mesure de OF (le rayon), de OG (le rayon), et on peut déterminer celle de GF (DF-DG), on peut utiliser la loi des cosinus dans le triangle FGO pour trouver l'angle GOF. Une fois trouvé, on sera en mesure de trouver l'aire du secteur formé par les segments GO, OF et l'arc intercepté par les points G et F (l'aire du secteur illustré ci-dessous en bleu), et ce à l'aide de la formule précédente.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici une fiche sur la loi des cosinus qui pourrait t'être utile :
https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-loi-des-cosinus-m1294
Maintenant, il faut soustraire de l'aire du secteur bleu l'aire du triangle GFO (en vert), puisque l'on souhaite trouver uniquement l'aire de la partie du cercle sur le carré (en jaune) :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour trouver l'aire du triangle vert, tu dois d'abord trouver une des hauteurs du cercle. Je te conseille de trouver la hauteur issue du sommet O à l'aide du théorème de Pythagore. (Tu auras besoin du rayon et de la demi-mesure de GF). Puis, tu devras utiliser la formule d'aire d'un triangle, soit A = base x hauteur /2
Voilà! Il existe probablement des démarches alternatives, donc ne t'inquiète pas si tu n'avais pas pensé à faire exactement la même chose! ;)
Voici des fiches qui pourront t'être utiles :
Si tu as d'autres questions, n'hésite pas :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!