Secondaire 4 • 2a
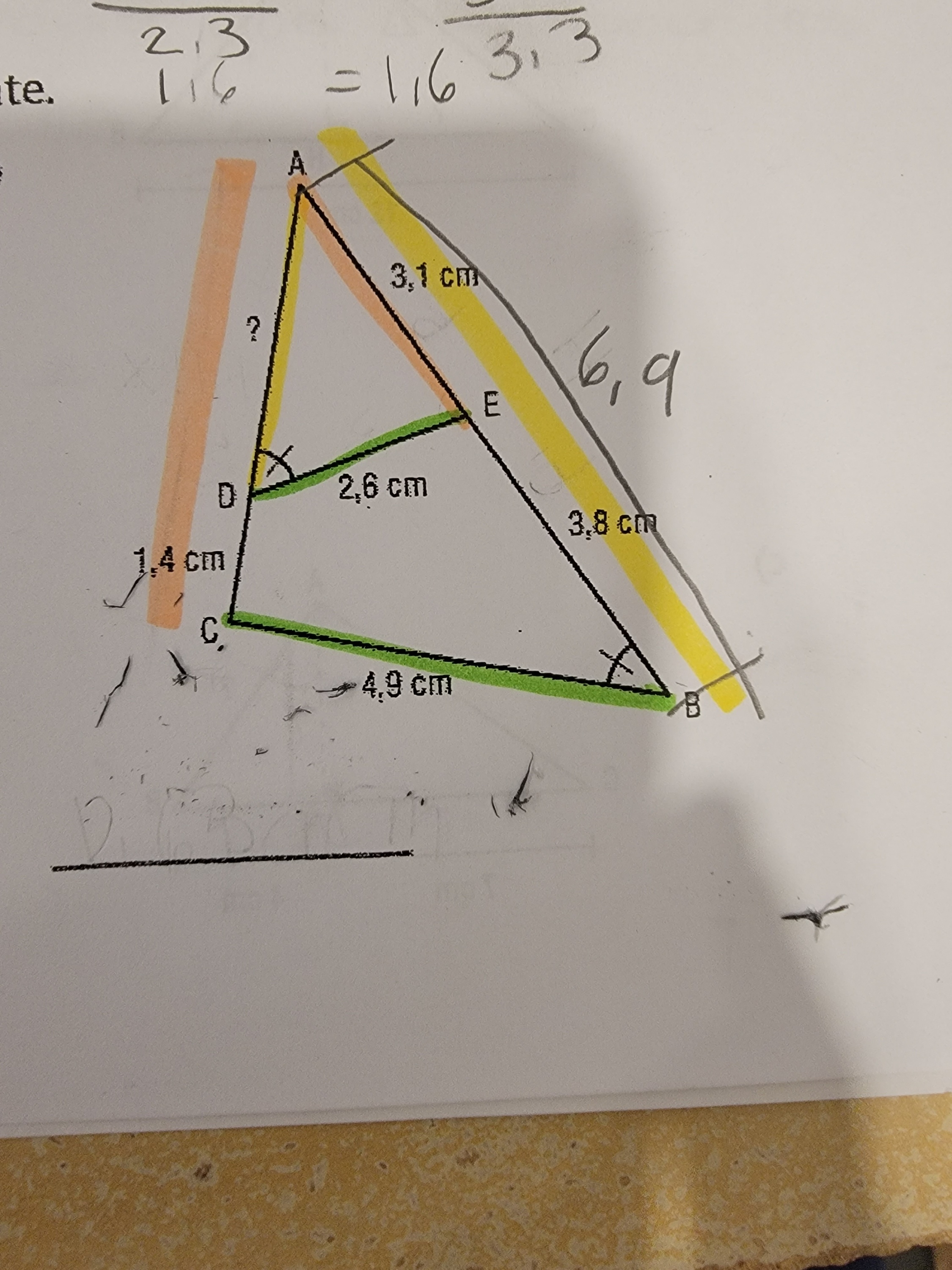
Bonjour, ça fait plusieurs fois que je fais ce numéro mais je n'arrive jamais à la bonne réponse. Est-ce que vous pouvez m'aider? Il faut trouver la mesure manquante.
Merci d'avance :)






Bonjour Lune Calme!
Merci de faire appel à nos services 😉
La démarche décrite par ton collègue est pertinente!
On peut aussi procéder en cherchant directement à connaître la valeur inconnue. On utilise donc un rapport qui compare les côtés verts et les côtés jaunes, comme ceci:
$$ \frac{mAD}{6,9} = \frac{2,6}{4,9} $$
Toutefois, ici ce sont les mesures du triangle qui sont erronées, puisque les deux méthodes valides donnent des résultats différents!
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Bonjour LuneCalme3802,
Merci pour ta question ! On va regarder ça ensemble :)
Alors d'abord, bravo, tu as bien identifié tes côtés correspondants de tes deux triangles semblables.
(As-tu besoin de prouver que ces triangles sont semblables?)
Si oui : On a deux triangles semblables par A-A-A
Angle ABC isométrique à Angle ADE (donné)
Angle CAB isométrique à Angle DAE (angle commun)
Angle BCA isométrique à Angle AED (somme des angles intérieures d'un triangle est 180 degrés)
Maintenant que cela est fait, on doit trouver notre rapport des mesures.
On connait nos mesures de côtés verts et on cherche la mesure du petit côté orange (rose?)
2,6/4,9 = 3,1/x
Ainsi, x = 5,8 cm
Il ne nous manque plus qu'à enlever le 1,4 cm donné du 5,8 cm.
On obtient ainsi ? = 5,8 - 1,4 = 4,4 cm
J'espère que ça t'aide :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!