Secondaire 5 • 3a
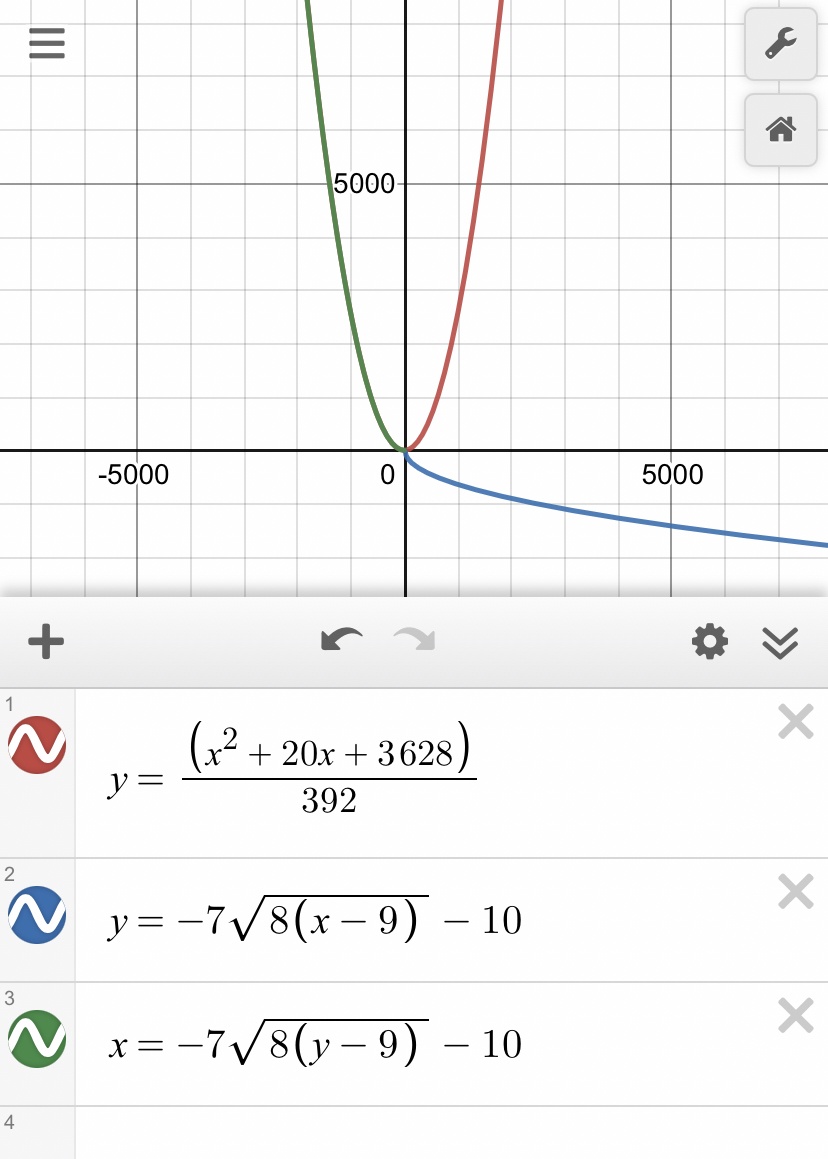
J’ai dessiné la réciproque de la fonction sur desmos. Je crois que c’est la réponse numéro 2, mais je ne suis pas certains de comprendre les symbole pour décrire le domaine et l’image.
Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
La réponse est bien le 2e choix. Pour y arriver, il fallait trouver le domaine et l'image de ta fonction de base, puis inverser ce domaine et cette image pour trouver ceux de la réciproque.
Dans le graphique ci-dessous, j'ai tracé la fonction de base. Nous pouvons constater que le domaine est de 9 à l'infini, c'est-à-dire que la variable x peut prendre des valeurs entre x = 9 et plus. En d'autres mots, dom g = [9, ∞ [, ou encore x ≥ 9.
L'image est de -10 à moins l'infini, donc ima g = [-10, -∞[, ou encore y ≤ -10.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puisque, la réciproque d'une fonction est une relation où le domaine et l'image sont inversés, nous avons donc :
ima g^−1 = [9, ∞ [, ou encore y ≥ 9
dom g^-1 = [-10, -∞[, ou encore x ≤ -10
Ce n'était donc pas nécessaire de tracer le graphique de la réciproque, celui de la fonction de base suffisait.
Voici une fiche sur la réciproque d'une fonction pour plus de détails sur cette notion : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-reciproque-d-une-fonction-m1110
Et en voici une sur le domaine et l'image :https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/les-proprietes-des-fonctions-m1107
N'hésite pas à nous réécrire si tu as d'autres questions :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!