Zone d’entraide

RubisTurquoise4719

Bonjour,

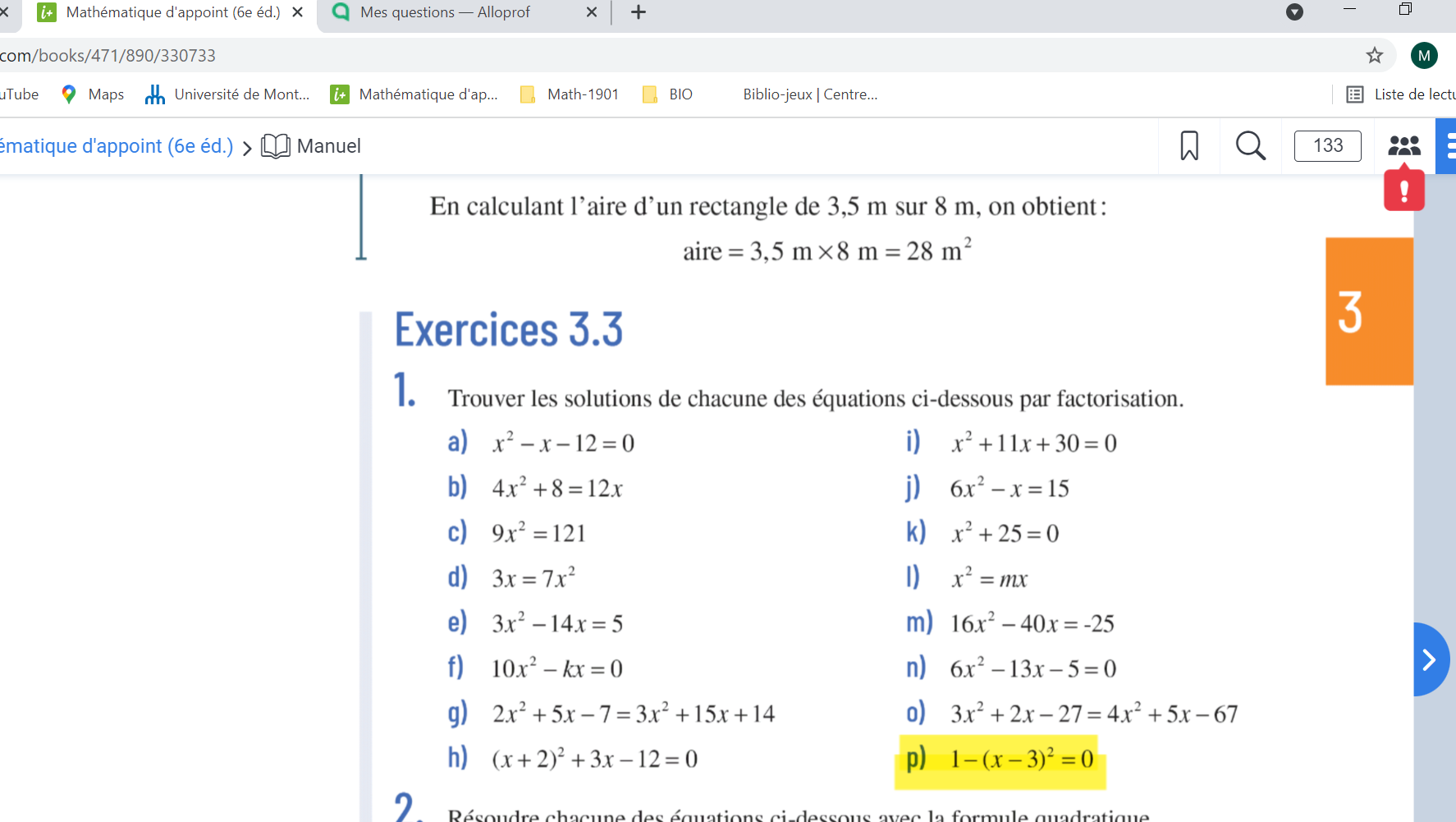
je dois trouver les solutions de chacune des équations ci-dessous par factorisation (équation de second degré). J'ai un blocage pour le P. La réponse est 2 et 4 mais je n'y arrive pas!

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

AvocatTenace6777

bonjour ,

Si $\sqrt{1}=\pm 1$

alors $f(x)=\sqrt{x}$ n'est pas une fonction !

AvocatTenace6777

bonjour Rubis,

On aurait pu factoriser la différence de carrés

$$1-(x-3{)}^2=0$$

$$(1+(x-3))(1-(x-3))=0$$

$$(x-2)(4-x)=0$$

De là, les solutions.

Katia K

Salut!

Je pense que tu as simplement oublié d'écrire la réponse négative lorsque tu as effectué la racine carrée de 1. Recommençons ensemble du début. Nous avons :

$$1-(x-3{)}^2=0$$

Nous allons commencer par déplacer la constante 1 d'un côté et la variable de l'autre, comme ceci :

$$(x-3{)}^2=1$$

Nous allons maintenant faire l'opération inverse d'un exposant 2, soit une racine carrée, et ce de chaque côté de l'équation :

$$\sqrt{(x-3{)}^2}=\sqrt{1}$$

$$x-3=\sqrt{1}$$

En effectuant la racine carrée de 1, il ne faut pas oublier d'écrire la valeur négative!

$$x-3=\pm 1$$

Il ne reste plus qu'à déplacer la constante -3 de l'autre côté de l'équation pour isoler la variable x. Nous avons au final :

$$x-3+3=\pm 1+3$$

c'est-à-dire :

$$x=1+3=4$$ et $$x=-1+3=2$$

Voilà! N'hésite pas à nous réécrire si tu as d'autres questions :)