Secondaire 5 • 3a
Bonjour,
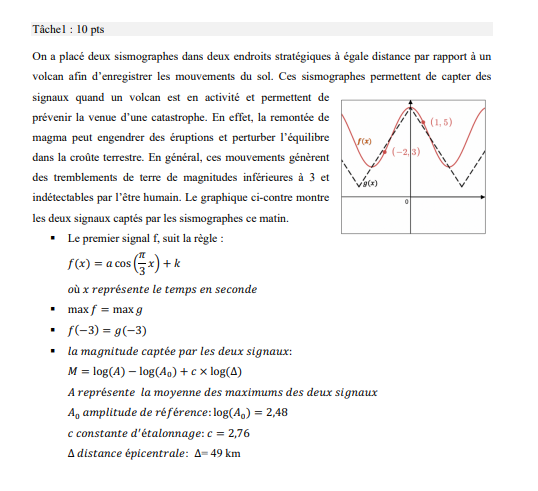
Je n'arrive pas a trouver le maximum de la fonction cosinus. Je pense que le h = -3 et que k = -6 mais je ne suis pas sûre. J'ai essayé de trouver l'amplitude mais je n'y arrive pas.
Merci pour votre aide!






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour,
Tu peux te référer à l'explication de ton/ta collègue!
Pour la compléter, je tiens juste à te rappeler de la théorie, de la forme générale d'une fonction cosinus.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Selon ton énoncé, tu as en effet déjà ton h.
Il ne te reste qu'à trouver la valeur de a et de k. Tu peux faire cela à l'aide des deux points donnés par le graphique en remplaçant x et y dans l'équation. Tu auras donc deux équations.
Grâce aux méthodes de résolution de systèmes linéaires, tu pourras trouver a et k.
Bonne soirée! N'hésite pas si tu as d'autres questions.
Salut !
On donne la règle de la fonction
\[f(x) = a\cos\left(\frac{\pi}{3}x\right) + k\]
La valeur de \(h\) est donc 0. On voit que le graphique possède un maximum en \(x = 0\) ce qui est cohérant. Pour les valeurs de \(a\) et de \(k\), tu peux remplacer \(x\) et \(f(x)\) deux fois par les coordonnées des couples \((-2, \, 3)\) et \((1, \, 5)\).
J'obtiens \begin{align*}3 &= a\cos\left(\frac{\pi}{3}(-2)\right) + k \\ \\ 5 &= a\cos\left(\frac{\pi}{3}(1)\right) + k\end{align*} Tu peux trouver les valeurs du cosinus dans le cercle trigonométrique.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
J'observe que
\[\cos\left(\frac{\pi}{3}(1)\right) = \cos\left(\frac{\pi}{3}\right) = \frac{1}{2}\]
et que puisque \[-\frac{2\pi}{3} + 2\pi = \frac{4\pi}{3}\]j'observe aussi que \[\cos\left(\frac{\pi}{3}(-2)\right) = \cos\left(-\frac{2\pi}{3}\right) = \cos\left(\frac{4\pi}{3}\right) = -\frac{1}{2}\]
Je peux donc remplacer.
\begin{align*}3 &= a\cos\left(-\frac{2\pi}{3}\right) + k \\ \\ 5 &= a\cos\left(\frac{\pi}{3}\right) + k\end{align*}
devient
\begin{align*}3 &= a \cdot \left(-\frac{1}{2}\right) + k \\ \\ 5 &= a \cdot \left(\frac{1}{2}\right) + k\end{align*}
ce qui fait
\begin{align*}3&= -\frac{1}{2}a + k \\ \\ 5&= \frac{1}{2}a + k\end{align*}
Tu peux déterminer les valeurs de \(a\) et de \(k\) en résolvant le système d'équations. Tu peux procéder par la méthode de ton choix (comparaison, substitution, réduction).
Avec les valeurs de \(a\) et \(k\), il te sera possible de continuer le problème.
Bon succès !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!