Zone d’entraide

PotassiumAgile5785

Merci Madame Katia :)

Mais je ne crois pas avoir bien compris. L'examen est demain, et je me demandais s'il serait possible que vous me partagiez votre démarche avec la réponse.

Je ne comprends surtout pas comment trouver le profit final.

Je ne sais pas si j'ai bien fait, mais j'ai obtenu qu'il n'a pas raison, puisque le profit maximal (les sommets entiers seulement) est de 123 750 $.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Merci!

Katia K

Salut!

Pas de problème, on est là pour t'aider :) Repartons du début.

Premièrement, identifions les variables :

x : nombre de tables du modèle A

y : nombre de tables du modèle B.

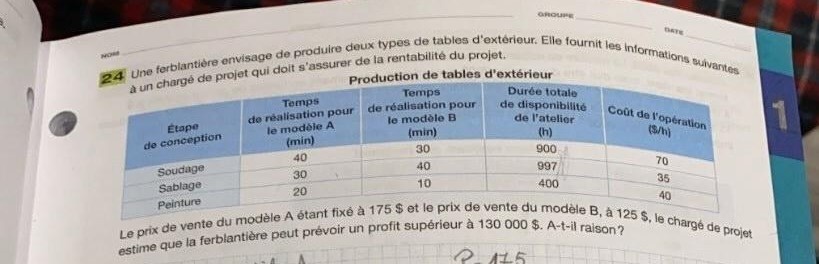
Nous allons maintenant traduire les contraintes de la situation par un système d'inéquations. Nous allons poser des inéquations pour chaque étape de conception, soit le soudage, le sablage et la peinture afin de maximiser le nombre de tables de chaque sorte pouvant être produites selon la durée de disponibilité de l'atelier pour chaque étape de conception :

Soudage : 40x + 30y ≤ 54 000

Sablage : 30x + 40y ≤ 59 820

Peinture : 20x + 10y ≤ 24 000

Toutes les valeurs sont en minutes. En effet, 900h = 54 000 min, 997h = 59 820 min, et 400h = 24 000. Tu aurais également pu à la place convertir les minutes en heures.

Les inéquations ci-dessus permettent ainsi de maximiser le nombre de tables de chaque modèle pouvant être produit pendant la contrainte de temps de disponibilité de l'atelier. En d'autres mots, notre but est de concevoir le plus de tables possible dans le laps de temps accordé afin d'amasser le plus grand profit possible.

Ensuite, il faut établir la règle de la fonction à optimiser. Puisque le but est de faire le plus grand profit possible, et que les tables de type A et de type B rapportent respectivement 175$ et 125$, nous avons la règle suivante :

$$P = 175x + 125y − (\frac{70}{60}(40x + 30y) + \frac{35}{60}(30x + 40y) + \frac{40}{60} (20x + 10y))$$

"175x + 125y" est le profit de vente des x tables de type A et des y tables de type B.

Le reste de l'équation représente le coût de chaque opération selon le nombre de tables. Ce coût est à déduire de notre profit de vente afin d'obtenir le profit final.

Par exemple, le soudage est une opération qui coûte 70$ par heure, donc (70/60)$ par minute (donc environ 1,17$/min, je l'ai écrit de la sorte pour bien détaillé la démarche pour qu'elle te soit le plus claire possible, mais tu peux directement remplacer les fractions en nombre décimal si tu le souhaites).

Ça prend 40 min faire 1 table de modèle A et 30 min faire 1 table de modèle B. Si nous concevons x tables A, alors cela prendra 40x minutes, et si nous concevons y tables B, cela prendra 30y minutes. Le temps total pour faire ces x et y tables serait donc (40x + 30y) minutes. Puisque cette opération coûte (70/60)$ par minute et qu'elle dure (40x + 30y) minutes, cela coutera donc ((70/60)•(40x + 30y)) $

J'ai fait la même chose pour les deux autres opérations. Au final, j'ai déduit du profit de vente le coût de chaque opération selon le nombre de tables x et y.

Rendus à cette étape, nous avons nos contraintes, soit :

40x + 30y ≤ 54 000

30x + 40y ≤ 59 820

20x + 10y ≤ 24 000

Et notre fonction à optimiser, soit :

$$P = 175x + 125y − (\frac{70}{60}(40x + 30y) + \frac{35}{60}(30x + 40y) + \frac{40}{60} (20x + 10y))$$

Que nous pouvons simplifier de la sorte :

$$P = 175x + 125y − \frac{1}{60}(70(40x + 30y) + 35(30x + 40y) + 40(20x + 10y))$$

$$P = 175x + 125y − \frac{1}{60}(2800x + 2100y + 1050x + 1400y + 800x + 400y)$$

$$P = 175x + 125y − \frac{1}{60}(4650x + 3900y)$$

$$P = 175x + 125y − (77,5x+ 65y)$$

$$P = 175x + 125y − 77,5x - 65y$$

$$P = 97,5x + 60y$$

Puis, il faut tracer le polygone de contrainte, soit :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

(PS: J'ai utilisé le logiciel Desmos pour tracer ce graphique, voici le lien du site : https://www.desmos.com/calculator?lang=fr)

Nous avons 2 sommets dans notre polygone de contraintes, soit (522,1104) et (900, 600). Il nous reste maintenant à évaluer la fonction à optimiser pour chacun de ces sommets.

Sommet (522,1104) :

$$P = 97,5(522) + 60(1104)$$

$$P = 117 135$ $$

Sommet (900, 600) :

$$P = 97,5(900) + 60(600)$$

$$P = 123 750$ $$

Puisque le profit le plus élevé est de 123 750$, nous trouvons donc qu'il faut 900 tables du modèle A et 600 tables du modèles B. Maintenant, pour répondre à la question finale, si le chargé de projet a raison ou non d'affirmer que nous pouvons excéder un profit de 130 000$, la réponse est non, il n'a pas raison, puisque nous avons trouvé que le profit maximum est de 123 750$ seulement, et 123 750 < 130 000$.

Donc tout ça pour dire que oui, tu as eu la bonne réponse, bravo!! :D

En espérant t'avoir aidé, je te souhaite un bon succès pour ton examen, je suis sûre que ça va super bien se passer :)