Secondaire 5 • 1m
Bonjour, il faut que je résous cette inéquation . Je ne comprend pas comment la réponse n’est pas impossible. J’obtiens tourjours une valeur absolue est égale à 0 à la fin. Ma prof nous a pas apprit les restrictions, elle veux qu’on fasse des graphiques à la place. Voilà l’inéquation et ma démarche:
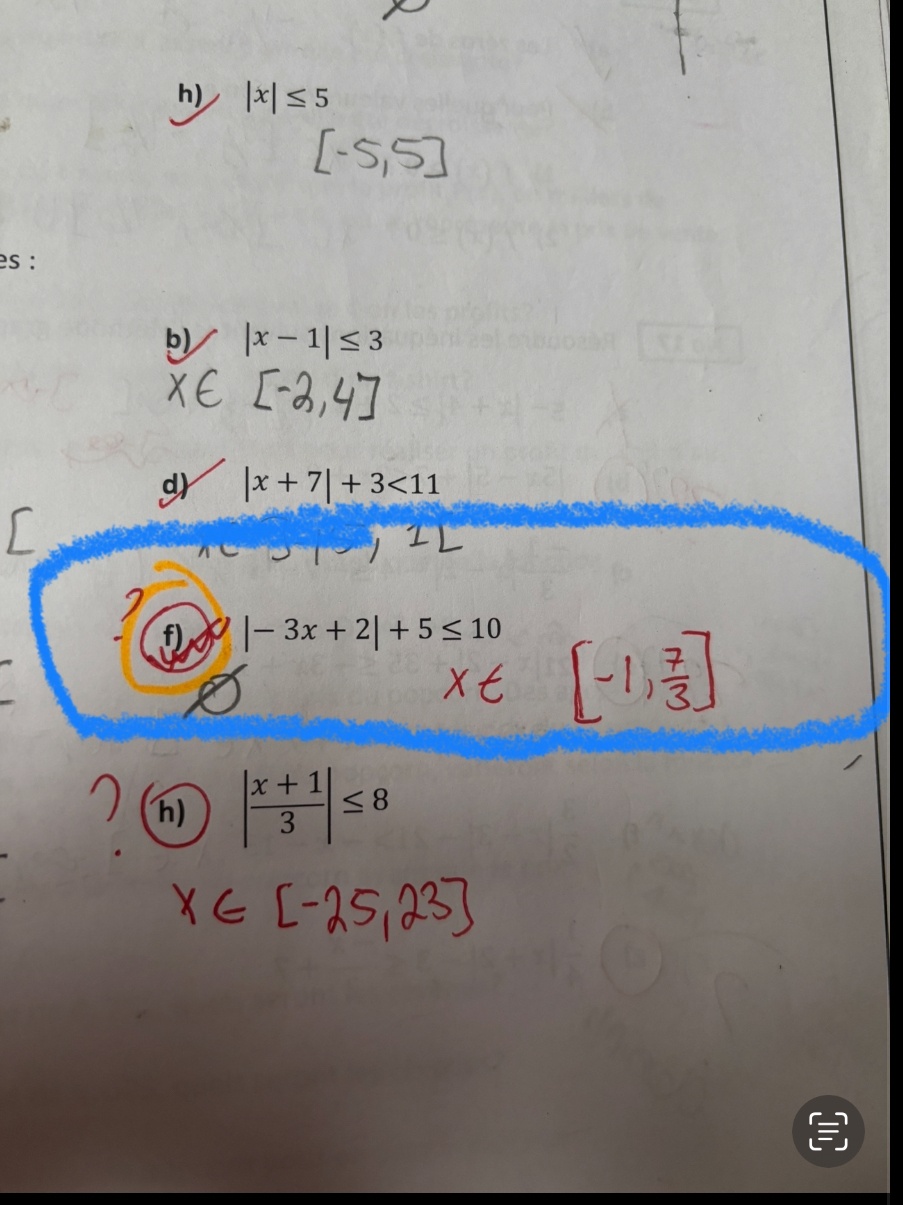
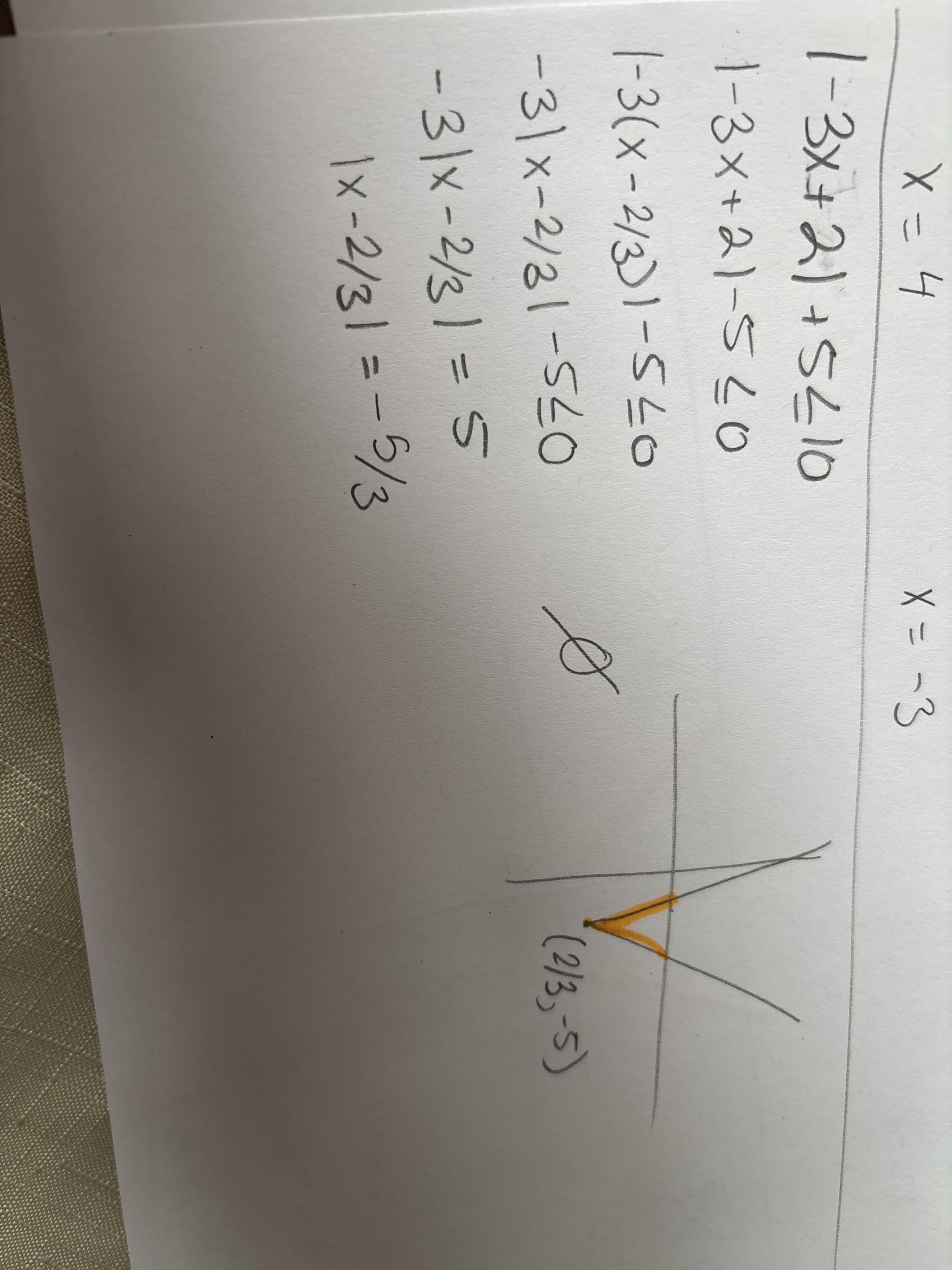






Et pour l'illustration:
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Voici comment je procède (méthode longue mais qui fonctionne toujours)
|-3x + 2| + 5 ≤ 10
|-3x + 2| ≤ 5
Premier cas -
l'intérieur de la valeur absolue est non négatif
=> -3x + 2 ≥ 0 ; -3x ≥ -2 ; 3x ≤ 2 (car en multipliant ou divisant par un nombre négatif on doit changer le sens de l'inégalité) ; x ≤ 2/3
et pour la valeur absolue -3x + 2 ≤ 5 ; -3x ≤ 3 ; 3x≥-3 ; x≥-1
au final dans le premier cas -1≤x≤2/3
Deuxième cas -
l'intérieur de la valeur absolue est négatif
=> -3x + 2 < 0 ; x > 2/3
et pour la valeur absolue -(-3x + 2) ≤ 5 (car la valeur absolue étant toujours non négative si l'intérieur est négatif on corrige avec le signe - en avant) ; 3x - 2 ≤5 ; 3x ≤7; x ≤ 7/3
au final dans le deuxième cas 2/3<x≤7/3
donc effectivement x appartient à [-1,7/3]
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!