Secondaire 5 • 1m
Bonjour, je n’arrive pas à comprendre si est ce que la pente d’une des demi-droite de la fonction valeur absolue est le paramètre a dans la forme canonique avec la présence du parametre b (f(x)=a|b(x-h)|+k ou est le paramètre à dans la forme ou il n ya PAS la présence du paramètre b (f(x)=a|x-h|+k). Il y a une exemple ci-dessous.






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour BleuetBionique2347,
Merci pour ta question :)
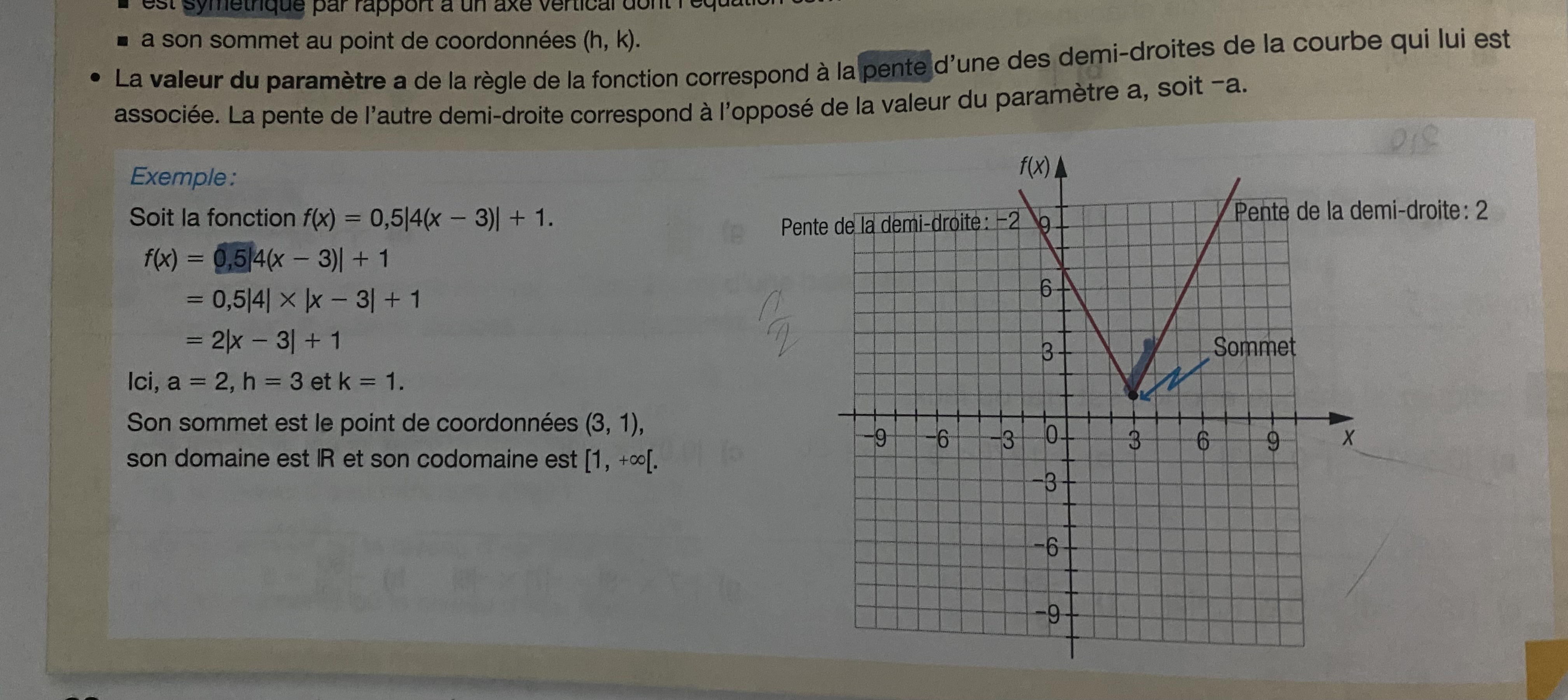
La pente d'une demi-droite de la fonction valeur absolue est égale à la multiplication du paramètre a et du paramètre b. Lorsque le paramètre b n'apparait pas dans l'équation, on suppose que sa valeur est 1. Cela explique pourquoi lorsque le paramètre b est absent de l'équation, la pente d'une demi-droite a la même valeur que le paramètre a (puisque que c'est l'équivalent de ax1=a).
Attention par contre, il faut déterminer le signe du paramètre a selon l'ouverture de la fonction (vers le haut ou vers le bas). Je te laisse un lien ici pour que tu puisses voir cela en exemple:
N'hésite pas si tu as d'autres questions :)
Sandrine
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!