Secondaire 3 • 1m
Nous avons eu trois examens de math cette semaine, et le dernier est aujourd'hui. Je n'ai pas révisé pour le premier, mais le deuxième j'ai passé la semaine à réviser pendant beaucoup de temps. J'ai dépensé beaucoup d'efforts, mais cela n'a pas payé. Les autres pensent que je suis une intello et pensent que ma pire note était 90 alors quand j'ai eu 66 à celui-ci malgré mes efforts, je me suis sentie trop nulle. De plus, je stresse pour l'examen d'aujourd'hui sur la multiplication de binômes, puisque je n'ai pas révisé. Je n'ai même pas réussi cette question et je ne comprends pas ce qu'il y aura à faire dans l'examen.
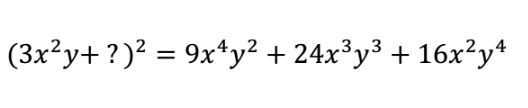






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Bonjour LoupSage3941,
Merci de faire appel à nos services! 🙂
Je comprends, c'est frustrant de passer du temps à étudier et voir que le résultat n'est pas celui qu'on espère. Peut-être que de petits trucs et astuces pourraient t'aider à mieux te préparer. Je t'invite à consulter le lien suivant pour trouver des stratégies qui pourraient t'aider: https://www.alloprof.qc.ca/fr/eleves/bv/exams-et-trucs/trucs-pour-etudier-t2000
Dans ton exercice, le plus facile serait d'enlever l'exposant et de placer les parenthèses côte à côte comme: (3x^2y+?)(3x^2y+?). Si tu suis tes règles de distributivité, tu remarqueras que le dernier terme 16x^2y^4 provient de la multiplication de ? et ?, autrement dit de ?^2. Si on pose l'équation 16x^2y^4=?^2, tu as la possibilité d'effectuer un calcul beaucoup plus simple pour trouver la réponse :)
Et tu sais, il n'y a rien comme la pratique! Alors je t'invite également à faire ces quelques exercices et à regarder la mini récup: https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/la-multiplication-d-expressions-algebriques-m1074
Allez, on ne lâche pas, tu peux réussir!!!
N’hésite pas à nous réécrire si tu as d’autres questions! 🙂
Sandrine
C'est probablement parce qu'il y a une notion qui te cause problème. Il va falloir maîtriser cette notion puis tout ira mieux.
Posons A = ?
(3x²y + A)² = (3x²y + A)(3x²y + A) = 9x^4y² + 6Ax²y + A²
le premier terme est le même,
le troisième est tel que
A² = 16x²y^4 car c'est le terme avec les exposants les plus élevés
=> en prenant la racine carrée: A = 4xy²
et si on remplace le A dans 6Ax²y par 4xy² on trouve:
6(4xy²)x²y = 24x³y³
qui est bien le deuxième terme
conclusion A = 4xy²
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!