Secondaire 5 • 27j
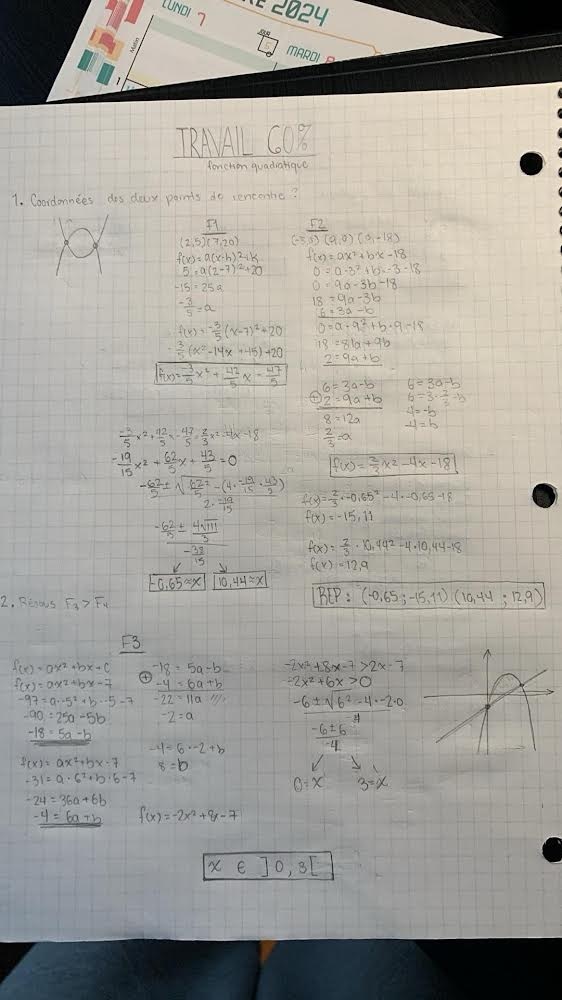
salut, voici le corrigé d’un problème de math que je n’arrive pas à comprendre. J’ai essayé de tout rendre égal à zéro les formule f1 et f2, et ensuite j’ai voulu utiliser la formule ( b+/- racine carré -b^2-4ac / 2a)pour trouver les zéros. Ça n’a pas fonctionner. Je me demande alors pourquoi. Aussi, dans le corrigé, je devrais transformer la formule en générale
mais pourquoi ?






Explication vérifiée par Alloprof
Cette explication a été vérifiée par un membre de l’équipe d’Alloprof.
Tes calculs sont bons. Mais je ne vois pas la question, as-tu bien posé le problème?
Une erreur dans le corrigé?
Note: se débarrasser des fractions facilite les calculs.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Je n'ai pas été capable de voir directement les images que tu mentionnes, mais je peux t'aider à clarifier ton problème avec la méthode que tu décris.
Voici un résumé de ce que tu sembles vouloir faire :
Étapes à suivre :
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!