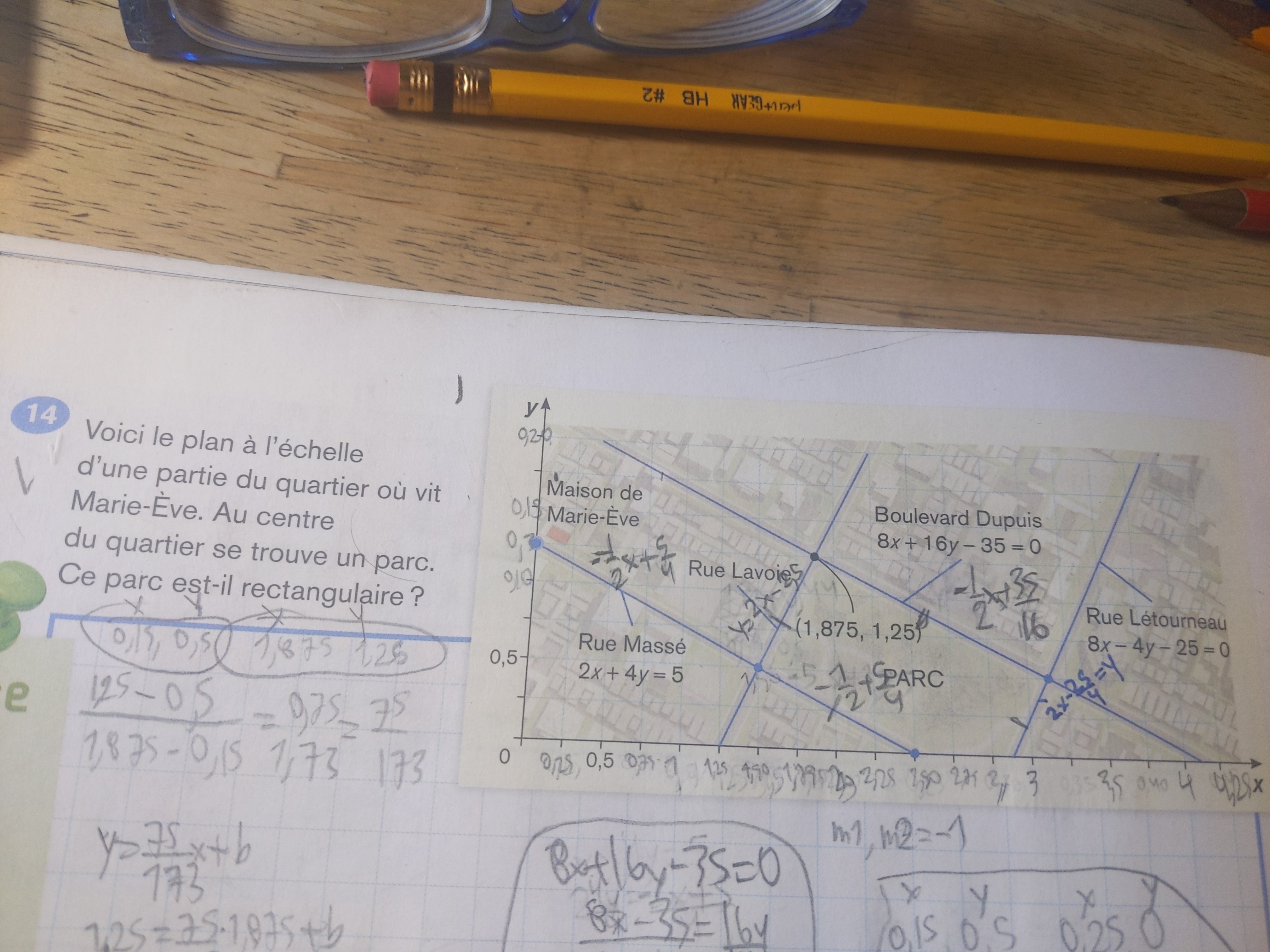
Bonjour alloprof comment je peux prouver que c'est rectangulaire. Est-ce que les deux lignes doivent avoir deux pentes la même chose et les deux autres lignes pentes la même chose merci?
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.








Tu as montré que deux rues (le boulevard Dupuis et la rue Massé) sont parallèles et une autre (la rue Létourneau) leur est perpendiculaire.
Il te reste à montrer que la rue Lavoie est parallèle à la rue Létourneau (ou encore perpendiculaire au boulevard Dupuis).
On va supposer que la rue Lavoie est bien parallèle à la rue Létourneau et tu as bien déterminé son équation en utilIsant la même pente et le poInt (1.875,1.25)
Si notre hypothèse est vraie on devrait pouvoIr établIr que les segments A, B et C sont tels que
A² + B² = C²
(trouve le poInt d'intersection des rues LavoIe et Massé et celui du boulevard Dupuis et de la rue Létourneau et calcule les distances)
s'il n'y a pas égalité, c'est que la rue Lavoie n'est pas parallèle à la rue Létourneau.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Bonjour R2D2Noble7199,
Pour répondre à ta question, tu utilises les propriétés du rectangle: deux paires de côtés parallèles isométriques. Donc, il faut trouver les mesures des côtés (pour déterminer les côtés isométriques) et calculer les pentes des segments afin de prouver qu'elles sont parallèles .
En espérant avoir répondu à ta question, bon travail
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!