Secondaire 5 • 1m
Bonjour!
J'aurais besoin d'aide pour comprendre la marche à suivre afin de trouver les 2 points d'intersections de deux fonctions racines carrés qui ce touche, je sais comment m'en sortir pour simplifier une racine carrée mais pas 2 en même temps et c'est là que je bloque.
Merci :)
exemple :
C'est un problème inventé alors les valeurs ne sont pas rondes (par exemple, sur desmos ça ma dit que un des points d'intersections c'est (-4.59808 , 3.36603))
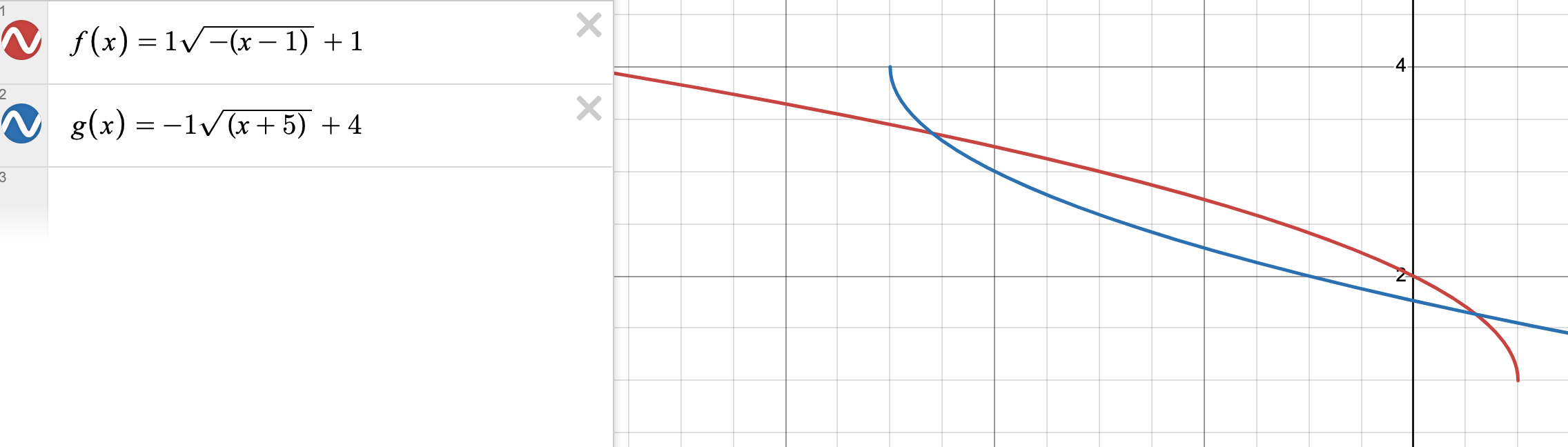






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Pour trouver le point d'intersection, nous pouvons utiliser la méthode de comparaison. Nous devrons donc résoudre cette équation :
$$1\sqrt{-(x-1)}+1=-1\sqrt{(x+5)}+4$$
On peut commencer par éliminer les facteurs 1 inutiles :
$$\sqrt{-(x-1)}+1=-\sqrt{(x+5)}+4$$
Puis, on peut déplacer une des deux constantes de l'autre côté de l'équation :
$$\sqrt{-(x-1)}+1-1=-\sqrt{(x+5)}+4-1$$
$$\sqrt{-(x-1)}=-\sqrt{(x+5)}+3$$
Ensuite, pour éliminer la racine carrée à gauche, nous allons affecter un exposant 2 aux expressions de chaque côté de l'égalité, comme ceci :
$$(\sqrt{-(x-1)})^2=(-\sqrt{(x+5)}+3)^2$$
$$-(x-1)=(-\sqrt{(x+5)}+3)^2$$
Puis, on développe l'expression au carré :
$$-(x-1)=(-\sqrt{(x+5)}+3)(-\sqrt{(x+5)}+3)$$
$$-(x-1)=-\sqrt{(x+5)}(-\sqrt{(x+5)}+3)+3(-\sqrt{(x+5)}+3)$$
On distribue la multiplication sur chaque terme :
$$-(x-1)=\sqrt{(x+5)}\sqrt{(x+5)} -3\sqrt{(x+5)} -3\sqrt{(x+5)} +9$$
$$-(x-1)=\sqrt{(x+5)}^2 -3\sqrt{(x+5)} -3\sqrt{(x+5)}+9$$
On simplifie la racine et l'exposant 2 de (x+5) :
$$-(x-1)=(x+5) -3\sqrt{(x+5)} -3\sqrt{(x+5)}+9$$
On soustrait les termes semblables :
$$-(x-1)=(x+5) -6\sqrt{(x+5)}+9$$
On additionne les constantes 5 et 9 :
$$-(x-1)=x+5 -6\sqrt{(x+5)}+9$$
$$-(x-1)=x -6\sqrt{(x+5)}+14$$
Du côté gauche de l'équation, on peut distribuer le signe dans la parenthèse :
$$-x+1=x -6\sqrt{(x+5)}+14$$
On déplace la constante 14 :
$$-x+1-14=x -6\sqrt{(x+5)}+14-14$$
$$-x-13=x -6\sqrt{(x+5)}$$
Et la variable x :
$$-x-13-x=x -6\sqrt{(x+5)}-x$$
$$-2x-13= -6\sqrt{(x+5)}$$
On élimine le coefficient -6 :
$$\frac{-2x}{-6}+\frac{-13}{-6}= \frac{-6\sqrt{(x+5)}}{-6}$$
$$\frac{x}{3}+\frac{13}{6}= \sqrt{(x+5)}$$
Maintenant, on doit de nouveau affecter un exposant 2 de chaque côté, afin d'éliminer la racine carrée à droite :
$$(\frac{x}{3}+\frac{13}{6})^2= (\sqrt{(x+5)})^2$$
$$(\frac{x}{3}+\frac{13}{6})^2= x+5$$
On doit ensuite développer l'expression à gauche, comme on a fait précédemment. Tu devras ensuite résoudre l'équation de second degré. Consulte cette fiche au besoin : Résoudre une équation ou une inéquation de degré 2 | Secondaire | Alloprof
Je te laisse terminer le calcul. J'espère que cela t'aide! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!