Zone d’entraide

FauconEfficace7471

Bonjour!

J'aurais besoin d'aide pour comprendre la marche à suivre afin de trouver les 2 points d'intersections de deux fonctions racines carrés qui ce touche, je sais comment m'en sortir pour simplifier une racine carrée mais pas 2 en même temps et c'est là que je bloque.

Merci :)

exemple :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

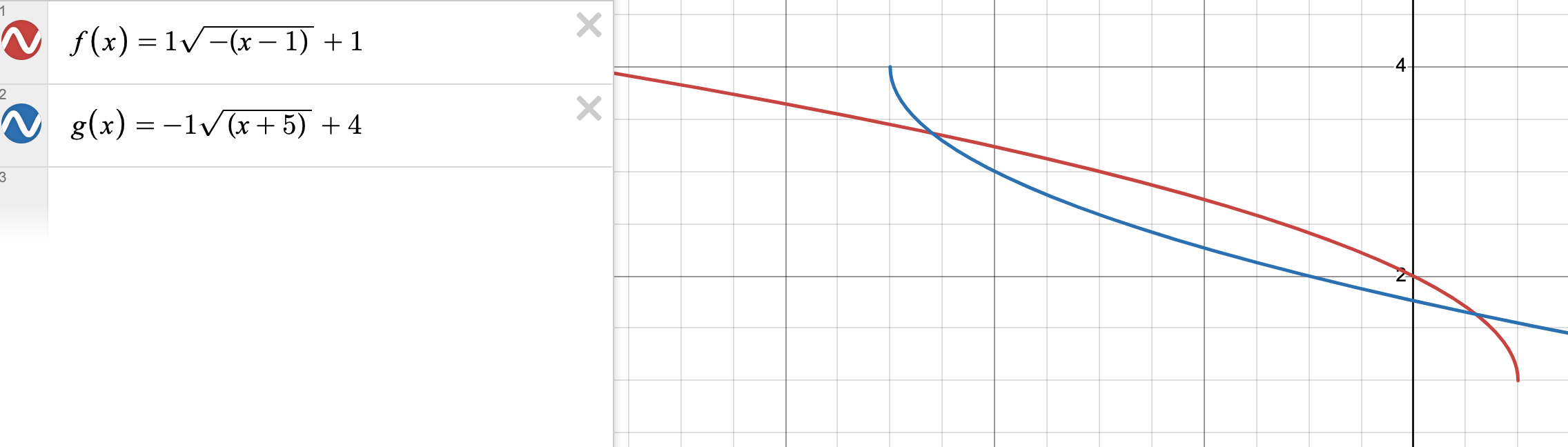
C'est un problème inventé alors les valeurs ne sont pas rondes (par exemple, sur desmos ça ma dit que un des points d'intersections c'est (-4.59808 , 3.36603))

Katia K

Salut!

Pour trouver le point d'intersection, nous pouvons utiliser la méthode de comparaison. Nous devrons donc résoudre cette équation :

$$1\sqrt{-(x-1)}+1=-1\sqrt{(x+5)}+4$$

On peut commencer par éliminer les facteurs 1 inutiles :

$$\sqrt{-(x-1)}+1=-\sqrt{(x+5)}+4$$

Puis, on peut déplacer une des deux constantes de l'autre côté de l'équation :

$$\sqrt{-(x-1)}+1-1=-\sqrt{(x+5)}+4-1$$

$$\sqrt{-(x-1)}=-\sqrt{(x+5)}+3$$

Ensuite, pour éliminer la racine carrée à gauche, nous allons affecter un exposant 2 aux expressions de chaque côté de l'égalité, comme ceci :

$$(\sqrt{-(x-1)}{)}^2=(-\sqrt{(x+5)}+3{)}^2$$

$$-(x-1)=(-\sqrt{(x+5)}+3{)}^2$$

Puis, on développe l'expression au carré :

$$-(x-1)=(-\sqrt{(x+5)}+3)(-\sqrt{(x+5)}+3)$$

$$-(x-1)=-\sqrt{(x+5)}(-\sqrt{(x+5)}+3)+3(-\sqrt{(x+5)}+3)$$

On distribue la multiplication sur chaque terme :

$$-(x-1)=\sqrt{(x+5)}\sqrt{(x+5)}-3\sqrt{(x+5)}-3\sqrt{(x+5)}+9$$

$$-(x-1)={\sqrt{(x+5)}}^2-3\sqrt{(x+5)}-3\sqrt{(x+5)}+9$$

On simplifie la racine et l'exposant 2 de (x+5) :

$$-(x-1)=(x+5)-3\sqrt{(x+5)}-3\sqrt{(x+5)}+9$$

On soustrait les termes semblables :

$$-(x-1)=(x+5)-6\sqrt{(x+5)}+9$$

On additionne les constantes 5 et 9 :

$$-(x-1)=x+5-6\sqrt{(x+5)}+9$$

$$-(x-1)=x-6\sqrt{(x+5)}+14$$

Du côté gauche de l'équation, on peut distribuer le signe dans la parenthèse :

$$-x+1=x-6\sqrt{(x+5)}+14$$

On déplace la constante 14 :

$$-x+1-14=x-6\sqrt{(x+5)}+14-14$$

$$-x-13=x-6\sqrt{(x+5)}$$

Et la variable x :

$$-x-13-x=x-6\sqrt{(x+5)}-x$$

$$-2x-13=-6\sqrt{(x+5)}$$

On élimine le coefficient -6 :

$$\frac{-2x}{-6}+\frac{-13}{-6}=\frac{-6\sqrt{(x+5)}}{-6}$$

$$\frac{x}{3}+\frac{13}{6}=\sqrt{(x+5)}$$

Maintenant, on doit de nouveau affecter un exposant 2 de chaque côté, afin d'éliminer la racine carrée à droite :

$$(\frac{x}{3}+\frac{13}{6}{)}^2=(\sqrt{(x+5)}{)}^2$$

$$(\frac{x}{3}+\frac{13}{6}{)}^2=x+5$$

On doit ensuite développer l'expression à gauche, comme on a fait précédemment. Tu devras ensuite résoudre l'équation de second degré. Consulte cette fiche au besoin : Résoudre une équation ou une inéquation de degré 2 | Secondaire | Alloprof

Je te laisse terminer le calcul. J'espère que cela t'aide! :)