Secondaire 4 • 1m
1)Bonjour alloprof je ne sais pas comment je peux faire ça en effet je n'ai pas bien compris ces deux problèmes?
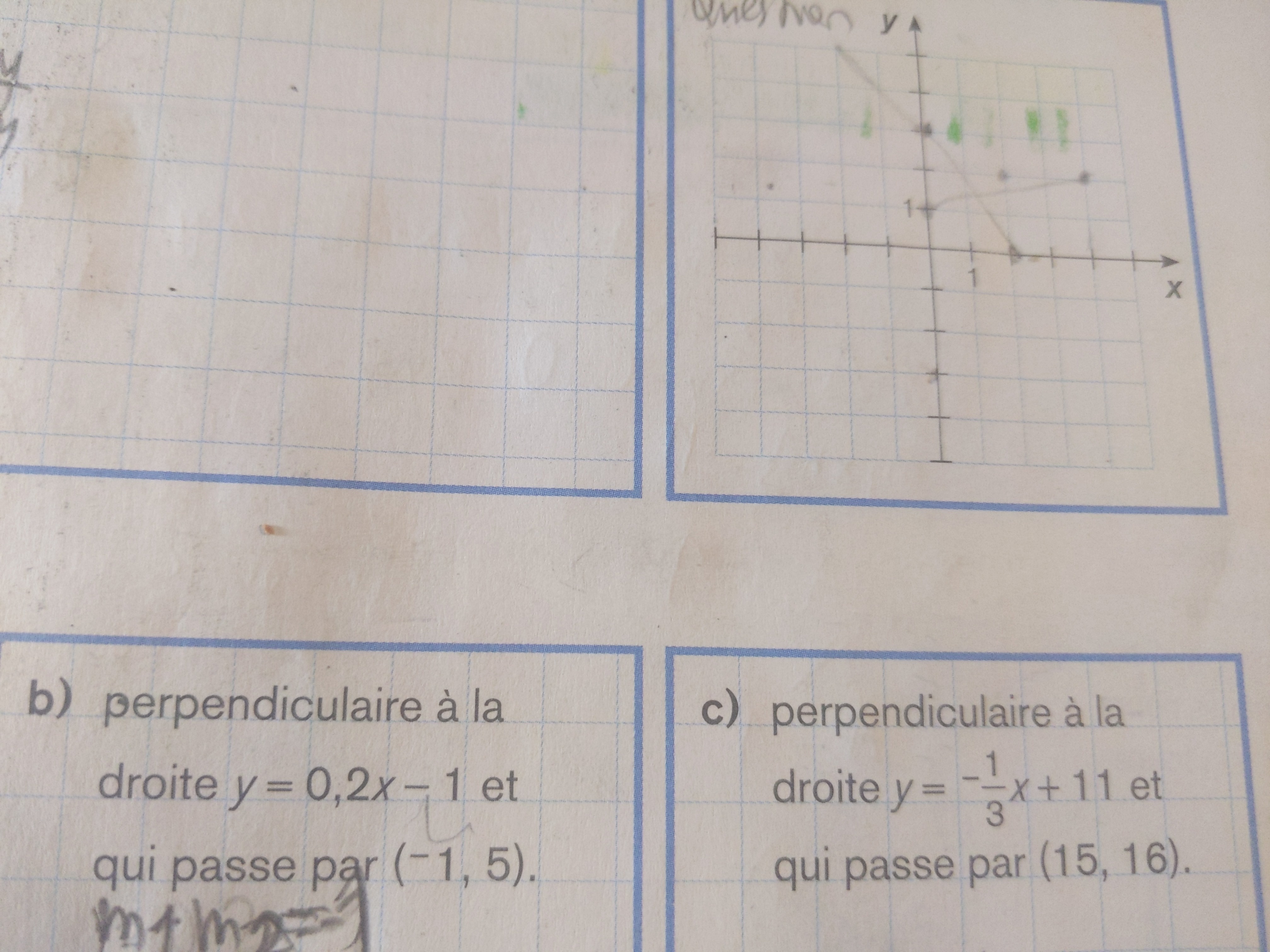
1)Dans le numéro 11 est-ce que je dois faire m1xm2=-1 pour perpendiculaire ?
2)Expliquez la consigne s'il vous plaît parce que ce n'est pas à cause du perpendiculaire m1xm2=-1 ?
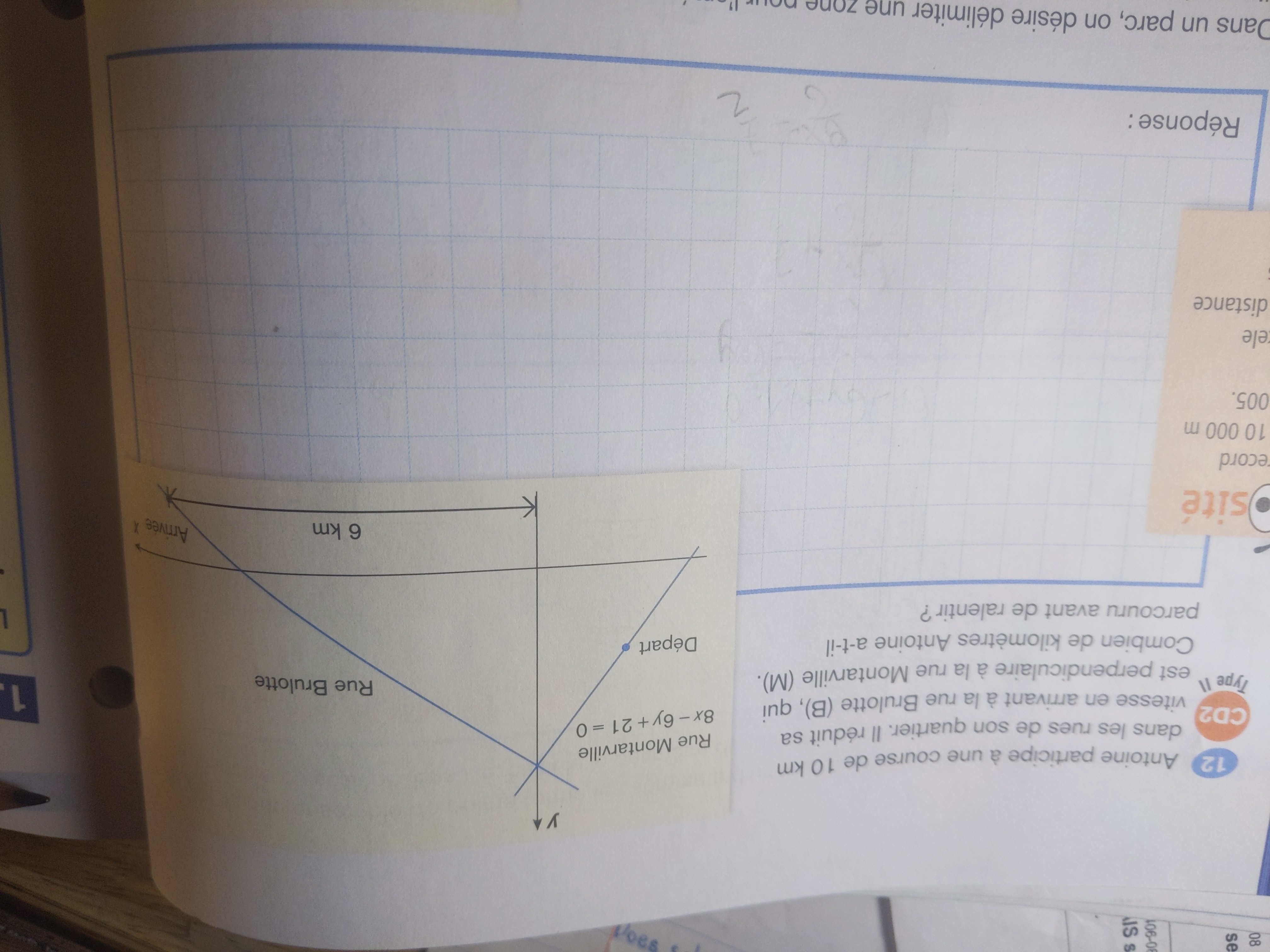
3) bonjour il y a la rue Montarville est-ce que je dois trouver l'équation de le
droite
4) pour la rue de Brulotte je ne sais pas comment je peux trouver l'équation
À partir de maintenant je vous répète lisez bien s'il vous plaît et répondez bien à ma question. Merci pour votre compréhension








Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut !
Tous les exercices ont pour thème les droites parallèles et perpendiculaires. Donc tout d'abord, voici une fiche explicative sur le sujet que tu peux relire au besoin pour te remettre à jour sur la matière et comment trouver les valeurs de pentes.
Dans la première image, comme la droite que tu cherche est perpendiculaire à celle dont on te donner la règle, tu peux trouver la pente :
$$ m_1 \times m_2 = -1 $$
Et ensuite la règle \(y=mx+b\) avec le point de coordonnées qu'on te donne.
Pour la deuxième image, tu dois trouver la pente des droites diagonales (rouge et orange).
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Comme tu as deux points de ces droites, tu peux trouver le taux de variation (la pente) comme suit :
$$ a=\frac{y_2-y_1}{x_2-x_1} $$
Puis, tu dois aussi trouver la mesure de ces diagonales en trouver les distances AC et BD.
$$ \text{dist}(A,B)=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} $$
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour la troisième image, tu peux trouver la règle de la fonction qui représente la rue Brulotte, car elle est perpendiculaire à la fonction de la rue Montarville est de forme \(Ax+By+C=0\).
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Pour pouvoir répondre aux autres usagers, je t'invite à commencer les exercices par toi-même avec les explications données et si tu as d'autres questions, n'hésite pas !
Bonne soirée !
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!