Bonjour allo prof
J'ai quelques question, pouvez-vous m'aider svp???
Dans l'exercice du cahier il y a avait cela, mais je ne suis sure que ce soit bon que le moins soit devant une valeur absolue si elle était dedans avant
Une autre question est est-ce que si on fait une graphic et les graduation de l'axe des x et y n'est pas la même graduation, est-ce que ses grave?
Une autre question est si j'ai x = 3y +1 ça donne -3y = -x+1 et donc je peut multiplier par -3 partout et ça me donne y = -x+1/-3 ou est-ce que je peux dire y = x/3 - 1/3
Une autre de mes question est: lorsque je veut faire la résolution d'une valeur absolue donc la fonction valeur absolue = à quelque chose (constante ou droite) lorsque je doit mettre ma valeur absolue positivé et négative ce qui va me donner 2 équation, est-ce que quand je fait ça je crée les 2 demi-droite = à la droite ou la constante que la fonction du départ était égale??
une autre question est si lors d'une résolution de valeur absolue je tombe avec une valeur absolue = à un négatif, qu'est-ce que devrais écrire dans ma réponse??
Une autre de mes questions est si je fait le dessin d'une fonction valeur absolue est-ce que je le fait avec le b ou pas de b??
Une autre mes question est si je dois faire l'analyse d'une fonction et qu'il ya une constante, est-ce que je dois L'inclure quand je fait l'intervalle pour la croissante??
Une autre chose que je ne comprend pas est pourquoi lorsqu'on fait la racine cubique on peut aussi dire à la 1/3?
une autre question est si j'ai une fonction valeur absolue sous cette forme est-ce que ses pareil bon?
Je n'arrive pas a comprendre cette question, je croyais que le a servais de taux de variation, mais il n'y pas de ce choix dedans les choix de réponse
Je ne comprend pas à quoi set le moins
Désolé, j'avais beaucoup de question, j'aurais voulu poser mes questions au prof, mais il est arriver un imprévu, alors merci à l'avance !!!!
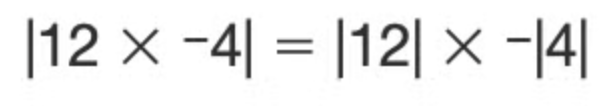
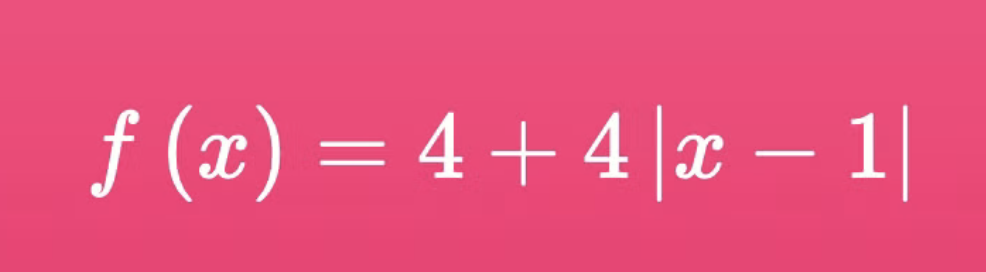







Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Merci de nous avoir contactés! :)
Concernant ta première équation, tu as bien raison, ceci est faux :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le résultat de |12×-4| est |-48|=48, tandis que le résultat de |12| × -|4| est 12 × -4 = -48. L'équation n'est donc pas vraie.
On peut distribuer la valeur absolue sur la multiplication :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Mais on ne peut pas déplacer le signe négatif en dehors de la valeur absolue!
Je pense qu'il s'agit d'une erreur dans ton cahier, tu peux en faire part à ton professeur pour qu'il puisse la rectifier :)
Pour ta deuxième question, il n'est pas obligatoire d'avoir les mêmes graduations pour l'axe des x et l'axe des y. Voici un exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ensuite, si tu veux isoler y dans l'équation x = 3y +1, tu auras ceci :
$$x = 3y +1 $$
$$-3y = -x+1 $$
Il ne faut pas multiplier par -3, mais plutôt diviser par -3.
$$\frac{-3y}{-3} = \frac{-x}{-3}+\frac{1}{-3} $$
$$y = \frac{x}{3}-\frac{1}{3} $$
Ce qui est équivalent à y = -x+1/-3. Tu peux choisir la forme que tu veux, mais j'opterais pour l'équation y = x/3 - 1/3 si j'étais toi, puisque les paramètres \(a\) et \(b\) sont plus faciles à identifier.
Concernant la question suivante, je ne suis pas sûre de l'avoir bien comprise. Pour résoudre une équation contenant une valeur absolue, tu dois commencer par isoler cette valeur absolue. Puis, tu obtiendras deux équations, l'une avec l'expression dans la valeur absolue, et l'autre avec la même expression dans la valeur absolue, mais avec un signe négatif devant. Tu ne dois pas toucher à l'autre côté de l'égalité (celui qui ne contient pas la valeur absolue) à cette étape-ci. Voici un exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Je te conseille de jeter un coup d'oeil à cette fiche, tu y trouveras plusieurs exemples similaires : Résoudre une équation ou une inéquation contenant une valeur absolue | Secondaire | Alloprof
Si dans ta résolution tu as une valeur absolue égale à un nombre négatif, tu dois arrêter le calcul! En effet, puisqu'une valeur absolue ne peut pas être égale à un nombre négatif, cela signifie qu'il n'y a pas de solution tout simplement! Voici un exemple :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ensuite, pour tracer le graphique d'une fonction valeur absolue, tu dois utiliser la forme sans le paramètre b, soit :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Si tu as un paramètre b, tu peux le sortir de la valeur absolue avec cette propriété :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Puis multiplier le résultat par le paramètre a pour fusionner les deux paramètres.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici une fiche qui pourrait t'être utile : Tracer une fonction valeur absolue | Secondaire | Alloprof
Concernant ta question sur l'analyse de fonction, je pense que la constante dont tu fais référence est le paramètre k. Le paramètre k a pour effet de faire glisser une fonction vers le bas ou vers le haut, tout dépendant de sa valeur. La constante n'affecte pas si la fonction est croissante ou décroissante, car elle ne change pas la pente de la fonction (elle déplace simplement la droite vers le haut ou le bas). Par exemple, si tu as la fonction f(x) = 2x + 5, la constante 5 n'affecte pas l'intervalle de croissance. Ce qui importe ici, c'est la pente 2, qui est positive, donc la fonction est croissante sur tout son domaine. Voici une fiche pour en apprendre plus sur l'effet des différents paramètres : Le rôle des paramètres a, b, h et k d’une fonction en forme canonique | Secondaire | Alloprof
Puis, on dit que la racine cubique d'un nombre est égale à ce nombre affecté d'un exposant 1/3 à cause de cette loi des exposants :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voici des exemples :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ensuite, cette forme est bien la forme canonique :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On a simplement mis le paramètre k en premier, mais l'ordre des termes ne change rien!
$$ f(x)=4+4|x-1|=4|x-1|+4$$
De plus, il n'y a pas de pente dans la fonction valeur absolue (tu confonds avec la fonction affine). Chaque branche de la fonction valeur absolue a sa propre pente. Le paramètre \(a\) a l'effet suivant :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu trouveras la réponse à cette question :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Dans cette fiche :
Ou celle-ci, qui est plus générale (l'effet des paramètres pour toutes les fonctions) :
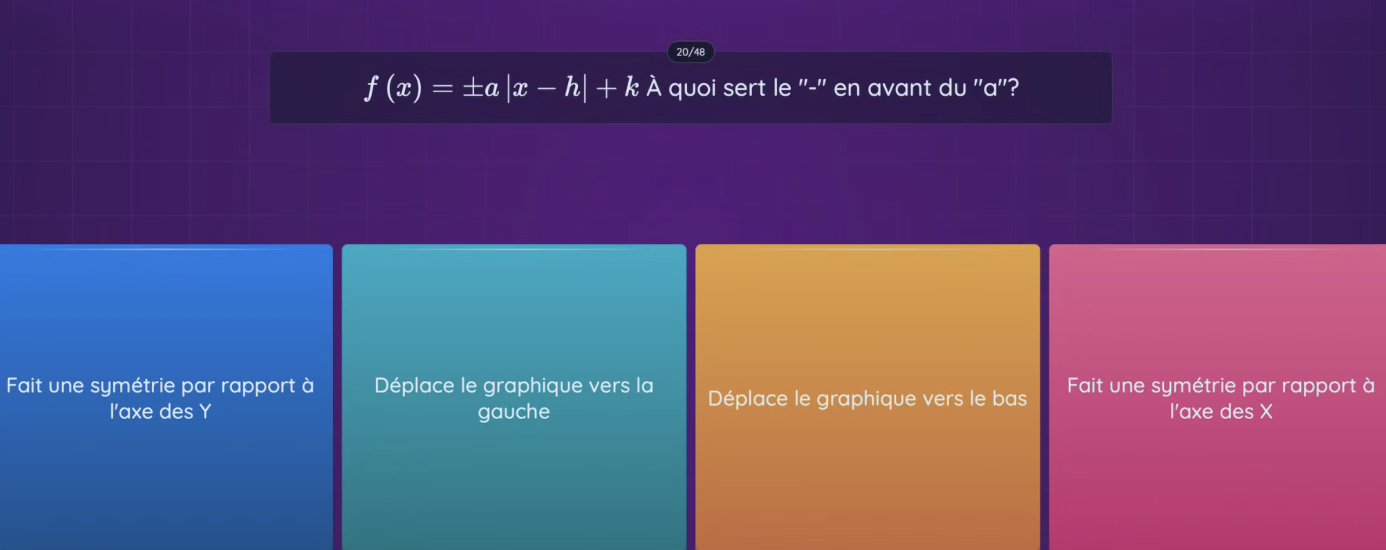
Tu y trouveras également la réponse à cette question :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le signe négatif a l'effet suivant sur la fonction :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Voilà! J'espère que cela répond à toutes tes questions! :) Je te suggère cependant la prochaine fois de séparer tes questions en plusieurs petites publications, cela nous permettrait de te donner des réponses plus rapidement, puisque nous pourrions nous répartir les questions et y répondre au fur et à mesure :)
J'espère que le tout est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!