Secondaire 5 • 2m
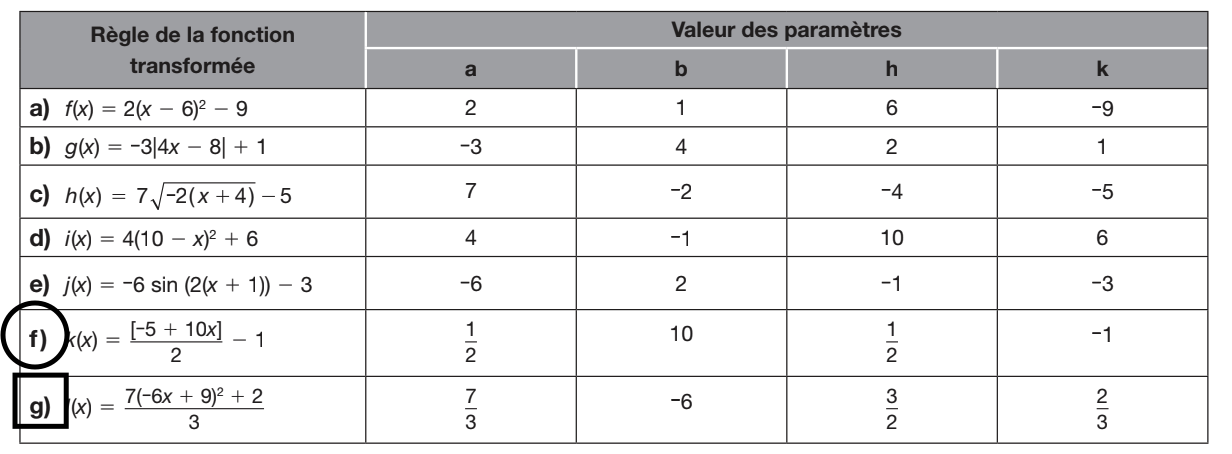
Bonjour, il y a un numéro que je n'arrive vraiment pas à comprendre, je ne comprend pas pourquoi le numéro f), car la valeur du paramètre b m'a donner 5 et le corriger donne 10 et au numéro g), la valeur de mon b est de -2 et le corriger donne -6, pouvez-vous m'expliquer svp??
Merci à l'avance






Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Pour le numéro f),
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Que l'on peut réécrire comme ceci :
$$ k(x) = \frac{1}{2} [10x-5] -1$$
On doit factoriser 10 dans les crochets, car le coefficient de la variable x doit être de 1 pour avoir la forme canonique de l'équation :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Ce qui nous donne :
$$ k(x) = \frac{1}{2} [10(x-\frac{5}{10})] -1$$
$$ k(x) = \frac{1}{2} [10(x-\frac{1}{2})] -1$$
Donc, le paramètre b est de 10, et le paramètre h est de 1/2.
Si tu factorises seulement 5 comme on ferait en temps normal pour une simple factorisation d'expression, tu obtiendrais alors ceci :
$$ k(x) = \frac{1}{2} [5(2x-1)] -1$$
Ce qui n'est pas la forme canonique de l'équation, car le coefficient de la variable x est de 2, et ce 2 ne représente pas un paramètre. Il est important que chaque nombre présent dans l'équation soit un paramètre connu (a, b, h ou k).
Concernant le numéro g),
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Que l'on peut réécrire comme ceci :
$$ l(x) = \frac{7}{3} (-6x+9)^2 + \frac{2}{3}$$
On a la même situation que le numéro précédent, on ne doit pas avoir de coefficient devant notre variable x. Donc, nous devons éliminer le -6 en le factorisant, comme ceci :
$$ l(x) = \frac{7}{3} (-6(x+\frac{9}{-6}))^2 + \frac{2}{3}$$
$$ l(x) = \frac{7}{3} (-6(x-\frac{3}{2}))^2 + \frac{2}{3}$$
Voilà! J'espère que c'est plus clair pour toi! :)
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!