
Les composantes d'un vecteur
Secondaire 5
Lorsqu’on place un vecteur dans un plan cartésien, on peut le caractériser selon les déplacements à l’horizontale (en x) et à la verticale (en y) entre son origine et son extrémité. Ces déplacements, que l’on nomme composantes, nous permettent de calculer la norme du vecteur ainsi que son orientation. Inversement, on peut trouver les composantes d’un vecteur à l’aide de sa norme et de son orientation.
Les composantes d’un vecteur
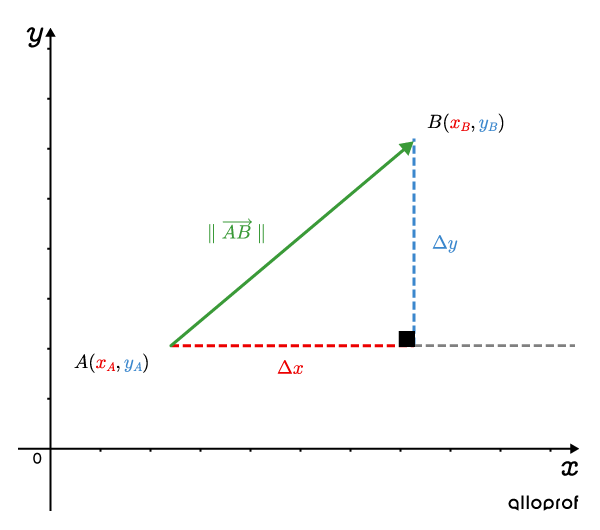
Lorsqu'un vecteur est représenté dans un plan cartésien, on peut former un triangle rectangle dans lequel l’hypoténuse correspond au vecteur et les cathètes correspondent à ses composantes en x et en y.
Soit 2 points du plan cartésien, A(xA,yA) et B(xB,yB). On définit le vecteur →AB de la façon suivante :→AB=(Δx,Δy)=(xB−xA,yB−yA)=(a,b)
L’animation interactive suivante permet de mieux visualiser le rôle des composantes d’un vecteur en tant que cathètes d’un triangle rectangle.
Quelles sont les composantes a et b du vecteur →AB suivant?
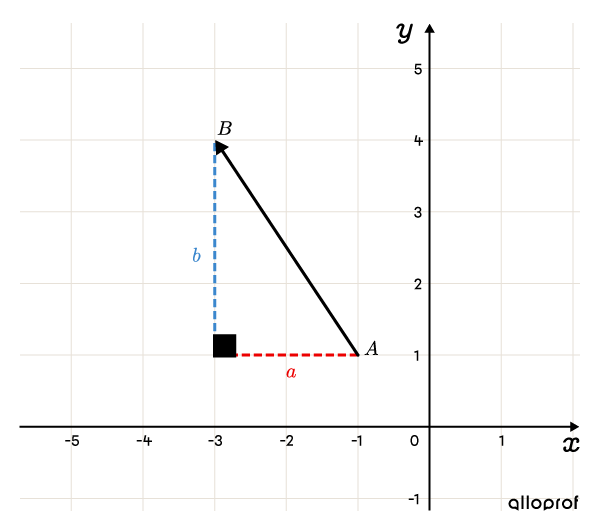
Les coordonnées du point A, qui correspond à l’origine du vecteur, sont (−1,1). Quant au point B, qui correspond à l’extrémité du vecteur, ses coordonnées sont (−3,4). Pour calculer la composante horizontale a, on a :a=Δx=xB−xA=−3−−1=−2Pour ce qui est de la composante verticale b, on a :b=Δy=yB−yA=4−1=3Ainsi, les composantes du vecteur →AB sont (−2,3).
Important!
Soit →RS et →TU, 2 vecteurs opposés qui ont la même norme et la même direction, mais qui sont de sens contraire.
Si les composantes de →RS sont (a,b), alors les composantes de →TU sont nécessairement (−a,−b).
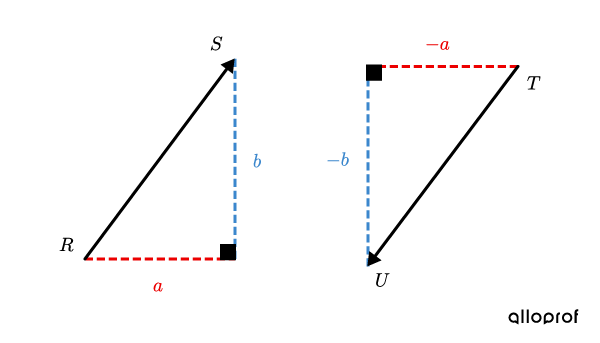
Les relations trigonométriques dans un vecteur
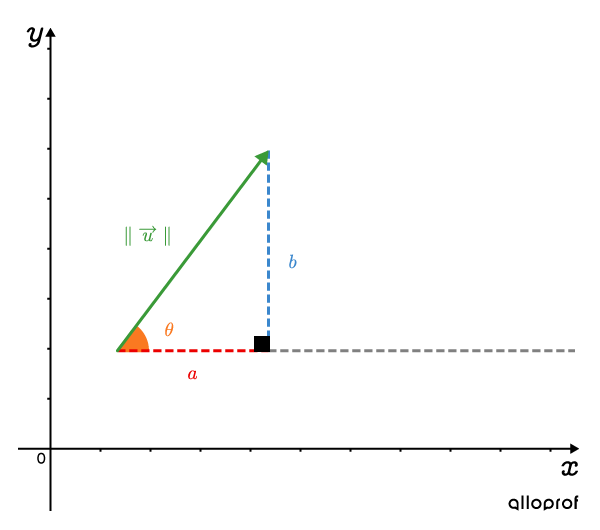
Soit un vecteur →u quelconque. À l’aide des rapports trigonométriques dans un triangle rectangle, on peut déterminer des relations entre les composantes a et b, la norme ∥→u∥ et l’orientation θ de ce vecteur.cosθ=a∥→u∥sinθ=b∥→u∥tanθ=ba
Attention!
Ces relations trigonométriques sont valides seulement si l’angle θ est défini par rapport à un axe horizontal.
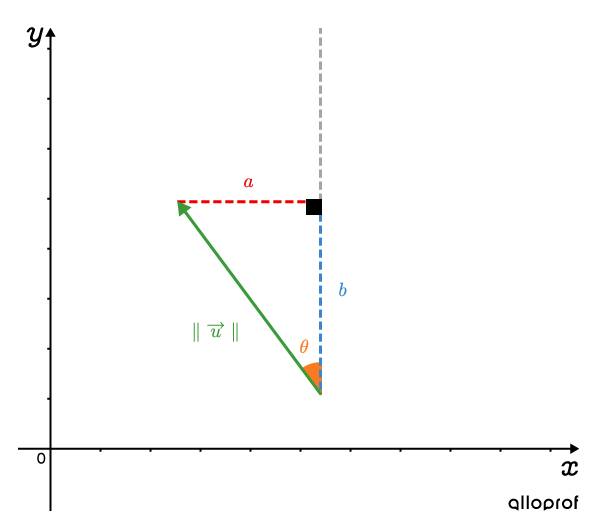
Pour un vecteur →u dont l’angle θ est défini par rapport à un axe vertical comme dans cette image, on obtient plutôt les relations trigonométriques suivantes.cosθ=b∥→u∥sinθ=a∥→u∥tanθ=ab
Le calcul des composantes d’un vecteur
Lorsqu’on cherche à calculer les composantes d’un vecteur, on se retrouve inévitablement devant l’une des situations suivantes.
La norme et une composante du vecteur sont connues
Lorsqu’on connait la norme et une composante d’un vecteur, il est possible de calculer l’autre composante à l’aide de la relation de Pythagore.
Quelle est la composante verticale b du vecteur →u dont la composante horizontale est a=−8,4 et la norme est ∥→u∥=14?
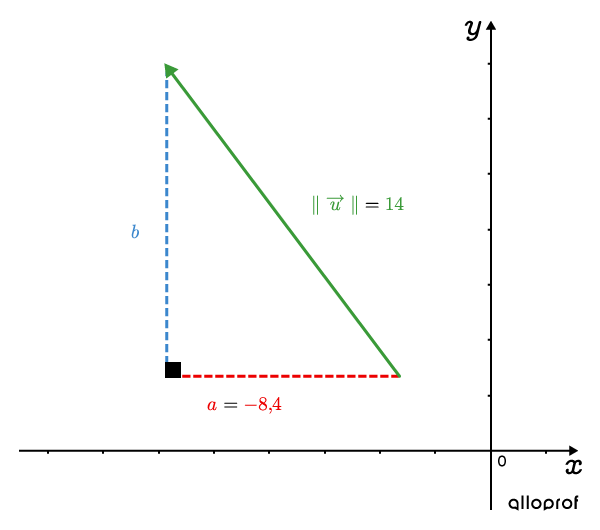
À partir du triangle rectangle formé par le vecteur →u, on peut utiliser la relation de Pythagore.
a2+b2=∥→u∥2(−8,4)2+b2=14270,56+b2=196b2=125,44b=±11,2
On rejette −11,2, car le déplacement vertical du vecteur →u se fait dans le sens positif de l’axe des y. Ainsi, la composante verticale du vecteur →u est b=11,2.
L’orientation et une composante du vecteur sont connues
Lorsqu’on connait l’orientation et une composante d’un vecteur, il est possible de calculer l’autre composante à l’aide du rapport tangente.
Soit un vecteur →u=(a,b) dont l’orientation θ et l’une des composantes sont connues. À partir des relations trigonométriques dans un vecteur, on a :tanθ=baEn isolant a et b respectivement, on obtient les formules suivantes.a=btanθb=atanθ
Quelle est la composante horizontale a du vecteur →u dont la composante verticale est b=4,45 et l’orientation est θ=51∘?
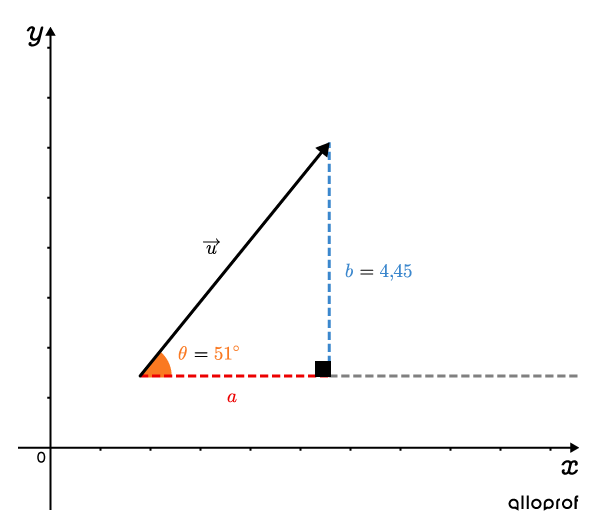
À partir du triangle rectangle formé par le vecteur →u, on peut utiliser la formule pour calculer la composante horizontale a.a=btanθ=4,45tan51∘a≈3,6Ainsi, la composante horizontale du vecteur →u est 3,6.
L’orientation et la norme du vecteur sont connues
Lorsqu’on connait l’orientation et la norme d’un vecteur, il est possible de calculer les composantes à l’aide des rapports trigonométriques.
Soit un vecteur →u=(a,b) dont la norme ∥→u∥ et l’orientation θ sont connues. À partir des relations trigonométriques dans un vecteur, on a :cosθ=a∥→u∥sinθ=b∥→u∥En isolant a et b respectivement, on obtient les formules suivantes.a=∥→u∥cosθb=∥→u∥sinθ
Quelles sont les composantes du vecteur →u dont la norme est ∥→u∥=5,8 et l’orientation est θ=320∘?
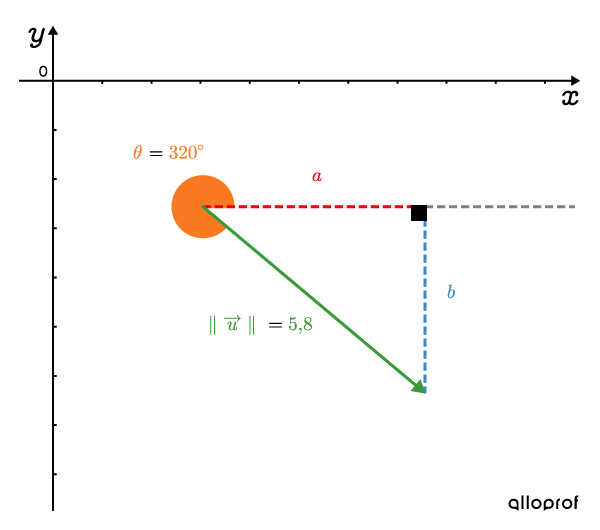
À partir du triangle rectangle formé par le vecteur →u, on peut utiliser la formule pour calculer la composante horizontale a. a=∥→u∥cosθa=5,8cos320∘a≈4,44Quant à la composante verticale b, on a :b=∥→u∥sinθb=5,8sin320∘b≈−3,73Ainsi, les composantes du vecteur →u sont (4,44;−3,73).
Le calcul de la norme d’un vecteur à partir de ses composantes
Un vecteur peut être représenté par un triangle rectangle et on peut calculer sa norme à partir de ses composantes en utilisant la relation de Pythagore.
Quelle est la norme du vecteur →u dont la composante horizontale est a=−5,6 et la composante verticale est b=−4,2?
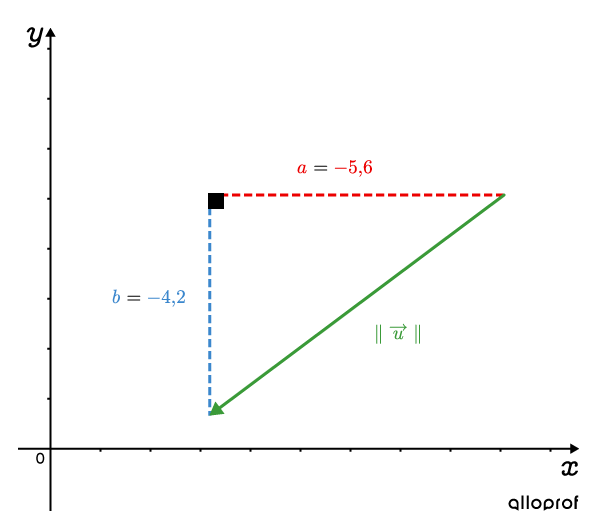
En appliquant directement la relation de Pythagore, on a :∥→u∥2=a2+b2=(−5,6)2+(−4,2)2=49∥→u∥=±√49=±7On rejette −7 comme valeur puisque la norme d’un vecteur est toujours positive. Ainsi, la norme du vecteur →u est ∥→u∥=7.
Important!
Si on connait les coordonnées de l’origine A(xA,yA) et de l’extrémité B(xB,yB) d'un vecteur →AB, on calcule plutôt la norme en utilisant la formule de la distance entre deux points.∥→AB∥=√Δx2+Δy2=√(xB−xA)2+(yB−yA)2
Le calcul de l’orientation d’un vecteur à partir de ses composantes
Lorsqu’on connait les composantes (a,b) d'un vecteur →u, il est possible de déterminer son orientation θ à l’aide des rapports trigonométriques.
Important!
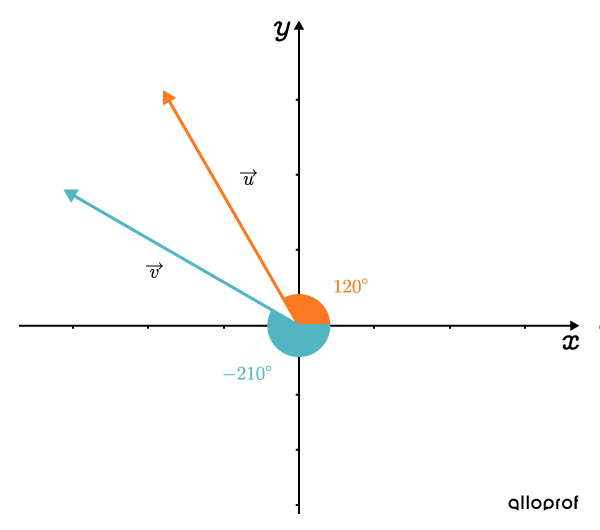
Par convention, l'orientation d’un vecteur est donnée par l'angle qu’il forme avec l'axe des x positifs dans le sens antihoraire. Le vecteur →u dans l’image en est un exemple.
Toutefois, il est possible qu’un angle ait une valeur négative, comme le vecteur →v de la même image. Ceci signifie que l’orientation de ce vecteur est l’angle qu’il forme avec l’axe des x positifs dans le sens horaire.
Soit un vecteur →u dont les composantes a et b sont connues. Afin de calculer l’orientation θ de ce vecteur, il est nécessaire d’utiliser la réciproque de la fonction tangente.
Toutefois, la fonction arctan ne donne que des valeurs d’angle entre −90∘ et 90∘. C’est la raison pour laquelle on utilise θ ′ pour représenter le résultat de la fonction arctan et θ pour représenter l’orientation du vecteur →u. Ainsi, à partir des relations trigonométriques dans un vecteur, on a :tanθ ′=baEn isolant θ ′, on obtient la formule suivante.θ ′=arctan(ba)
Il est préférable de faire une esquisse du vecteur selon le signe des composantes a et b. À l’aide de cette esquisse et du tableau ci-dessous, on applique la correction nécessaire à l’angle θ ′ afin d’obtenir l’orientation θ du vecteur →u dont la mesure est entre 0∘ et 360∘.
| a>0 | a<0 | |
|---|---|---|
| b>0 |
θ=θ ′+0∘  |
θ=θ ′+180∘  |
| b<0 |
θ=θ ′+360∘ 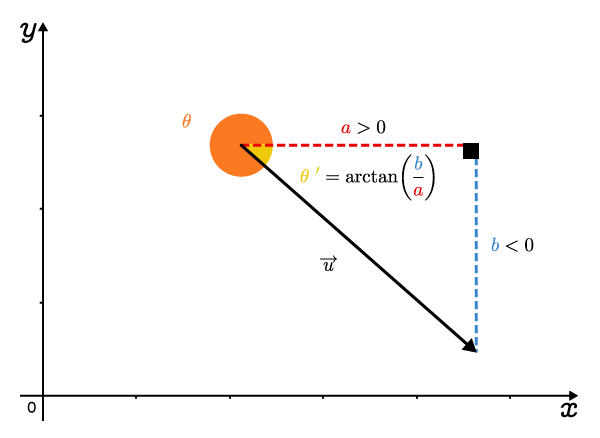 |
θ=θ ′+180∘  |
Pour déterminer l’orientation θ d’un vecteur à partir de ses composantes, on peut suivre les étapes suivantes.
Règle
-
Déterminer les composantes a et b du vecteur.
-
Calculer l’orientation θ ′ du vecteur à l’aide de la formule θ ′=arctan(ba).
-
Analyser le signe des composantes a et b et appliquer la correction à la valeur de θ ′, au besoin.
-
Donner l’orientation θ du vecteur.
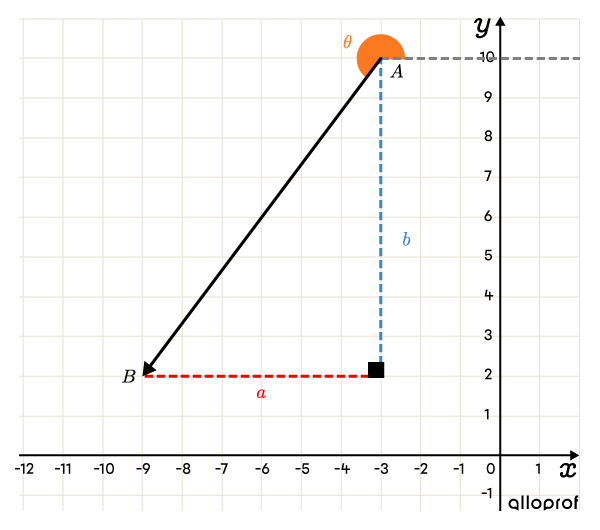
Quelle est l’orientation du vecteur →AB suivant?
-
Déterminer les composantes a et b du vecteur
Les coordonnées du point A sont (−3,10) et celles du point B sont (−9,2). On a alors :→AB=(a,b)=(xB−xA,yB−yA)=(−9−−3,2−10)=(−6,−8) -
Calculer l’orientation θ ′ du vecteur
θ ′=arctan(ba)=arctan(−8−6)θ ′≈53,13∘ -
Analyser le signe des composantes a et b et appliquer la correction à la valeur de θ ′
Puisque a<0 et b<0, on doit ajouter 180∘ à θ ′ pour obtenir l’orientation θ. On a :θ=θ ′+180∘=53,13∘+180∘=233,13∘ -
Donner l’orientation θ du vecteur
Ainsi, l'orientation θ du vecteur →AB=(−6,−8) est de 233,13∘.
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :

À voir aussi
- Les vecteurs
- La comparaison entre deux vecteurs
- L'addition et la soustraction de vecteurs
- La multiplication de vecteurs par un scalaire et le produit scalaire
- La combinaison linéaire de vecteurs
- Les propriétés des opérations sur les vecteurs
- La projection orthogonale d'un vecteur
- La démonstration des propositions portant sur les vecteurs
- La résolution de problèmes impliquant les vecteurs
Dans cette page
- Haut de page
- Les composantes d’un vecteur
- Les relations trigonométriques dans un vecteur
- Le calcul des composantes d’un vecteur
- La norme et une composante du vecteur sont connues
- L’orientation et une composante du vecteur sont connues
- L’orientation et la norme du vecteur sont connues
- Le calcul de la norme d’un vecteur à partir de ses composantes
- Le calcul de l’orientation d’un vecteur à partir de ses composantes
- À voir aussi















































