Trouver la règle d'une fonction logarithmique

Les valeurs de |\boldsymbol{b}| et |\boldsymbol{c}| sont connues

Trouvez l'équation de la fonction logarithmique passant par le point (5, -3) dont la valeur du paramètre |b| vaut 2 et celle de la base |c| vaut 10.

On remplace |\color{blue}{b}|, |\color{red}{c}|, |\color{green}{x}| et |\color{purple}{y}| dans l'équation.
||\begin{align}\color{purple}{y} &= a \log_{\color{red}{c}} \big(\color{blue}{b}(\color{green}{x})\big)\\ \color{purple}{-3} &= a \log_{\color{red}{10}} \big(\color{blue}{2} \times \color{green}{5}\big)\\-3 &= a \end{align}||
Réponse : l'équation est |y=-3 \log \big(2(x)\big).|

Les valeurs de |\boldsymbol{a}| et |\boldsymbol{c}| sont connues

Trouvez l'équation de la fonction logarithmique passant par le point (-12, 8) dont la valeur de la base |c| vaut 2 et celle du paramètre |a| vaut -4.

On remplace |\color{magenta}{a}|, |\color{red}{c}|, |\color{green}{x}| et |\color{purple}{y}| dans l'équation.
||\begin{align}\color{purple}{y} &= \color{magenta}{a}\log_{\color{red}{c}} \big(b(\color{green}{x})\big)\\ \color{purple}{8} &= \color{magenta}{-4} \log_{\color{red}{2}} \big(b \times \color{green}{-12}\big) \end{align}||
On isole l'expression contenant le logarithme.
||-2 = \log_2 (-12b)||
On passe à la forme exponentielle afin d'isoler le |b|.
||\begin{align}2^{-2} &= -12b\\ \dfrac{2^{-2}}{-12} &= b\\ \dfrac{\text{-}1}{48}&=b \end{align}||
Réponse : l'équation est |y= -4 \log_2 \left(\dfrac{\text{-}1}{48}(x) \right).|

La valeur de |\boldsymbol{a}| est connue

Trouvez l'équation d'une fonction logarithmique dont la valeur du paramètre |a| vaut |4| et qui passe par les points |(0{,}25; -4)| et |(128, 8).|

En remplaçant |a| par |4,| on a l'équation |y= 4 \log_c \big(b(x)\big).|

On remplace |x| et |y| par les coordonnées dans l'équation.

On obtient alors |-4 = 4 \log_c (b \times 0{,}25)| et |8 = 4 \log_c (b \times 128).|

Il faut maintenant isoler |b| dans les deux équations.
Pour la première équation :
||\begin{align}-1 &= \log_c (0{,}25b)\\c^{-1} &= 0{,}25b\\ \dfrac{c^{-1}}{0{,}25}&=b \end{align}||
Pour la seconde équation :
||\begin{align}2 &= \log_c (128b) \\ c^{2} &= 128b\\ \dfrac{c^{2}}{128} &= b \end{align}||
On peut maintenant utiliser la méthode de comparaison.
||\dfrac{c^{-1}}{0{,}25} = \dfrac{c^{2}}{128}||
On travaille un peu sur la proportion :
||\begin{align} \dfrac{128}{0{,}25} &= \dfrac{c^2}{c^{-1}}\\ 512 &= c^3\\ \sqrt[3]{512} &= \sqrt[3]{c^3}\\ 8 &= c \end{align}||
On a donc comme base |c=8.|

Il ne reste qu'à remplacer |c| dans l'une des équations de départ pour trouver le |b.|
||b = \dfrac{c^{-1}}{0{,}25} = \dfrac{8^{-1}}{0{,}25} = \dfrac{1/8}{1/4} = \dfrac{1}{2}\\ b = \dfrac{c^2}{128} = \dfrac{8^2}{128} = \dfrac{64}{128} = \dfrac{1}{2}||
Réponse : l'équation de la fonction est donc |y= 4 \log_8 \left(\dfrac{1}{2}(x)\right).|

Lorsqu'on connait la valeur d'un seul paramètre, il faut travailler avec les coordonnées de 2 points qui sont situés sur la courbe. On utilise ensuite la méthode de résolution algébrique par comparaison.

Il y a deux façons d'exprimer la règle d'une fonction logarithmique sous sa forme canonique :

||y= \log_c \big(b(x-h)\big)||

OU

||y= \log_c (\pm(x-h)) + k||

Avec un exemple concret, on obtient :

||\begin{align} y &= \log_c \big(b(x-h)\big) && \text{première forme canonique}\\\\ &= \log_2 \big(-16(x-8)\big) && \text{règle avec laquelle on travaille}\\\\ &= \log_2 16 + \log_2 (-(x-8)) && \text{logarithme d'un produit} \\\\ &= 4 + \log_2 (-(x-8))&& \text{calcul du logarithme}\\\\ &= \log_2 (-(x-8)) + 4 && \text{réarrangement des termes} \\\\ y &= \log_c (\pm(x-h)) + k && \text{deuxième forme canonique} \end{align}||

Lorsqu'on travaille avec une fonction logarithmique, il y a un facteur multiplicatif entre les variations de la variable indépendante lorsque la variable dépendante augmente de 1. Ce facteur multiplicatif correspond à la base |c| de la fonction.

Voici la table de valeurs de la fonction |y=\log_9 x| ainsi que les différentes variations.

On remarque que le facteur multiplicatif est de 9, ce qui correspond à la base |c| de la fonction |y=\log_9 x.|

Voici les étapes à suivre afin de trouver la règle d'une fonction logarithmique sous la forme |y= \log_c \big(\pm(x-h)\big)+k :|

1. Déterminer la valeur de la base |c| en trouvant le facteur multiplicatif.

2. Selon la valeur de la base |c|, on détermine si on utilise le + ou le - dans la parenthèse.

3. Remplacer |x| et |y| dans l'équation de la fonction par 2 couples.

4. Isoler le paramètre |k| dans les deux équations.

5. Utiliser la méthode de résolution algébrique par comparaison afin de trouver la valeur du paramètre |h.|

6. Remplacer |h| dans l'une ou l'autre des deux équations pour déduire la valeur du paramètre |k.|

Voici la table de valeurs d'une fonction logarithmique :

1. Déterminer la valeur de la base |\boldsymbol{c}| en trouvant le facteur multiplicatif.

La base est donc |c=3|.

2. Selon la valeur de la base |\boldsymbol{c,}| on détermine si on utilise le + ou le - à l'intérieur des parenthèses.
   
   Dans le cas présent, plus les valeurs de |x| augmentent, plus celles de |y| diminuent. Puisque la fonction est décroissante et que la valeur de la base |c| est supérieure à 1, on doit utiliser la signe |-| dans les parenthèses. 
   ||\begin{align} y &= \log_{\color{magenta}{c}} (\color{red}{\pm}(x-h))+k\\ y &= \log_{\color{magenta}{3}} (\color{red}{-}(x-h))+k\end{align}||

3. Remplacer |\boldsymbol{x}| et |\boldsymbol{y}| dans l'équation de la fonction par 2 couples.
   
   On peut prendre les couples (0, 2) et (-8, 4) et les insérer dans l'équation. ||\begin{align} 2 &= \log_3 (-(0-h))+k\\ \Rightarrow\ 2 &= \log_3 (h) +k \\\\ 4 &= \log_3 (-(-8-h))+k \\ \Rightarrow\ 4 &= \log_3 (8+h) +k\end{align}||

4. Isoler le paramètre |\boldsymbol{k}| dans les 2 équations.
   
   On obtient alors |2- \log_3 (h) = k| et |4-\log_3 (8+h) = k.|

5. Utiliser la méthode de résolution algébrique par comparaison afin de trouver la valeur du paramètre |\boldsymbol{h.}|

||\begin{align} 2 - \log_{3}{(h)} &= 4 - \log_{3}{(8+h)}\\\\ 2 - 4 &= -\log_{3}{(8+h)} + \log_{3}{(h)} \\\\ -2 &= \log_{3}{(h)} - \log_{3}{(8+h)} && \text{Réarrangement des logarithmes}\\\\ -2 &= \log_{3}\left(\dfrac{h}{8+h}\right) && \text{Logarithme d'un quotient}\\\\ 3^{-2} &= \dfrac{h}{8+h} && \text{Passage à la forme exponentielle}\\\\ \dfrac{1}{3^{2}} &= \dfrac{h}{8+h} && \text{Définition d'un exposant négatif} \\\\ \dfrac{1}{9} &= \dfrac{h}{8+h} \\\\ 8+h &= 9h && \text{Par produit croisé} \\\\ 8 &= 8h \\\\ h &= 1 \end{align}||

6. Remplacer |\boldsymbol{h}| dans l'une ou l'autre des 2 équations pour déduire la valeur du paramètre |\boldsymbol{k.}|

||\begin{align}4 &= \log_3 (-(-8-h))+k \\\\4 &= \log_3 (-(-8-1)) + k && \text{Remplace } h \text{ par sa valeur} \\\\4 &= \log_3 (9) + k\\\\4 &= 2 + k && \text{Calcul du logarithme}\\\\2&=k \end{align}||On peut donc conclure que l'équation de notre fonction logarithmique est : ||y= \log_3 (-(x-1))+2||

1. Remplacer |h| par la valeur de l'asymptote.

2. Substituer chacun des points pour créer un système d'équations.

3. Déterminer la valeur de la base |c| à l'aide de la méthode de comparaison.

4. Utiliser une des deux équations de l'étape 2 pour trouver la valeur du paramètre |b.|

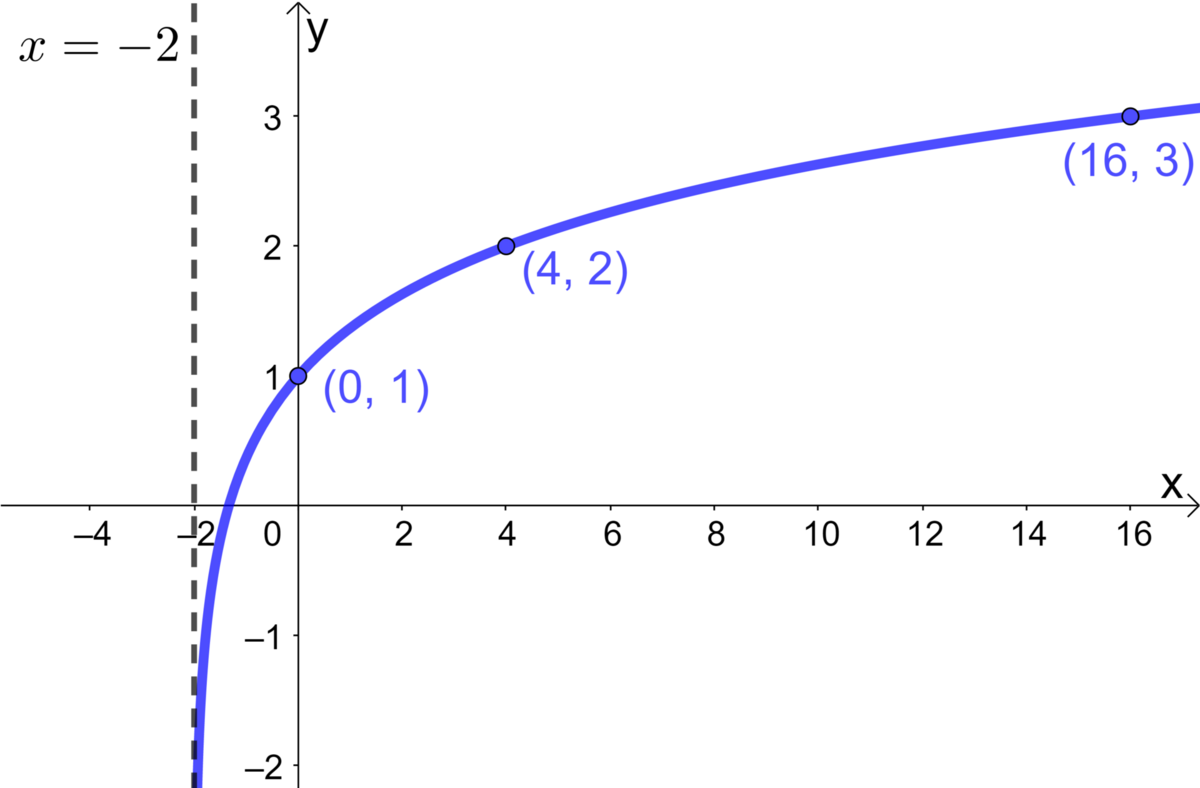
1. Remplacer |\boldsymbol{h}| par la valeur de l'asymptote. ||\begin{align} y &= \log_c \big(b(x-\color{green}{h})\big) \\y &= \log_c \big(b(x-\color{green}{\text{-}2})\big) \\y &= \log_c \big(b(x\color{green}{+2})\big) \\ \end{align}||

2. Substituer chacun des points pour créer un système d'équations.

||\begin{align} &1^{\text{er}}\text{ couple : }(0,1) && 2^{\text{e}}\text{ couple : }(16,3) \\\\ y &= \log_c \big(b(x+2)\big) && y = \log_c \big(b(x+2)\big) \\\\ 1 &= \log_c \big(b(0+2)\big) && 3 = \log_c \big(b(16+2)\big) && \text{Substitue } x \text{ et } y \\\\ 1 &= \log_c (2b) && 3 = \log_c (18b) \\\\ c^1 &=2b && c^3 =18b \\\\ \dfrac{c}{2} &= b && \dfrac{c^3}{18} = b && \text{Isole } b \end{align}||

3. Déterminer la valeur de la base |\boldsymbol{c}| à l'aide de la méthode de comparaison.

||\begin{align} b & = b \\\\ \frac{c}{2} & = \frac{c^3}{18} \\\\ \frac{18}{2} & = \frac{c^3}{c} \\\\ 9 & = c^2 && \text{propriétés des exposants}  \\\\ \sqrt9 & = \sqrt{c^2} \\\\ 3 & = c\end{align}||

4. Utiliser une des deux équations de l'étape 2 pour trouver la valeur du paramètre |\boldsymbol{b}.| ||b = \dfrac{c}{2} = \dfrac{3}{2} = 1{,}5||

On conclut en donnant l'équation de la fonction logarithmique : ||y = \log_3 \big(1{,}5(x+2)\big)||

1. Déduire la valeur du paramètre |b.|

2. Remplacer les coordonnées |(x,y)| dans l'équation.

3. Déterminer la valeur de la base |c.|

Déterminez l'équation de la fonction logarithmique ayant les caractéristiques suivantes :

• L'équation de l'asymptote est |x=-1|

• Son abscisse à l'origine est |-\dfrac{1}{2}|

• Elle passe par le point |(4,1)|

1. Déduire la valeur du paramètre |\boldsymbol{b.}|
   
   En connaissant la valeur du paramètre |h| et l'abscisse à l'origine, on peut trouver celle du paramètre |b.| ||\begin{align} \dfrac{1}{b} + h & = \text{abscisse à l'origine} \\\\ \dfrac{1}{b} -1 &= -\dfrac{1}{2}\\\\ \dfrac{1}{b} &= \dfrac{1}{2} \\\\ b &=2 \end{align}||

2. Remplacer les coordonnées |\boldsymbol{(x,y)}| dans l'équation.
   
   Puisqu'on sait que la courbe passe par |(4,1),| on obtient : ||\begin{align} y & = \log_c \big(2(x+1)\big) \\ 1 &= \log_c \big(2(4+1)\big)\end{align}||

3. Déterminer la valeur de la base |\boldsymbol{c.}|
   
   Selon l'équation obtenue précédemment, ||\begin{align}1&= \log_c \big(2(4+1)\big) \\c^1 &= 2(4+1)\\c^1 &= 10 \\c & = 10 \end{align}||

Réponse : L'équation de la fonction est |y= \log_{10} \big(2(x+1)\big).|