Bonjour,
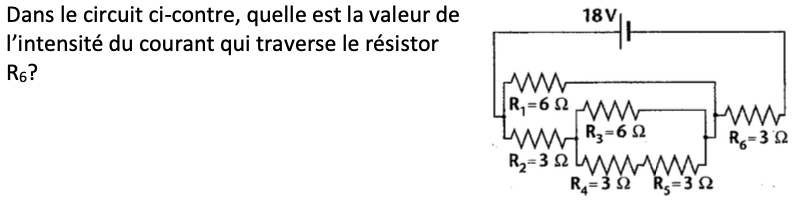
J'ai un problème concernant les lois de kirchhoff, que voici:
Je comprend quelles sont les étapes pour y arriver. Toutefois, je n'arrives pas à calculer la résistance équivalente. J'ai essayé à plusieurs reprise, mais je n'ai jamais la même réponse que dans le corrigé. Le corrigé me dit que la résistance équivalente est de 6 ohm. Donc, j'aimerais savoir comment celui ou celle qui à fait le corrigé a pus trouver 6 ohm.
Merci d'avance et bonne journée à tous,
Explication (1)
Explication d’élève
12 mai 2021
Salut ! :)
Merci pour ta question!
L'essentiel du problème consiste à utiliser les règles des résistances équivalentes en ordre. Ainsi, il faut commencer par les résistances qui sont les plus nichées au sein de circuits en série en parallèle. En l'occurence, il s'agit de R4 et R5 (entourées par le cercle bleu dans le schéma ci-dessous).
Une fois que la résistance équivalente à R4 et R5 a été trouvée, on peut s'imaginer R4 et R5 comme étant remplacées par une résistance (appelons la R4-5).
Dès lors, il est possible de trouver la résistance équivalente entre R4-5 et R3 (entourées par le cercle vert).
On répète le même processus de remplacement que dans la première étape et on poursuit avec les autres cercles concentriques, jusqu'à ce qu'on trouve une résistance équivalente pour tout le circuit.
Rappelle toi que lorsque les résistances sont placées en série (au sein d'une branche), la résistance équivalente égale à :
$$ R_{éq}=R_1+R_2+R_3+... $$
Lorsque les résistances sont placées en parallèle, la résistance équivalente égale à :
$$ \frac{1}{R_{éq}} = \frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+... $$
(J'ai testé cette méthode, et elle aboutit à la réponse de 6 Ω).
Cette fiche du site d'Alloprof parle des résistances équivalentes :
Cette fiche du site d'Alloprof parle des calculs dans les circuits électriques :
Voilà!
N'hésite pas si tu as d'autres questions!
En effaçant cette explication, vous supprimerez aussi définitivement la question. Voulez-vous continuer?