Secondary IV • 1yr.
J’ai pour devoir de résoudre ce numéro, mais je ne comprends pas comment le faire, je n’arrive même pas à comprendre le corriger. C’est sur les inéquations (<,>). Merci d’avance. Problème sur photo vierge et corriger.





Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut BromeSigma7358,
Merci pour ta question!
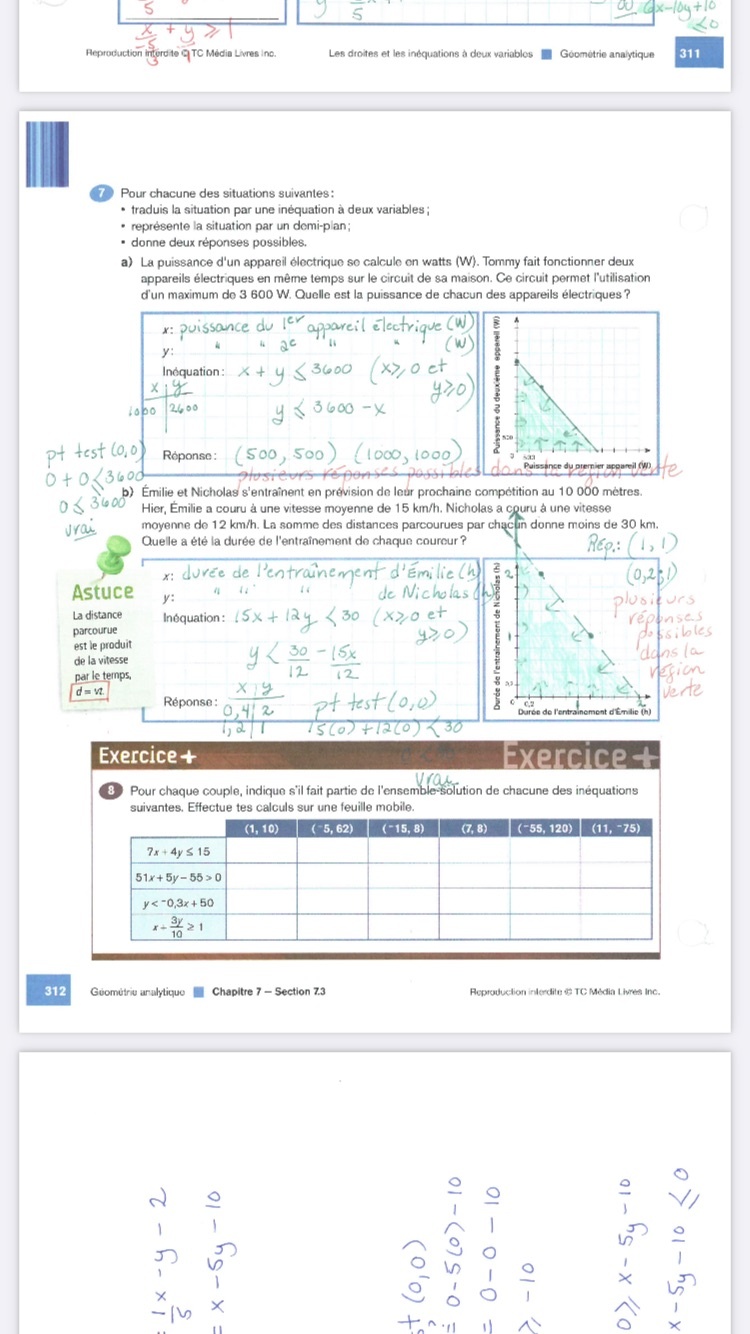
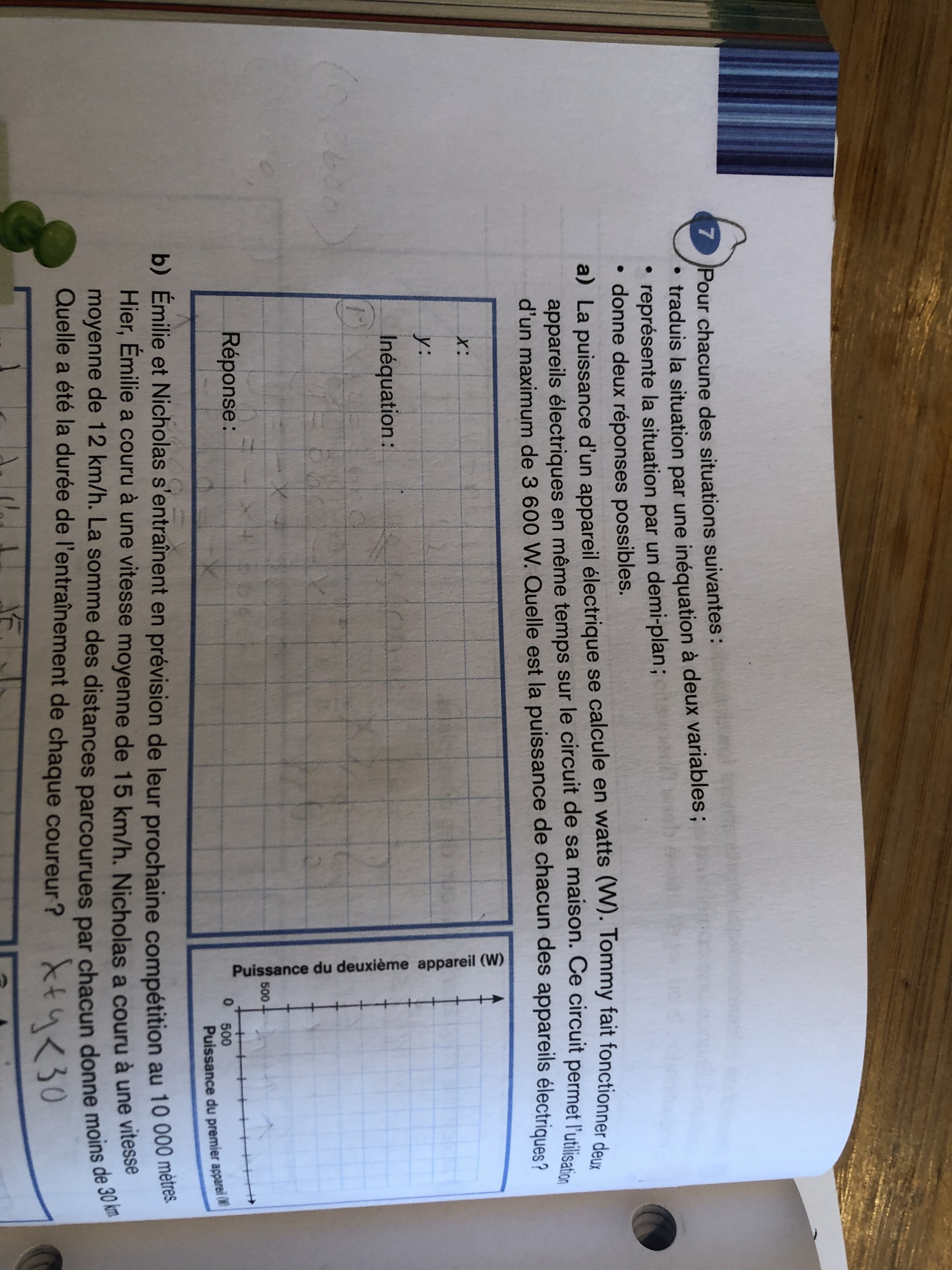
Pour résoudre ces problèmes, tu dois identifier l'inéquation de l'énoncé et la tracer dans un plan cartésien. Regardons la question A ensemble.
On te dit que deux appareils électriques fonctionnent en même et que la puissance maximale de la combinaison de ces deux appareils est de 3600W.
Dans cette situation, on ne connait pas la valeur de la puissance de chaque appareil. On peut donc poser des variables, x et y, pour représenter la puissance des deux appareils. Ainsi, la somme de ces puissances est inférieure ou égale à 3600W, ce qui nous donne l'inéquation suivante :
$$x+y \leq 3600$$
Tu peux tracer cette inéquation dans le plan cartésien. La difficulté est de savoir de quel côté de la droite tu dois ombrager. Lorsqu'on ombrage une section, il s'agit de l'endroit qui valide l'inéquation. Dans ton cas, il s'agit des couples x et y dont la somme est inférieure à 3600.
Pour savoir de quel côté tu dois ombrager, il te suffit de prendre un point et de le tester. Si l'inéquation est vérifiée, le point est dans la section ombragée et si l'inéquation n'est pas vérifiée, le point n'est pas validé.
Une fois que tu as la section ombragée, il ne te reste plus qu'à donner deux points de cette section pour compléter le problème. Ces deux points sont des solutions qui respectent l'inéquation.
Si tu veux en savoir plus à ce sujet, voici notre fiche sur les problèmes de ce genre :
J'espère que ça t'aide et n'hésite pas à nous réécrire si tu as d'autres questions!
Anthony B.