Postsecondary • 10mo.
Salut, j'ai besoin d'aide avec cette question svp. Je n'arrive pas a le faire.
1)Trouvez l'equation de la tangente T a la courbe de f au point P(2, f(2)).
2)
Considérez l’intervalle [2, 4], calculez Δy et dy et identifiez-les sur le graphique.
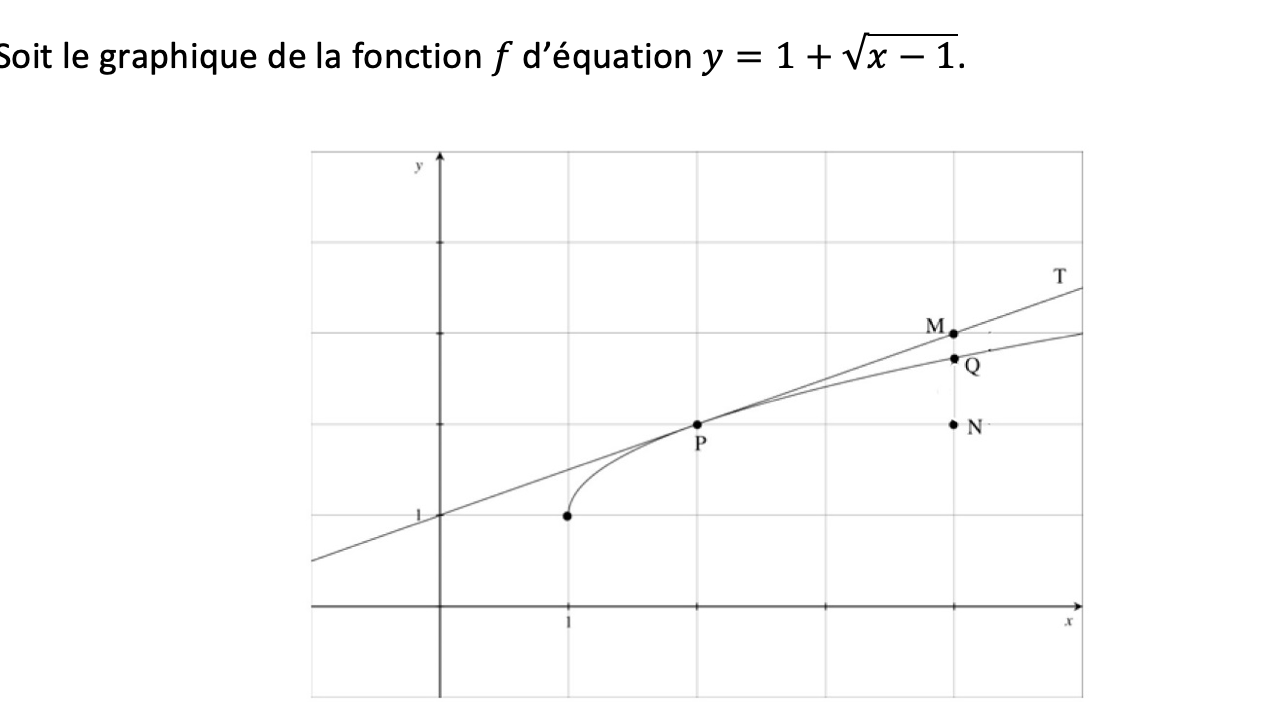





1)
2)
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Explanation from Alloprof
This Explanation was submitted by a member of the Alloprof team.
Salut!
La tangente à une courbe en un de ses points est une droite qui « touche » la courbe à ce point là. Voici une animation qui pourrait t'aider à mieux comprendre : Tangente Animation - YouTube
Pour trouver la pente d'une tangente à un point, il suffit de calculer la dérivée de la règle de la fonction :
Le résultat sera une fonction, notée f'(x), qui donne la pente de la tangente à un point x de la courbe f(x). Ainsi, tu n'auras qu'à calculer f'(2) pour trouver la pente de la tangente au point P x=2.
Puis, pour trouver l'ordonnée à l'origine de la droite (b dans y=ax+b), tu peux utiliser le point (2, f(2)). Tu devras donc d'abord calculer f(2), l'ordonnée du point P, comme ceci :
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)