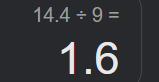Best Of

est ce que on toujoure oubliger de faire des trace de calcul dans les examen

dans fin lapin on me haque tous le temps

comment place un nomber sur une droite numerique ?

Salut!

Merci de faire appel à nos services! :) 

Malheureusement, ta question dépasse les notions vues au primaire et au secondaire.

Voici tout de même deux sources qui pourraient t'être utiles : 

Si tu étudies au collégial ou à l'université, je t'invite à prendre rendez-vous avec la personne qui enseigne ton cours. Les moments de disponibilité sont normalement indiqués sur le plan de cours reçu au début de la session! Ils sauront certainement t'aider à surmonter ces difficultés! :)

J'espère que cela t'aide malgré tout! :)

Salut!

Oui, tu as fait la bonne chose! :) Tu dois transformer les nombres périodiques en fractions.

(PS Attention, on te demande de mettre des nombres rationnels en fraction, et non des nombres irrationnels, puisqu'on ne peut pas mettre des nombres irrationnels en fraction)

Pour cela, tu dois suivre ces étapes :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Par exemple, pour le a), voici la démarche à suivre :

Étape 1 :

$$n=3,\overline{14}$$

Étape 2 :

$$ n \times 100 = 3,\overline{14} \times 100 $$

$$ 100n = 314,\overline{14} $$

Étape 3 : Soustraire le nombre de l'étape 1 du nombre de l'étape 2 pour obtenir un entier.

$$ 100n -n= 314,\overline{14}- 3,\overline{14}$$

$$ 99n= 311$$

Étape 4 : On isole la variable et on simplifie la fraction

$$ \frac{99n}{99}= \frac{311}{99}$$

$$n= \frac{311}{99}$$

On trouve donc que \(3,\overline{14}=\frac{311}{99}\) (et non 311/99n).

Aussi, tu ne dois pas avoir de nombre décimal dans ta fraction finale. Par exemple, au numéro b), la bonne réponse est 15/9.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Pour vérifier si tu as la bonne réponse, je te conseille d'utiliser ta calculatrice. Si tu divises le numérateur par le dénominateur de ta fraction, tu dois obtenir le nombre périodique de départ.

Par exemple, on peut vérifier ta réponse au numéro b comme ceci :

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

On trouve 1,6, et non \(1,\overline{6}\), donc on peut conclure que la réponse trouvée n'est pas la bonne.

Je te laisse corriger le reste des exercices. Tu peux suivre la même démarche expliquée précédemment pour résoudre les numéros.

Aussi, je te conseille de jeter un coup d'œil à cette fiche, tu y trouveras des exemples similaires qui pourront t'aider :

J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)

On te demande de mettre des nombres rationnels en fraction car on ne peut pas mettre des nombres irrationnels en fraction.

L'idée ici est de poser x = le nombre rationnel à mettre en fraction (x= n/m où n et m sont des nombres entiers)

Ensuite tu multiplies ce x pour une puissance de 10 correspondant à la période du nombre décimal

Au numéro 2a) la période est de 2 décimales donc le multiple sera 100

si 100 ou 10² est multiplié à x , on lui soustrait x

100x - x comme dans ton numéro 2a)

c'est un petit subterfuge qui donne un nombre entier n, dans l'exercice 2a) le n = 311

or 100x - x = 99x

on a donc 99x = 311

c'est-à-dire x = 311/99 le nombre rationnel sous forme de fraction

Pour t'assurer que tu as bien trouvé la bonne réponse, tu n'as qu'à effectuer la division.

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.