Les équations des miroirs

Certains éditeurs utilisent la variable $p$ pour représenter la distance objet-miroir et la variable $q$ pour représenter la distance image-miroir. Ces variables sont semblables à des variables définies ci-dessus: $p$ est équivalent à $d_{o}$, alors que $q$ est équivalent à $d_{i}$.

Le grandissement ($G$) ou le grossissement d'un objet est le rapport de la grandeur de l’image ($h_{i}$) sur la grandeur de l’objet ($h_{o}$).

Pour calculer le grandissement, la formule à utiliser est la suivante:
$G=\displaystyle \frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} = \frac {-l_{f}}{l_{o}} = \frac {-l_{i}}{l_{f}}$

Les formules à utiliser dans les miroirs courbes sont les suivantes:
$G=\displaystyle \frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} = \frac {-l_{f}}{l_{o}} = \frac {-l_{i}}{l_{f}}$

$\displaystyle \frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}}$

${d_{i}} = {l_{i}} + {l_{f}}$

${d_{o}} = {l_{o}} + {l_{f}}$

${l_{i}} \times {l_{o}} = {l_{f}}^2$

$R = 2 \times {l_{f}}$

Les formules dans les miroirs courbes n'utilisent pas d'unités précises. Toutes les mesures représentent des mesures de longueur qui peuvent être mesurées par des mètres ou des centimètres. Bien que le choix des unités reste vaste, il est important de convertir toutes les mesures afin d'avoir les mêmes unités de mesure.

Un objet de $\small \text {5,0 cm}$ de hauteur est placé $\small \text {25 cm}$ devant un miroir concave (convergent) dont la longueur focale est de $\small \text {10 cm}$.  À quelle distance du miroir se positionnera l’image et quelle en sera sa taille ?

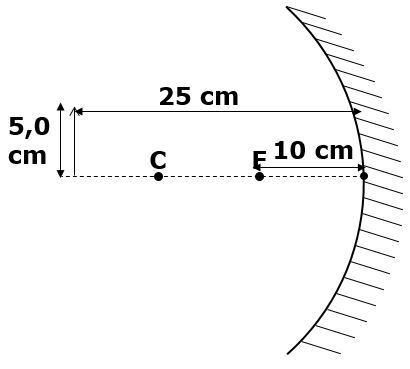
Voici les informations connues dans ce problème.
$$\begin{align} h_{o} &= 5,0\:\text{cm} &d_{o} &= 25 \: \text{cm}\\ l_{f} &= 10 \: \text {cm} \\ d_{i} &= \: ?  &h_{i} &= \: ? \\ \end{align}$$
Pour trouver la distance image-miroir, la formule suivante est utilisée:
$$\begin{align} \frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}} \quad \Rightarrow \quad \frac {1}{25 \: \text {cm}} + \frac {1}{d_{i}} &= \frac {1}{10\: \text {cm}} \\ 0,04 + \frac {1}{d_{i}} &= 0,10 \\ \frac {1}{d_{i}} &= 0,06 \\ {d_{i}} &= 17 \: \text {cm}\\ \end{align}$$
La réponse obtenue a un signe positif: ceci signifie que l'image est réelle.

Pour trouver la hauteur de l'image, il faut utiliser les proportions présentes dans la formule du grandissement.
$$\begin{align} \frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} \quad \Rightarrow \quad {h_{i}} &= \frac {h_{o} \times -d_{i}}{d_{o}} \\ {h_{i}} &= \frac {{5,0 \: \text {cm}}  \times -(17 \: \text {cm})}{25 \: \text {cm}} \\ {h_{i}} &= -3,4 \: \text {cm} \end{align}$$
Le signe négatif indique que l'image est inversée.

Les caractéristiques de  l'image sont les suivantes: elle est réelle, inversée, plus petite que l'objet (car $h_{i} < h_{o}$) et entre F et C (puisque le centre de courbure est situé à $2 \times l_{f}$, soit $20 \text { cm}$).

On place un objet de $\small \text {4,2 cm}$ de hauteur à $\small \text {10 cm}$ devant un miroir convexe de longueur focale inconnue. L'image mesure $\small \text {1,4 cm}$ de hauteur. Détermine la longueur focale de ce miroir.

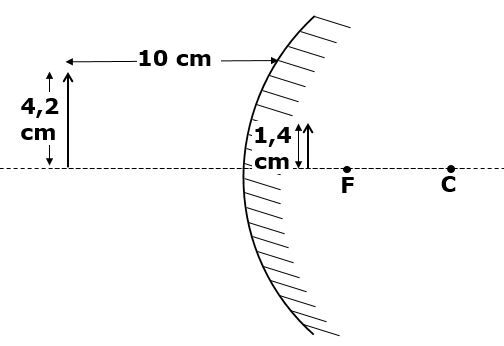
Voici les informations connues dans ce problème.
$$\begin{align} h_{o} &= 4,2\:\text{cm} &d_{o} &= 10 \: \text{cm}\\ h_{i} &= +1,4 \: \text {cm} &l_{f} &= \: ?  \\ \end{align}$$
Puisque le miroir est convexe, les images sont toujours droites: la valeur de la hauteur de l'image est donc nécessairement positive.
Étant donné qu'il n'est pas possible de déterminer immédiatement la valeur de $l_{f}$, il faut auparavant trouver une autre valeur, soit celle de $d_{i}$.
$$\begin{align} \frac {h_{i}}{h_{o}} = \frac {-d_{i}}{d_{o}} \quad \Rightarrow \quad {d_{i}} &= \frac {-h_{i} \times d_{o}}{h_{o}} \\ {d_{i}} &= \frac {{-1,4 \: \text {cm}}  \times 10 \: \text {cm}}{4,2 \: \text {cm}} \\ {d_{i}} &= -3,3 \: \text {cm} \end{align}$$
La valeur négative était prévisible, puisque les miroirs divergents produisent en tout temps des images virtuelles.

Finalement, il est possible de déterminer la longueur focale en utilisant l'une des formules décrites ci-dessus.
$$\begin{align} \frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}} \quad \Rightarrow \quad \frac {1}{l_{f}} &= \frac {1}{10 \: \text {cm}} + \frac {1}{- 3,3 \: \text {cm}} \\ \frac {1}{l_{f}} &= 0,1  - 0,3 = \frac {1}{l_{f}} \\ \frac {1}{l_{f}} &= -0,2\\ {l_{f}} &= -5 \: \text {cm} \end{align}$$
La longueur focale du miroir convexe est de $\text {5 cm}$. La valeur négative indique que le miroir est bel et bien divergent.

Quelle est la distance objet-miroir dans un miroir convexe ayant une longueur focale de $\small \text {20,0 cm}$ si le grossissement est $\small \text {0,25}$ ?

Voici les informations connues dans ce problème.
$$\begin{align} l_{f} &= -20,0\:\text{cm} &G &= 0,25\\ d_{o} &= \: ? &d_{i} &= \: ?  \\ \end{align}$$
Pour trouver la valeur de $d_{o}$, il faut utiliser le grossissement pour déterminer la relation entre la $d_{o}$ et $d_{i}$.

$$\begin{align} G=\displaystyle \frac {-d_{i}}{d_{o}} \quad \Rightarrow \quad 0,25 &=\displaystyle \frac {-d_{i}}{d_{o}} \\ -0,25 \times {d_{o}} &= {d_{i}} \end{align}$$

Pour trouver la distance objet-miroir, la formule suivante est utilisée.

$$\begin{align} \frac {1}{d_{o}} + \frac {1}{d_{i}} = \frac {1}{l_{f}} \quad \Rightarrow \quad \frac {1}{d_{o}} - \frac {1}{0,25 \times {d_{o}}} &= \frac {1}{-20,0 \: \text {cm}}\\ \frac {0,25}{0,25 \times d_{o}} - \frac {1}{0,25 \times {d_{o}}} &= \frac {1}{-20,0 \: \text {cm}}\\ \frac {-0,75}{0,25 \times d_{o}}&= \frac {1}{-20,0 \: \text {cm}}\\ {(-0,75)}{(-20,0 \: \text {cm})}&=0,25 \times d_{o} \\ {15 \: \text {cm}}&=0,25 \times d_{o}\\ 60 \: \text {cm} &= d_{o} \end{align}$$