
Le rôle des paramètres dans une fonction tangente
Secondaire 5
Lorsqu’on ajoute les paramètres a, b, h et k à la forme de base f(x)=tan(x), on obtient ce qu'on appelle la forme canonique (aussi appelée forme transformée) de la fonction tangente.
La forme canonique d'une fonction tangente est : f(x)=atan(b(x−h))+koù a, b, h et k sont des nombres réels jouant le rôle de paramètres.
Remarque : Les paramètres a et b sont toujours différents de zéro.
Manipulation animée des paramètres
Dans l'animation suivante, tu peux modifier les paramètres a, b, h et k de la fonction tangente. Observe bien les modifications qui s'opèrent sur la courbe transformée (en noir) par rapport à la fonction de base (en orange). Tu peux même en profiter pour observer l'effet de la modification des paramètres sur les propriétés de la fonction. Par la suite, tu pourras poursuivre la lecture de la fiche pour avoir toutes les précisions sur chacun des paramètres.
L'analyse du paramètre a
Un changement d'échelle vertical de la courbe de facteur a
Lorsque ∣a∣>1:
Lorsque la valeur absolue de a augmente, les couples de la fonction ont tendance à être de plus en plus éloignés de l'axe horizontal. On observe un allongement vertical de la fonction par rapport à la fonction de base.
Lorsque 0<∣a∣<1:
Lorsque la valeur absolue de a se rapproche de 0, les couples de la fonction ont tendance à se rapprocher de l'axe horizontal. On observe un rétrécissement vertical de la fonction par rapport à la fonction de base.
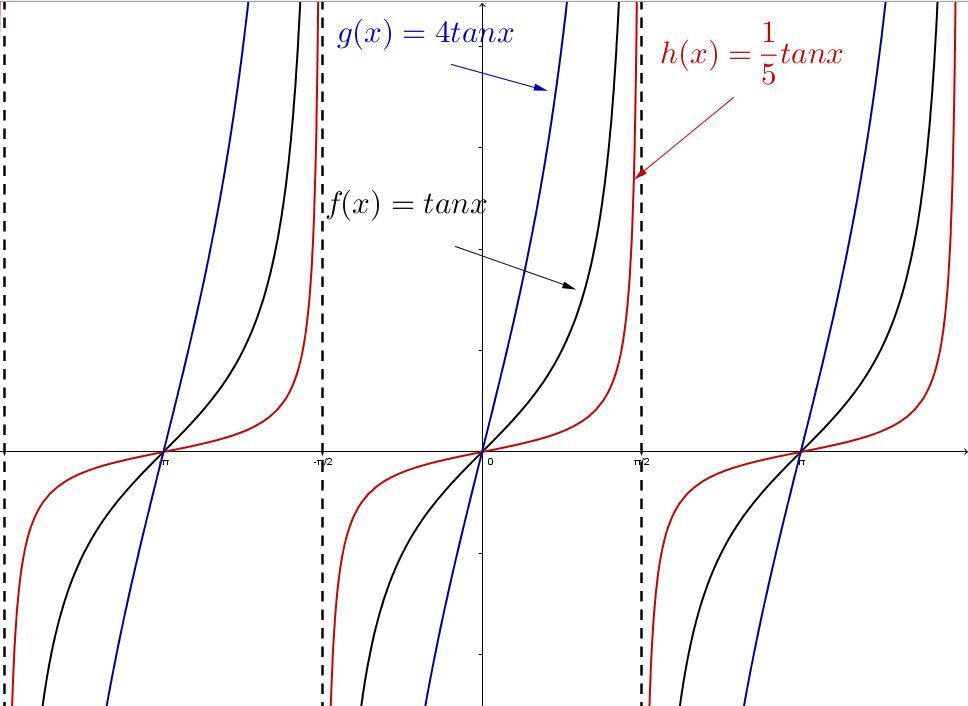
Une réflexion du graphique de la fonction autour de l'axe des x
Le paramètre a est aussi responsable de l’orientation du graphique de la fonction tangente.
Lorsque a est négatif (a<0):
La fonction subit une réflexion par rapport à l’axe des x.
L'analyse du paramètre b
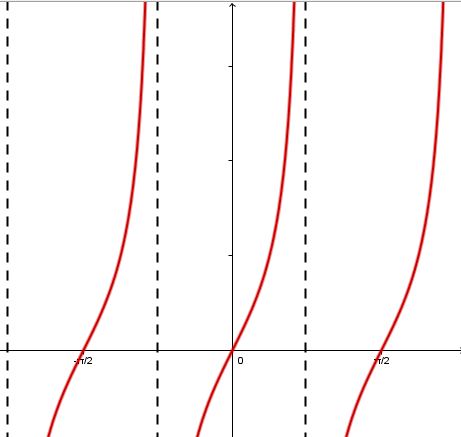
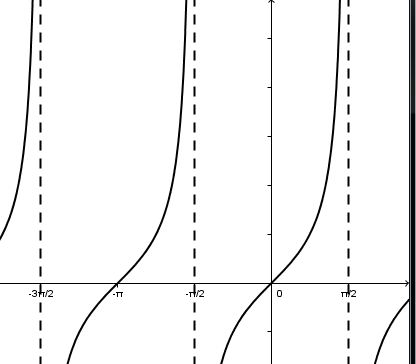
Un changement d'échelle horizontal de la courbe de facteur 1b
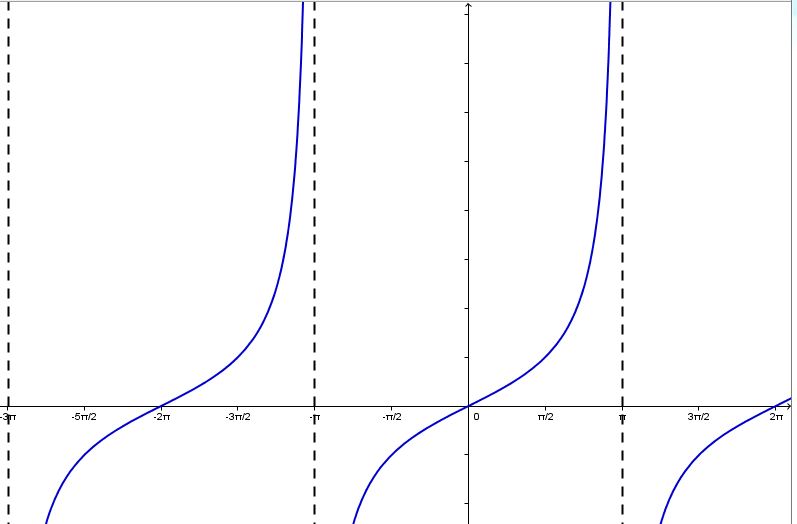
Lorsque ∣b∣>1:
Plus la valeur absolue de b est grande, plus la période est petite. La distance entre deux zéros de la fonction devient plus petite.
Lorsque 0<∣b∣<1:
Plus la valeur absolue de b est petite (près de 0), plus la période est grande. La distance entre deux zéros de la fonction devient plus grande.
| g(x)=tan(2x) p=π2 |
f(x)=tan(x) p=π |
h(x)=tan(12x) p=2π |
|---|---|---|
 |
 |
 |
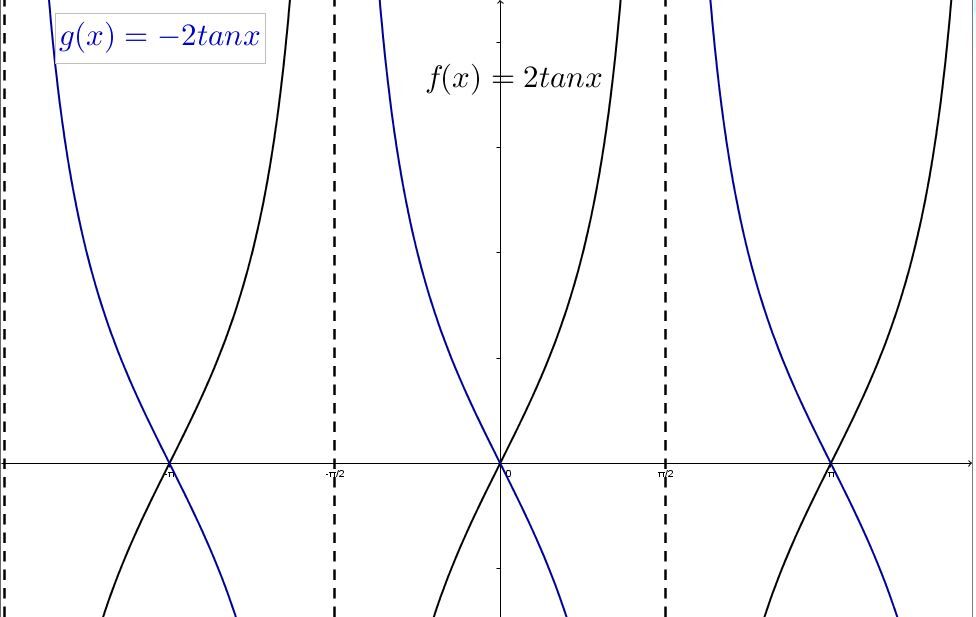
Une réflexion du graphique de la fonction autour de l'axe des y
Le paramètre b est aussi responsable de l’orientation du graphique de la fonction tangente.
Lorsque b est négatif (b<0):
La fonction subit une réflexion par rapport à l’axe des y.

La combinaison des paramètres a et b
La variation de la courbe
Puisque la courbe d'une fonction tangente peut subir des réflexions, le signe des paramètres a et b permet de prédire la croissance ou la décroissance de la courbe de la fonction entre deux asymptotes.
Lorsque a et b sont du même signe (ab>0):
La fonction est croissante entre deux asymptotes.
Lorsque a et b sont de signes contraires (ab<0):
La fonction est décroissante entre deux asymptotes.
L'analyse du paramètre h
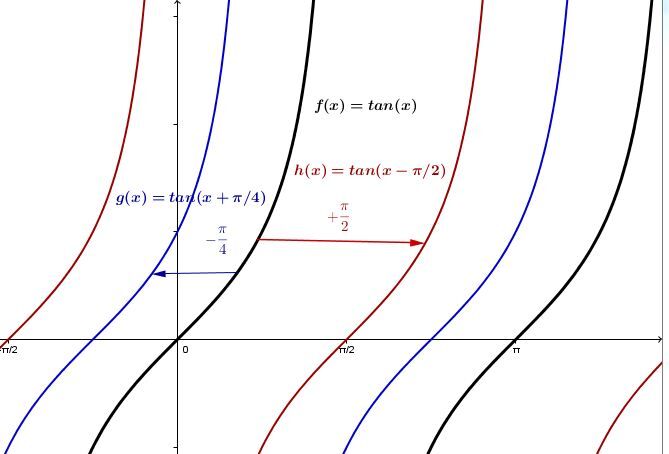
Une translation horizontale de toute la fonction
Le paramètre h est responsable du déplacement horizontal de la courbe. C’est ce qu’on appelle aussi le déphasage dans une fonction périodique.
Lorsque h est positif (h>0):
La courbe de la fonction tangente se déplace vers la droite.
Lorsque h est négatif(h<0):
La courbe de la fonction tangente se déplace vers la gauche.
L'analyse du paramètre k
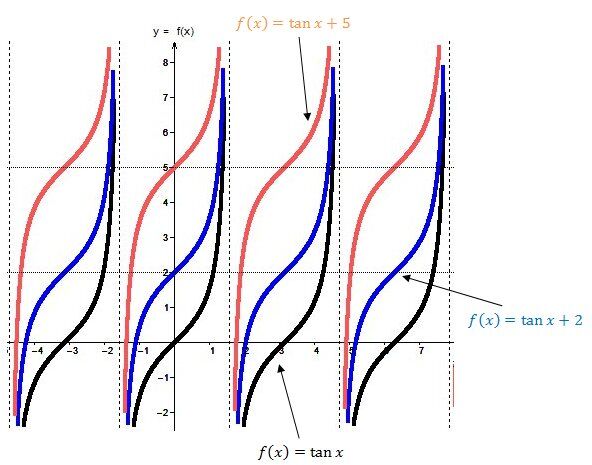
Une translation verticale de toute la fonction
Lorsque k est positif (k>0):
La courbe de la fonction tangente se déplace vers le haut.
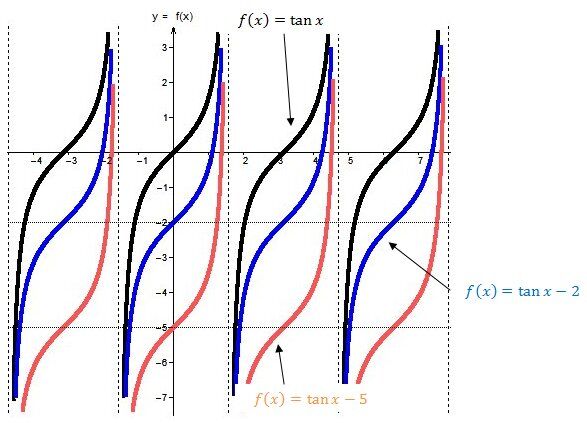
Lorsque k est négatif (k<0):
La courbe de la fonction tangente se déplace vers le bas.
Dans cette page
- Haut de page
- Manipulation animée des paramètres
- L'analyse du paramètre a
- Un changement d'échelle vertical de la courbe de facteur a
- Une réflexion du graphique de la fonction autour de l'axe des x
- L'analyse du paramètre b
- Un changement d'échelle horizontal de la courbe de facteur 1b
- Une réflexion du graphique de la fonction autour de l'axe des y
- La combinaison des paramètres a et b
- La variation de la courbe
- L'analyse du paramètre h
- Une translation horizontale de toute la fonction
- L'analyse du paramètre k
- Une translation verticale de toute la fonction
- À voir aussi















































