Le cercle (conique)
Le cercle fait partie des coniques. Il s’obtient par l’intersection d’une surface conique et d’un plan.
Le cercle est le lieu géométrique de tous les points situés à égale distance d’un point nommé centre.
Le cercle centré à l'origine
L’équation du cercle centré à l’origine
Tout point |(x,y)| qui appartient au cercle peut être trouvé grâce au théorème de Pythagore (aussi appelé relation de Pythagore).
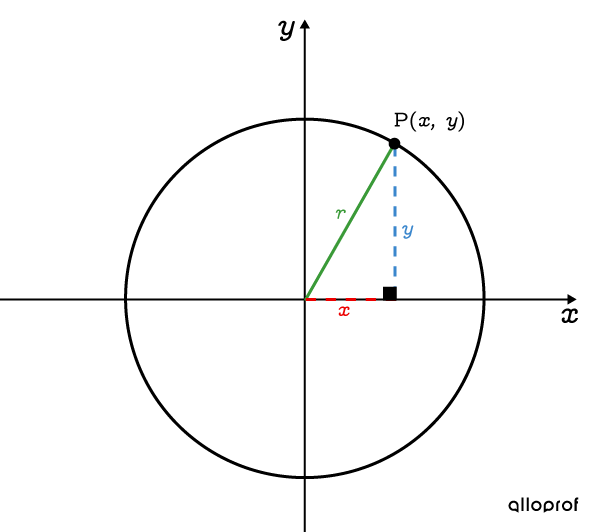
L'équation qui définit le cercle centré à l’origine utilise le paramètre |r.|
||x^2+ y^2= r^2||
où
||r=\text{rayon du cercle}||
Déterminer l’équation d’un cercle centré à l’origine
Pour déterminer l’équation d’un cercle centré à l’origine, il faut trouver la valeur du rayon |r.|
Règle
-
Déterminer la valeur du paramètre |\color{#3a9a38}r,| le rayon du cercle. Au besoin, substituer |x| et |y| par un point du cercle et résoudre l'équation.
-
Écrire l'équation du cercle.
Détermine l’équation du cercle centré à l’origine qui passe par le point |(7,-3).|
Voir la solution
Tracer un cercle centré à l’origine à l’aide de son équation
Règle
-
Placer le centre du cercle à l’origine du plan cartésien.
-
Déterminer le paramètre |\color{#3a9a38}r| à l’aide de l'équation.
-
Avec un compas, tracer à partir du centre un cercle dont le rayon est égal à |\color{#3a9a38}r.|
Trace le cercle d’équation |x^2+y^2=36.|
Voir la solution
Le cercle non centré à l'origine
L’équation du cercle non centré à l’origine
Même si le cercle n'est pas centré à l'origine, on peut tout de même utiliser le théorème de Pythagore pour tout point |(x,y)| qui appartient au cercle.
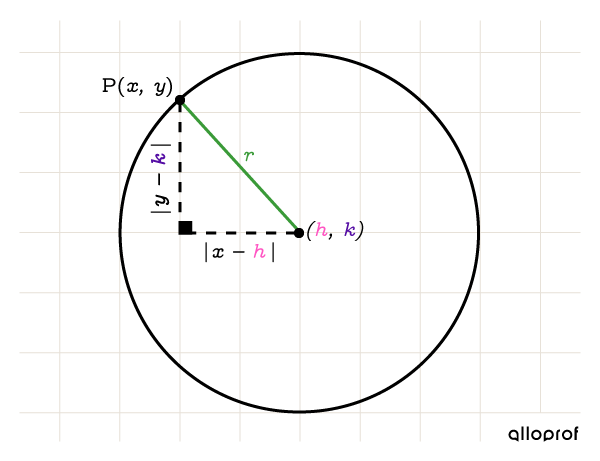
L'équation qui définit le cercle non centré à l’origine utilise les paramètres |r,| |h| et |k.|
||(x-h)^2+(y-k)^2= r^2||
où
||\begin{align} r&=\text{rayon du cercle}\\ (h,k)&=\text{coordonnées du centre du cercle}\end{align}||
Déterminer l’équation d’un cercle non centré à l’origine
Pour déterminer l’équation d’un cercle non centré à l’origine, il faut trouver la valeur du rayon |r| et des coordonnées |(h, k)| du centre.
Règle
-
Déterminer la valeur des paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| à partir des coordonnées du centre du cercle.
-
Déterminer la valeur du paramètre |\color{#3a9a38}r,| le rayon du cercle. Au besoin, substituer |x| et |y| par un point du cercle et résoudre l'équation.
-
Écrire l’équation du cercle.
Détermine l'équation d'un cercle qui passe par les points |(-1, 0)| et |(-1, 4).|
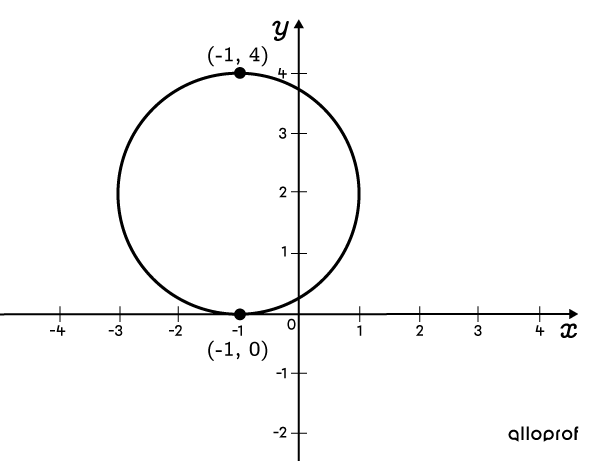
Voir la solution
Tracer un cercle non centré à l’origine à l’aide de son équation
Règle
-
Identifier les paramètres |\color{#FF55C3}h| et |\color{#560FA5}k| dans l'équation et placer le centre du cercle.
-
Déterminer le paramètre |\color{#3a9a38}r| dans l'équation.
-
Avec un compas, tracer à partir du centre un cercle dont le rayon est égal à |\color{#3a9a38}r.|
Trace le cercle d’équation |(x+4)^2+(y-3)^2=16.|
Voir la solution
L'inéquation du cercle
Lorsqu'on veut représenter une région délimitée par un cercle, on applique les relations suivantes.
| Secteur du plan | Représentation graphique | Inéquation correspondante |
|---|---|---|
|
L'extérieur, excluant la courbe |
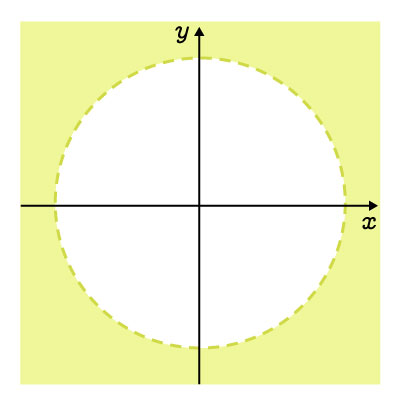 |
||\begin{align}x^2&+y^2>r^2\\\\(x-h)^2&+(y-k)^2>r^2\end{align}|| |
|
L'intérieur, excluant la courbe |
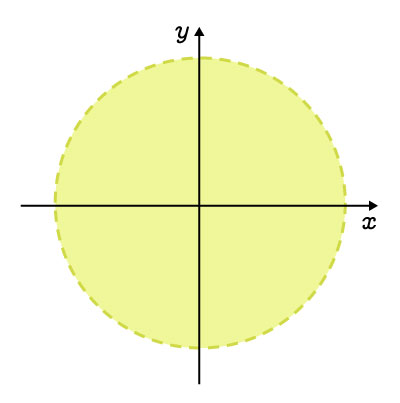 |
||\begin{align}x^2&+y^2<r^2\\\\(x-h)^2&+(y-k)^2<r^2\end{align}|| |
|
L'extérieur du cercle, incluant la courbe |
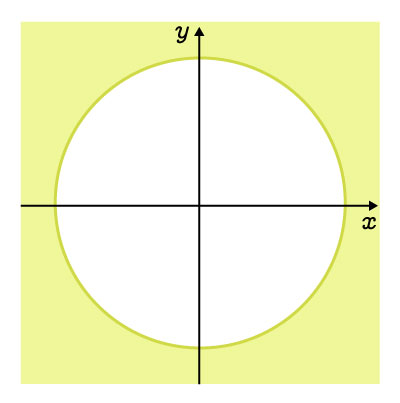 |
||\begin{align}x^2&+y^2\geq r^2\\\\(x-h)^2&+(y-k)^2\geq r^2\end{align}|| |
|
L'intérieur du cercle, incluant la courbe |
 |
||\begin{align}x^2&+y^2\leq r^2\\\\(x-h)^2&+(y-k)^2\leq r^2\end{align}|| |
Trouver l'équation de la tangente à un cercle
Une tangente à un cercle est une droite perpendiculaire au rayon qui passe au point de tangence.
Règle
-
Déterminer la pente de la droite passant par le centre du cercle et le point de tangence.
-
Déterminer la pente de la tangente grâce à la relation entre 2 droites perpendiculaires.
-
Déterminer l’ordonnée à l’origine de la tangente à l’aide de sa pente et des coordonnées du point de tangence.
-
Écrire l’équation de la droite tangente.
Détermine l'équation de la tangente au cercle d'équation |(x+1)^2+(y-2)^2=25| au point |(2,6).|
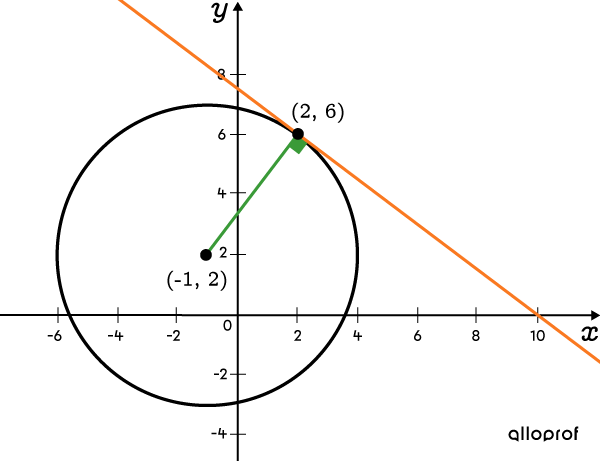
Voir la solution
L’équation du cercle sous forme générale
L'équation générale de toutes les coniques, dont le cercle, pour lesquelles l'axe horizontal est parallèle à l'axe des abscisses et l'axe vertical est parallèle à l'axe des ordonnées est || Ax^2+ By^2+Cx+Dy+E=0.||
- Haut de page
- Le cercle centré à l'origine
- Déterminer l’équation d’un cercle centré à l’origine
- Tracer un cercle centré à l’origine à l’aide de son équation
- Le cercle non centré à l'origine
- L’équation du cercle non centré à l’origine
- Tracer un cercle non centré à l’origine à l’aide de son équation
- L'inéquation du cercle
- Trouver l'équation de la tangente à un cercle
- L’équation du cercle sous forme générale
- À voir aussi
















































