La résolution de systèmes d'équations de degré 1 et de degré 2 (semi-linéaires)

1. Égaler les deux équations à l'aide de la méthode de comparaison.
   
   Si l'équation de la parabole n'est pas sous la forme $y=ax^2+bx+c$, il faut la ramener sous cette forme. De plus, si l'équation de la droite n'est pas sous la forme $y=ax+b$, il faut la ramener sous cette forme.

2. Envoyer tous les termes du même côté de l'égalité afin d'avoir l'un des deux membres égal à 0. À partir de là, on peut déterminer le nombre de solutions.
   
   En effet, avec $ax^2+bx+c=0$ et selon la valeur de $b^2-4ac$ on peut trouver le nombre de solutions.

• Si $b^2-4ac<0,$ il n'y a aucune solution.

• Si $b^2-4ac=0,$ il y a une seule solution.

• Si $b^2-4ac>0,$ il y a deux solutions.

3. Factoriser (si possible) ou utiliser la formule quadratique afin de trouver la ou les solutions en $x.$

4. Trouver la ou les solutions en $y.$

5. Donner le ou les couples solutions.

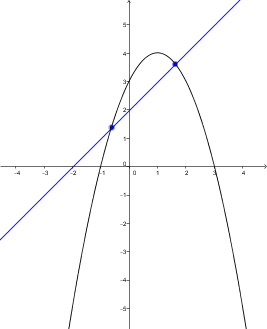
Soit le système d'équations suivant : $$\begin{cases}y=-x^2+2x+5\\y=x+3\end{cases}$$

1. On peut écrire l'égalité $-x^2+2x+5=x+3.$

2. On envoie tous les termes du même côté de l'égalité. Dans ce cas-ci, on envoie les termes à gauche (cela n'a pas d'importance, on aurait pu les envoyer à droite). $$\begin{align}-x^2+2x+5 &= x+3 \\ \Rightarrow\ -x^2+x+2 &= 0 \end{align}$$
   $b^2-4ac=1^2-4(-1)(2) = 9 >0,$ le système a donc deux solutions.
    

3. On peut utiliser la formule quadratique $x_{1,2} = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$ où $a=-1$, $b=1$ et $c=2.$ $$\begin{align}x_{1,2} &= \dfrac{-1 \pm \sqrt{1^2 - 4 (-1)(2)}}{2 \times 1} \\ &= \dfrac{-1 \pm \sqrt{9}}{2} \\ &= \dfrac{-1 \pm 3}{2} \\\\ x_1&= \dfrac{-1 + 3}{-2} = -1 \\ x_2 &= \dfrac{-1-3}{-2} = 2 \end{align}$$

4. On trouve les valeurs de $y$ en remplaçant $x$ dans l'une ou l'autre des deux équations de départ. $$\begin{align}y_1 &= \ x_1+3 &y_2 &= x_2+3 \\ &= -1+3 & &=\ 2\ +3 \\ &=\ 2 & &=\ 5 \end{align}$$

5. Ainsi les couples solutions du système initial sont $(-1,2)$ et $(2,5).$

Soit le système d'équations suivant : $$\begin{cases}y=-2x^2+x-2 \\y=\ 2x+1 \end{cases}$$

1. On peut écrire l'égalité suivante : $-2x^2+x-2=2x+1$

2. On envoie tous les termes du même côté de l'égalité. Dans ce cas-ci, du côté gauche. $$\begin{align} -2x^2+x-2 &= 2x+1 \\ \Rightarrow\ -2x^2-x-3 &= 0 \end{align}$$
   $b^2-4ac = (-1)^2 - 4 (-2)(-3) = -23 <0,$ il n'y a donc aucune solution à ce système.

Il n'y a donc pas de couple solution.

Soit le système d'équations suivant : $$\begin{cases}y=-2x^2+x-3 \\ y=-3x-1 \end{cases}$$

1. On peut écrire l'égalité suivante : $-2x^2+x-3=-3x-1.$

2. On envoie tous les termes du même côté de l'égalité. Dans ce cas-ci, du côté gauche. $$\begin{align} -2x^2+\ x-3 &= -3x-1 \\ \Rightarrow\ -2x^2+4x-2 &=0 \end{align}$$
   $b^2-4ac = 4^2 - 4(-2)(-2) = 0,$ il y a donc une seule solution à ce système.
    

3. On peut factoriser $-2x^2+4x-2$ et ainsi on obtient $-2(x-1)^2.$
   
   Alors, il faut résoudre $-2(x-1)^2=0.$ $$\begin{align} -2(x-1)^2 &= 0 \\ (x-1)^2 &=0 \\ x-1&= 0 \\ \Rightarrow\ x &= 1 \end{align}$$

4. On trouve la valeur de $y$ en remplaçant $x$ par $1.$ $$\begin{align} y &=-3x-1 \\ &= -3(1) -1 \\ &= -4 \end{align}$$

5. Le couple solution est $(1,-4).$