La résolution de problèmes impliquant la fonction logarithmique

Lorsque les athlètes commencent à s’entrainer, ils font habituellement rapidement des progrès. Après un certain temps, on entend souvent dire d'eux qu’ils « plafonnent ». En réalité, ils continuent de s’améliorer, mais leurs progrès sont de moins en moins notables. Pour cette raison, on peut comparer la courbe d’amélioration d’un athlète à une fonction logarithmique.

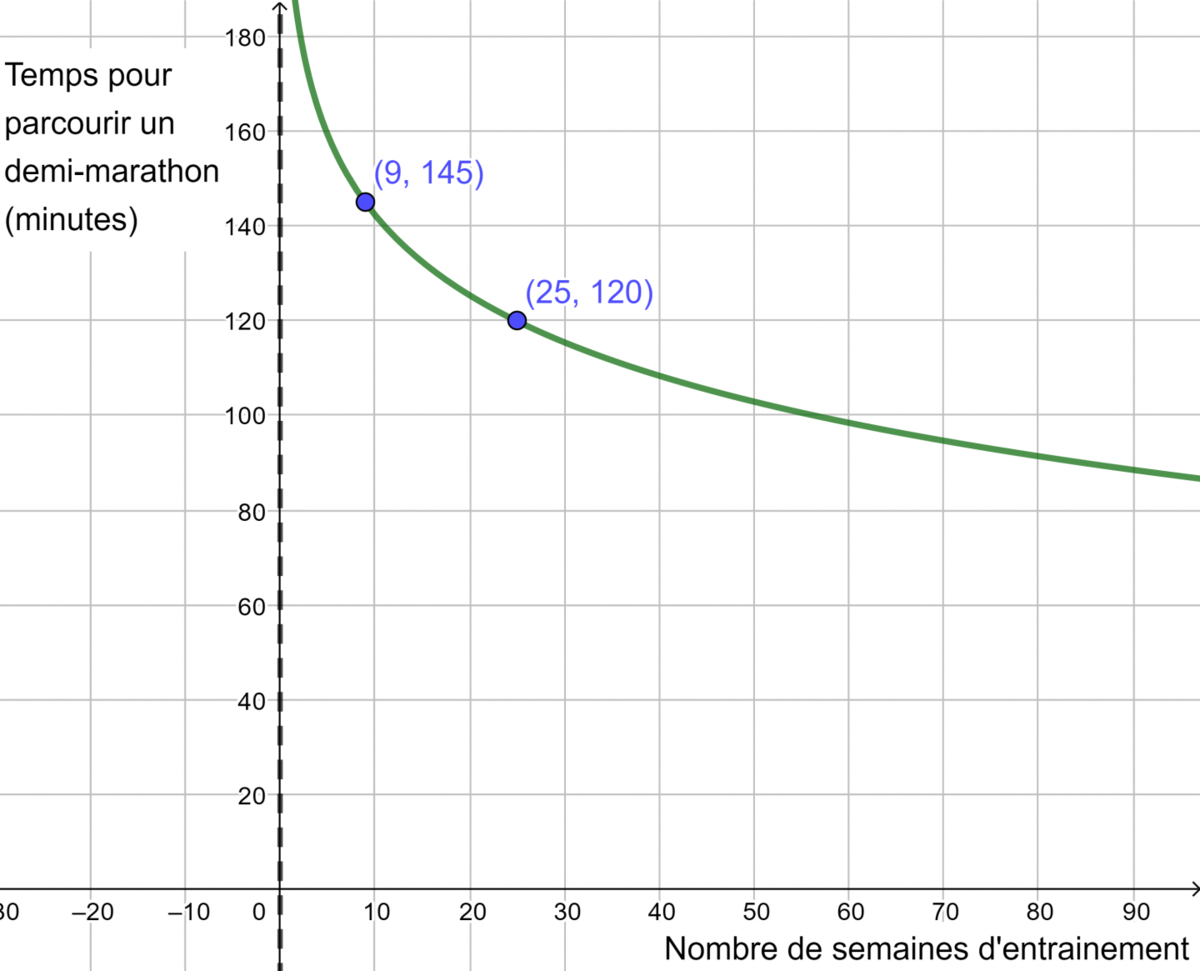
a) Quel devrait être approximativement son temps de demi-marathon après 1 année complète d’entrainement?

b) S’il continue à suivre la même tendance, après combien de semaines d’entrainement peut-il espérer faire son demi-marathon en moins de 1 h 30?

Pour répondre aux questions de l'exemple précédent, on peut utiliser la formule $f(x)=\log_c (x-h)+k$ pour trouver la règle. Voici comment faire :

1.  Remplacer $h$ par la valeur de l'asymptote

$$\begin{align} f(x) &= \log_c (x-\color{blue}{h})+k \\f(x) &= \log_c (x-\color{blue}{-0})+k \\f(x) &= \log_c x+k \\ \end{align}$$

2.  Substituer chacun des points pour créer un système d'équations

$$\begin{align} 1^{\text{er}} &\text{ couple : }(\color{green}{9},\color{red}{145}) &&2^\text{e} \text{ couple : }(\color{green}{25},\color{red}{120}) \\\\ \color{red}{f(x)} &= \log_c b\color{green}{x} && \color{red}{f(x)} = \log_c b\color{green}{x} \\\\ \color{red}{145} &= \log_c \color{green}{9}+k && \color{red}{120} = \log_c \color{green}{25}+k && \text{Substituer }\color{green}{x} \text{ et } \color{red}{y} \\\\ 145&-\log_c 9 = k && 120-\log_c 25 = k && \text{Isoler }k\end{align}$$

3.  Déterminer la valeur du paramètre $c$ à l'aide de la méthode de comparaison

$$\begin{align} k & = k \\\\ 145-\log_c9 &= 120-\log_c 25 \\\\ 25 & = \log_c 9 - \log_c25 \\\\ 25 &= \log_c \left(\dfrac{9}{25}\right) && \text{Lois des logarithmes}\\\\ c^{25} &= \dfrac{9}{25} && \text{Passer à la forme exponentielle} \\\\ \sqrt[25]{c^{25}}& = \sqrt[25]{\frac{9}{25}} && \text{Isoler c} \\\\ c & \approx 0{,}96 \end{align}$$

4.  Utiliser un des deux points fournis pour trouver la valeur du paramètre $k$

$$k = 145-\log_{0{,}96} 9 \approx 198{,}8$$

La règle est donc : $$f(x)=\log_{0{,}96}x+198{,}8$$

Cette règle est équivalente à celle qui avait été trouvée précédemment. Pour le prouver, on l'emploiera pour répondre aux questions a) et b).

a)

$$\begin{align} f(x) &= \log_{0{,}96}x + 198{,}8 \\ f(52) &= \log_{0{,}96}(52) + 198{,}8 \\ &\approx 102\ \text{minutes} \end{align}$$

En tenant compte des arrondissements, cette solution est équivalente à celle qui avait été trouvée.

b)

On a l'inéquation suivante : $$90 > \log_{0{,}96}x+198{,}8$$

On change le signe d'inégalité pour le signe d'égalité. $$90 = \log_{0{,}96}x + 198{,}8$$

On isole le logarithme. $$-108{,}8 = \log_{0{,}96}x$$

On passe à la forme exponentielle et on calcule $x.$ $$\begin{align} -108{,}8 = \log_{0{,}96}x \ \Longleftrightarrow \ 0{,}96^{-108{,}8} &= x \\ 84{,}9 &\approx x \end{align}$$

Encore une fois, après arrondissement, cette réponse est équivalente à celle qu'on avait obtenue à l'aide de l'autre formule.