La factorisation d'un nombre

La factorisation d'un nombre consiste à représenter ce nombre sous la forme d'un produit de deux facteurs ou plus.

Un facteur est un terme qui intervient dans une multiplication.

Exprime $56$ sous la forme d'un produit de facteurs.

Voici deux possibilités : $$56=2\times 28\ \text{ou}\ 56=4\times 2\times 7$$ Pour la première factorisation de $56$, les facteurs sont $2$ et $28$. Pour la deuxième, les facteurs sont $4$, $2$ et $7$.

La factorisation première consiste à écrire un nombre naturel supérieur à $1$ sous la forme d'un produit de facteurs premiers.

Un facteur premier est un facteur qui est un nombre premier.

Si on ne tient pas compte de l'ordre des facteurs, la factorisation première d'un nombre est unique.

Prenons le nombre $30$.

Il est possible de factoriser ce nombre de la façon suivante.
$$30=5\times 6$$ On remarque que le facteur $5$ est premier, mais que $6$ ne l'est pas. Pour obtenir la factorisation première de $30$, on devra factoriser le nombre $6$.
$$30=5\times \color{blue}{6}\Rightarrow 30=5\times \color{blue}{2\times 3}$$ Cette nouvelle factorisation est première, car tous les facteurs sont premiers.

La factorisation première de $30$ est donc donnée par :
$30=2\times3\times5$   (On écrit généralement les facteurs en ordre croissant)

Comme il est mentionné dans l'encadré Important ci-haut, cette factorisation est unique. Ce qui veut dire que, pour le nombre $30$, il n'existe pas d'autres factorisations premières si on ne tient pas compte de l'ordre des facteurs.
 

1. Placer le nombre à factoriser au sommet de l'arbre et le décomposer en deux facteurs que l'on inscrira au bout de deux branches.

2. Si l'un ou les deux facteurs ne sont pas premiers, continuer la factorisation jusqu'à ce que tous les facteurs aux extrémités des branches soient premiers.

3. Écrire le nombre comme un produit de facteurs premiers en utilisant les facteurs aux extrémités des branches de l'arbre.

Décompose le nombre $120$ en facteurs premiers.

1. Placer le nombre à factoriser au sommet de l'arbre et le décomposer en deux facteurs que l'on inscrira au bout de deux branches.
   
   Plusieurs factorisations sont possibles pour cette première étape. Peu importe celle qu'on choisit, on aboutira à la même factorisation première. Prenons $120=30\times4.$

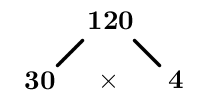
2. Si un ou les deux facteurs ne sont pas premiers, continuer la factorisation jusqu'à ce que tous les facteurs aux extrémités des branches soient premiers.
   
   On remarque que $30$ et $4$ ne sont pas premiers. On devra donc continuer la factorisation de la façon suivante.

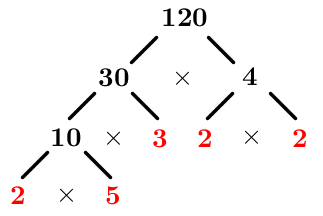
On sait qu'on a terminé lorsque tous les nombres aux extrémités des branches sont premiers.

3. Écrire le nombre comme un produit de facteurs premiers en utilisant les facteurs aux extrémités des branches de l'arbre.
   
   La factorisation première de $120$ est donc donnée par : $$120=\color{red}{2}\times\color{red}{2}\times\color{red}{2}\times\color{red}{3}\times\color{red}{5}$$

Il est possible d'utiliser la notation exponentielle pour exprimer la factorisation première d'un nombre.
En reprenant l'exemple ci-haut, on aurait $120=2^3\times 3\times 5$.

Cette forme d'écriture est parfois appelée la factorisation primaire.