La classification des polygones
Un polygone est une figure plane qui est formée par une ligne brisée fermée ayant au moins 3 côtés.
Pour travailler avec les polygones, il faut connaitre la signification de certains termes. De plus, d’autres notions connexes peuvent être consultées.
Le nom des segments
Certains des segments dans un polygone ont des noms particuliers et des caractéristiques précises. Ainsi, on peut utiliser les propriétés de ces segments pour bien définir les divers types de polygones.
La longueur et la largeur
-
La longueur |(L)| correspond à la grandeur d'un objet dans le sens de sa plus grande dimension.
-
La largeur |(l)| correspond à la grandeur d'un objet dans le sens de sa plus petite dimension.

Il est également possible de référer aux côtés du rectangle en utilisant les concepts de base et de hauteur.
La base et la hauteur
-
La base |(b| ou |B)| est un segment à partir duquel on mesure perpendiculairement une hauteur.
-
La hauteur |(h)| est la distance la plus courte entre 2 côtés parallèles ou entre un sommet et la base opposée à ce sommet.

Important!
La hauteur et la base sont toujours perpendiculaires. En d'autres mots, un angle de |90^\circ| est formé au point d'intersection de ces 2 segments (ou de leur prolongement).
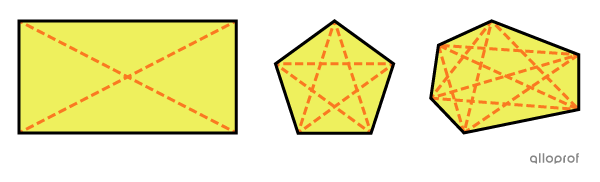
Les diagonales
Une diagonale est un segment qui relie 2 sommets non consécutifs. Ainsi, il existe plus d'une diagonale dans un même polygone.
Le nom des polygones
On nomme un polygone en fonction de son nombre de côtés, peu importe ses caractéristiques. Comme il existe une infinité de polygones différents, voici le nom de ceux qui sont les plus couramment utilisés.
|
Nombre de côtés |
Nom du polygone |
Exemples |
|---|---|---|
|
3 |
Triangle |
 |
|
4 |
Quadrilatère |
 |
|
5 |
Pentagone |
 |
|
6 |
Hexagone |
 |
|
7 |
Heptagone |
 |
|
8 |
Octogone |
 |
|
9 |
Ennéagone (nonagone) |
 |
|
10 |
Décagone |
 |
|
11 |
Hendécagone |
 |
|
12 |
Dodécagone |
 |
Il est possible de spécifier le nom des triangles et des quadrilatères selon la mesure de leurs angles, de leurs côtés ou de leurs diagonales.
Les types de polygones
Les polygones convexes
On distingue les polygones convexes des polygones non convexes selon la mesure de leurs angles intérieurs.
Un polygone est convexe si tous ses angles intérieurs ont une mesure inférieure à |180^\circ.|

Tous les polygones réguliers sont des polygones convexes.
Les polygones non convexes
Un polygone est non convexe (concave) s’il possède au moins un angle intérieur dont la mesure est supérieure à |180^\circ.|

Les polygones réguliers
Un polygone est régulier si tous ses côtés et tous ses angles intérieurs ont la même mesure.

Les polygones croisés
Un polygone croisé est un polygone dont au moins 2 côtés sont sécants.

Pour bien comprendre le polygone croisé, il faut garder en mémoire la définition même d'un polygone, soit qu'il s'agit d'une figure formée d'une ligne brisée fermée.
Les propriétés des polygones
Pour bien définir chacun des polygones, on établit généralement leurs caractéristiques selon les concepts suivants.
Les axes de symétrie
Certains polygones possèdent un ou plusieurs axes de symétrie.
Un axe de symétrie est une droite qui coupe une figure en 2 parties identiques.
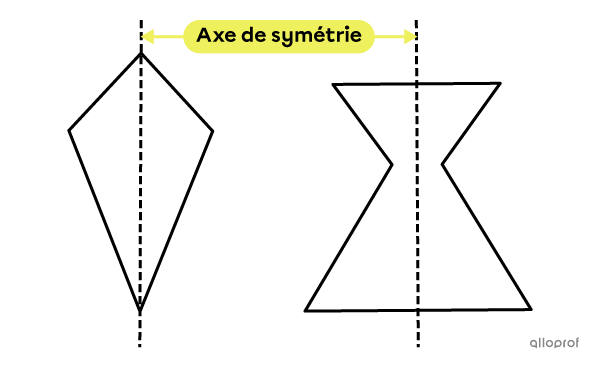
On peut associer l'axe de symétrie à l'endroit où on doit placer un miroir pour que la réflexion dans ce dernier corresponde exactement à la partie du polygone qui est cachée derrière le miroir. En d'autres mots, si on pliait un polygone en deux en suivant l'axe de symétrie, les 2 parties coïncideraient parfaitement.
Les côtés et les angles
On peut identifier un polygone selon la mesure de ses côtés et de ses angles, mais aussi grâce à la position de ceux-ci les uns par rapport aux autres.
Une paire de côtés adjacents (consécutifs) d'un polygone comprend 2 côtés qui ont un sommet en commun.
Il y a autant de paires de côtés consécutifs qu'il y a de sommets dans un polygone.
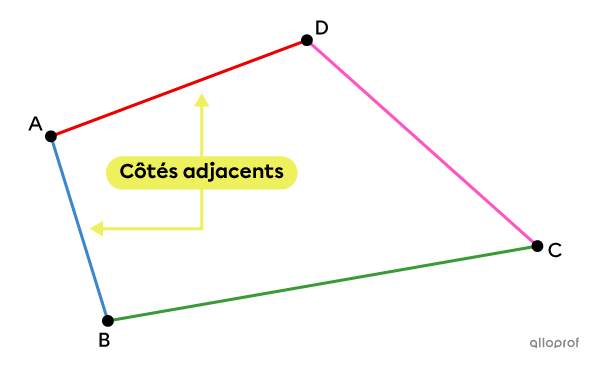
Dans ce cas, les paires de côtés adjacents sont les suivantes :
-
|\color{#ec0000}{\overline{AD}}| et |\color{#3b87cd}{\overline{AB}};|
-
|\color{#ec0000}{\overline{AD}}| et |\color{#ff55c3}{\overline{CD}};|
-
|\color{#3a9a38}{\overline{BC}}| et |\color{#3b87cd}{\overline{AB}};|
-
|\color{#3a9a38}{\overline{BC}}| et |\color{#ff55c3}{\overline{CD}}.|
On peut aussi comparer la position des angles des polygones.
Les angles consécutifs d'un polygone sont des angles qui ont un côté du polygone en commun.
On peut ainsi déduire qu'il y a autant de paires d'angles consécutifs qu'il y a de sommets dans un polygone.
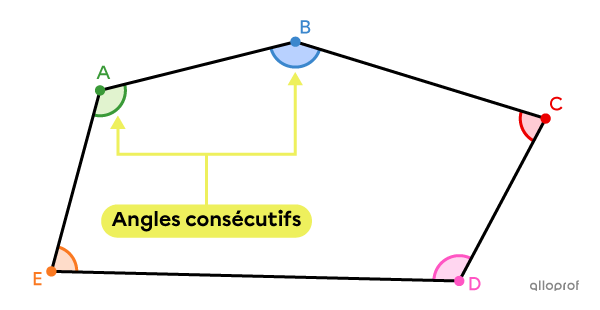
Dans le cas de ce polygone, les paires d'angles consécutifs sont les suivantes :
-
|\color{#3a9a38}{\angle{A}}| et |\color{#3b87cd}{\angle{B}};|
-
|\color{#3b87cd}{\angle{B}}| et |\color{#ec0000}{\angle{C}};|
-
|\color{#ec0000}{\angle{C}}| et |\color{#ff55c3}{\angle{D}};|
-
|\color{#ff55c3}{\angle{D}}| et |\color{#fa7921}{\angle{E}};|
-
|\color{#fa7921}{\angle{E}}| et |\color{#3a9a38}{\angle{A}}.|
En se basant sur le nombre de côtés d'un polygone, on peut établir la position relative entre 2 angles, 2 côtés, ou un angle et un côté.
La somme des angles intérieurs d'un polygone
Les 2 formules suivantes permettent de déterminer la somme des angles intérieurs d’un polygone selon son nombre de côtés. Elles sont parfaitement équivalentes.
|\begin{align}\text{Somme}\ \angle \ \text{int.} &=(n-2) \times 180\\\\ \text{Somme}\ \angle \ \text{int.} &=180n-360\end{align}|
où
|n :| nombre de côtés du polygone
|
Polygone |
|\boldsymbol{\textbf{Somme}\ \angle \ \textbf{int.}= (n-2) \times 180}| |
|---|---|
|
Triangle |
|\text{Somme}\ \angle \ \text{int.}= (3-2) \times 180=180^\circ| |
|
Quadrilatère |
|\text{Somme}\ \angle \ \text{int.}= (4-2) \times 180=360^\circ| |
|
Pentagone |
|\text{Somme}\ \angle \ \text{int.}= (5-2) \times 180=540^\circ| |
|
Hexagone |
|\text{Somme}\ \angle \ \text{int.}= (6-2) \times 180=720^\circ| |
|
Heptagone |
|\text{Somme}\ \angle \ \text{int.}= (7-2) \times 180=900^\circ| |
|
Octogone |
|\text{Somme}\ \angle \ \text{int.}= (8-2) \times 180=1\ 080^\circ| |
|
Ennéagone |
|\text{Somme}\ \angle \ \text{int.}= (9-2) \times 180=1\ 260^\circ| |
|
Décagone |
|\text{Somme}\ \angle \ \text{int.}= (10-2) \times 180=1\ 440^\circ| |
|
Hendécagone |
|\text{Somme}\ \angle \ \text{int.}= (11-2) \times 180=1\ 620^\circ| |
|
Dodécagone |
|\text{Somme}\ \angle \ \text{int.}= (12-2) \times 180=1\ 800^\circ| |
Exercice
- Haut de page
- Le nom des segments
- La longueur et la largeur
- La base et la hauteur
- Les diagonales
- Le nom des polygones
- Les types de polygones
- Les polygones convexes
- Les polygones non convexes
- Les polygones réguliers
- Les polygones croisés
- Les propriétés des polygones
- Les axes de symétrie
- Les côtés et les angles
- Définition
- La somme des angles intérieurs d'un polygone
- Exercice

















































