Memory Aid | Mathematics — Secondary 4 (CST)
Here is a brief study guide containing all the concepts covered in the Secondary 4 CST mathematics pathway. To explain everything, each formula will be followed by an example and a link to a concept sheet in our virtual library.
Arithmetic and Algebra
- First-Degree Polynomial Function (Function Form)
- Second-Degree Polynomial Function
- Exponential Function
- Step Function (Greatest Integer Function)
- The Periodic Function
- Studying Functions and their Properties
- Solving a System of Equations Using Comparison
- Solving a System of Equations Using Substitution
- Solving a System of Equations Using Elimination
Arithmetic and Algebra
First-Degree Polynomial Function (Functional Form)
y=ax+by=ax+b
where
a=ΔyΔx=y2−y1x2−x1a=ΔyΔx=y2−y1x2−x1
With the information provided in the graph below, determine the line’s equation in function (standard) form.
See solution
Second-Degree Polynomial Function
y=ax2y=ax2where the value of aa is determined by substituting a known point.
With the information provided in the graph below, determine the equation of the parabola.
See solution
Be careful!
For a second-degree polynomial function, a≠ΔyΔx.a≠ΔyΔx.
Exponential Function
y=a(c)xy=a(c)x where
aa: Initial value
cc: Base (multiplying factor)
In 2005, there were 500 toads in a pond. The population is decreasing by 5% each year. If the population continues to decline at this pace, in what year will there be approximately 368 toads?
See solution
Step Function (Greatest Integer Function)
In this type of graph, the solid (closed) points (∙∙) represent datas that are included, while empty (open) points (∘∘) represent datas that are not included.
When the Videotron Centre opened in the city of Quebec, all Quebecers could purchase tickets to visit. In theory, the visit lasted two hours, but visitors had the option of leaving after one hour. This situation can be modelled according to the following graph:
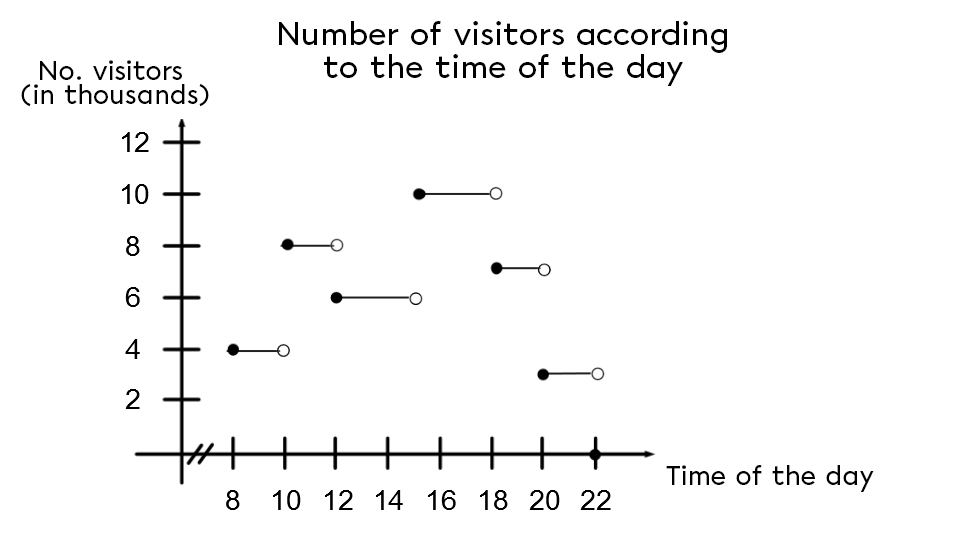
According to the graph above, how many Quebecers were visiting the Videotron Centre at 6 p.m.?
See solution
The Periodic Function
In a periodic function, a cycle is a repeating pattern, while the period is the length of one cycle along the xx-axis.
Marie-Claude decides to get back in shape after a vacation by cycling with her group of friends. A coach travels with the group, guiding them and deciding what speed to maintain. The trainer gives the following graph to each group member to prepare them for the next session:
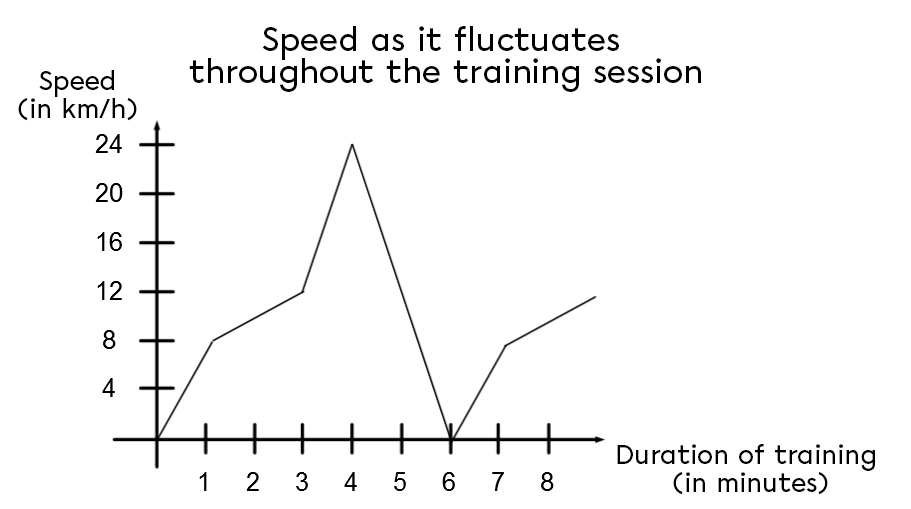
The training consists of repeating the same route for 45 minutes. By the end of her training, how many minutes, in total, will Marie-Claude have pedaled at a minimum speed of 16 km/h?
See solution
See also
Studying Functions and their Properties
The same properties must be analyzed each time a function is studied:
-
the domain: all possible xx values
-
the range: all possible yy values
-
the x-intercept: the value of xx when y=0y=0
-
the y-intercept: the value of yy when x=0x=0
-
maximum: the greatest value of yy
-
minimum: the smallest value of yy
-
increase: when the graph "goes upwards" or is constant
-
decrease: when the graph "goes downwards" or is constant
-
positive sign: interval of x of the graph that is above or equal to the xx-axis
-
negative sign: interval of x of the graph that is below or equal to the xx-axis
As an accountant of a large company, you must give a detailed account of the trends in profits over the past year. To help, here is a graph of the last 12 months.

To properly defend your argument, you must complete a full study of the graph before preparing your presentation speech.
See solution
See also
Solving a System of Equations Using Comparison
Follow these steps to solve a system of equations using comparison:
-
Identify the variables associated with the unknowns.
-
Create the equations according to the situation.
-
Isolate the same variable in each equation.
-
Compare the two equations to form a new one.
-
Solve this new equation.
-
Substitute the found variable’s value into one of the starting equations to find the value of the other.
At a corner store, a group of workers buys 4 coffees and 6 muffins for $15.06. $15.06. The next day, this same group buys 3 coffees and 5 muffins for $11.97. $11.97. If the following day they want to buy 6 coffees and 4 muffins, how much will it cost?
See solution
See also
Solving a System of Equations Using Substitution
We can follow these steps to solve a system of equations using substitution:
-
Identify the variables associated with the unknowns.
-
Create the equations according to the situation.
-
Isolate a variable in one of the two equations.
-
Substitute this same variable in the other equation with the algebraic expression associated with it.
-
Solve this new equation.
-
Substitute the found variable’s value into one of the starting equations to find the value of the other variable.
At a corner store, a group of workers buys 4 coffees and 6 muffins for $15.06. $15.06. The next day, this same group buys 3 coffees and 5 muffins for $11.97. $11.97. How much will it cost if they want to buy 6 coffees and 4 muffins the day after that?
See solution
See also
Solving a System of Equations Using Elimination
We can follow these steps to solve a system of equations through elimination:
-
Identify the variables associated with the unknowns.
-
Create the equations according to the situation.
-
Find equivalent equations to obtain the same coefficient for the same variable.
-
Subtract the two equations.
-
Isolate the remaining variable to find its value.
-
Substitute the found value of this variable into one of the starting equations to find the value of the other variable.
At a corner store, a group of workers buys 4 coffees and 6 muffins for $15.06. $15.06. The next day, the same group buys 3 coffees and 5 muffins for $11.97. $11.97. How much will it cost if they want to buy 6 coffees and 4 muffins the day after that?
See solution
See also
Geometry
Metric Relations in Right Triangles
We can deduce three theorems from the following right-angled triangle.
-
The measure of each side of the right angle in a right triangle is the geometric mean between its projection onto the hypotenuse and the hypotenuse itself. ma=ac ⇔ a2=mcnb=bc ⇔ b2=nc
-
In a right triangle, the measure of the height from the vertex of the right angle (altitude) is the geometric mean of the projections of the sides onto the hypotenuse. mh=hn ⇔ h2=mn
-
The product of the measures of the hypotenuse and the height (altitude) in a right triangle equals the product of the measures of the sides of the right angle. ch=ab
To stand out from other contractors, a construction company suggests houses with roofs of different shapes. The following form is among these choices:
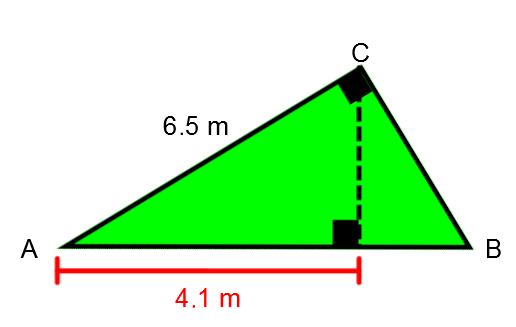
An entrepreneur needs the two missing outer measurements of this triangle (¯AB,¯BC) to estimate production costs. Help him find them.
See solution
See also
Trigonometric Relations in Right-Angle Triangles
Considering the angle θ as a reference, we get:
sinθ=Measure of the side opposite to θMeasure of the hypotenuse
cosθ=Measure of the side adjacent to θMeasure of the hypotenuse
tanθ=Measure of the side opposite to θMeasure of the side adjacent to θ
Finding a Missing Side Measurement
The elevation angle of a house's roof trusses must be a minimum of 25∘ for building standards to be met. To ensure this constraint is respected, a manufacturer decides to make this angle 35∘. If we know that the length of the roof truss is 13 metres, what will be the measurements of the other two sides?
See solution
Finding the Measure of a Missing Angle
To determine a helicopter’s route to rescue people in distress in the forest, a map of the region has been triangulated with the current location of the helicopter, the hospital, and the people who need help.
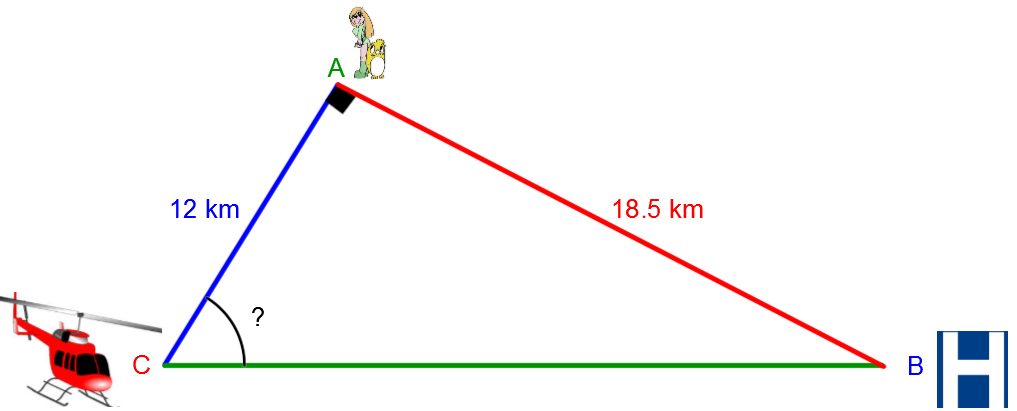
According to this drawing, what angle of orientation should the helicopter use to reach the people in distress as quickly as possible?
See solution
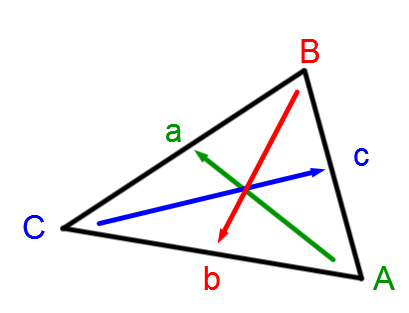
The Law of Sines
It is possible to deduce a series of equivalences for any given triangle.
asinA=bsinB=csinC
Finding a Missing Side Measurement
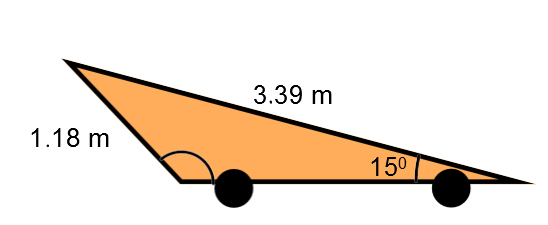
At some Western events, horse races are organized to liven up the show. During these races, cowboys must ride around each of three barrels, which are arranged in the shape of an isosceles triangle.
With the measurements given, what is the distance between each barrel?
See solution
To maximize aerodynamics, the shape of some race cars resembles a triangle.
What should the measurement of the angle near the rear wheel be to maintain these proportions?
See solution
Be careful!
When identifying the triangle, it is essential to identify:
-
side a opposite to angle A
-
side b opposite to angle B
-
side c opposite to angle C
See also
Heron's Formula
We can calculate the area of any triangle using the formula below.
Area=√p(p−a)(p−b)(p−c)
where
p=a+b+c2
To ensure its security, a bank wants to calculate the area of its floor that is covered by surveillance camera.
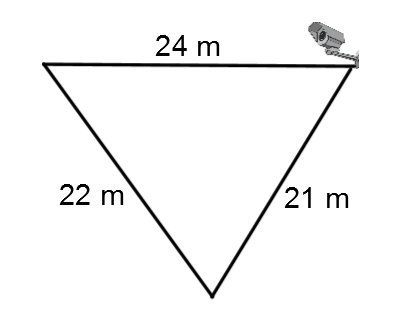
Determine the area of this space using the information provided above.
See solution
Minimum Conditions for Isometric Triangles
-
A - S - A: Two triangles are isometric when a pair of corresponding congruent sides is located between two pairs of corresponding congruent angles.
-
S - A - S: Two triangles are isometric when a pair of corresponding congruent angles is located between two pairs of corresponding congruent sides.
-
S - S - S: Two triangles are isometric when all pairs of corresponding sides are congruent.
Due to machinery problems, employees at a construction company must assemble the triangular-shaped roof trusses themselves to complete the construction of a house. However, they must make sure that all of the trusses are identical.
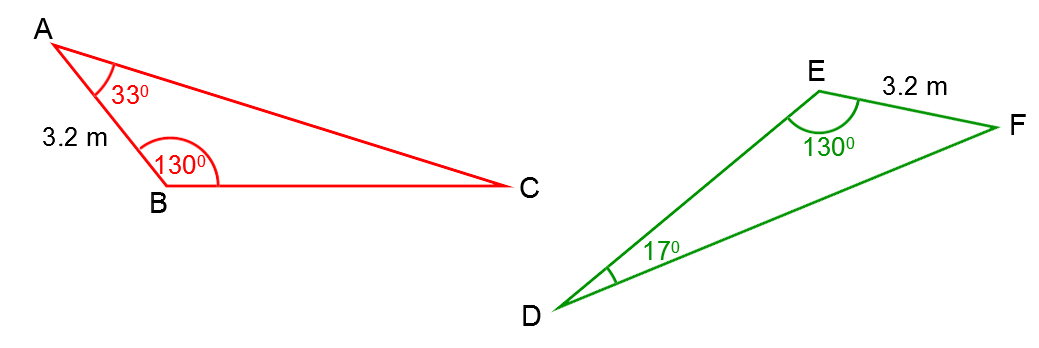
Using the information provided above, demonstrate that these two constructions are congruent.
See solution
Minimum Conditions for Similar Triangles
-
A - A: Two triangles are similar when two pairs of corresponding angles are congruent.
-
S - A - S: Two triangles are similar when a pair of corresponding congruent angles is located between two pairs of proportional corresponding sides.
-
S - S - S: Two triangles are similar if all three pairs of corresponding sides are proportional.
The city is organizing a family run as part of a fundraiser for a community group. They want the path taken by the adults to be similar to the one taken by the children.
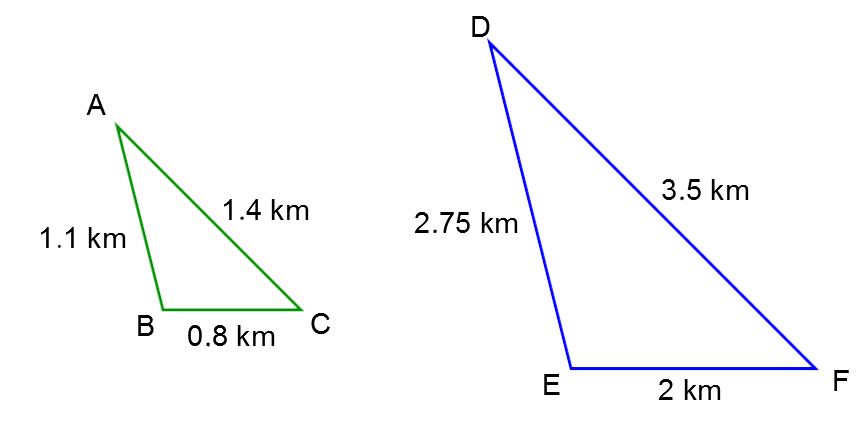
Demonstrate that the two paths are similar using the information provided above.
See solution
Analytic Geometry
The Distance Between Two Points
Distance=√(y2−y1)2+(x2−x1)2
where
(x1,y1): Coordinates of the starting point of the segment
(x2,y2): Coordinates of the ending point of the segment
To determine the amount of gasoline that an airplane must have in its tank to complete a Montreal-Paris flight, both cities are represented on a Cartesian plane (graduated in kilometres).
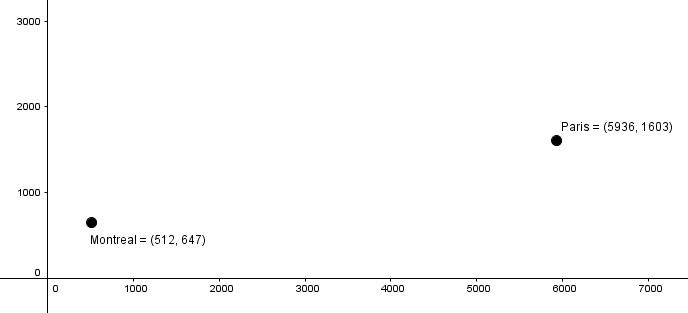
What is the distance, in kilometres, between these two cities?
See solution
See also
The Coordinates of a Division Point
Consider (x,y), the coordinates of the desired division point. x=x1+ab(x2−x1) y=y1+ab(y2−y1)
Where
(x1,y1): Starting point of the segment
(x2,y2): Endpoint of the segment
ab: Fraction that defines the division of the segment (part to whole)
Every morning, you wait at the bus stop for the bus to take you to school. You’ve noticed that, to centralize the stop for the students in the area, the segment of the street from your house to the school has been divided into a ratio of 1:4.
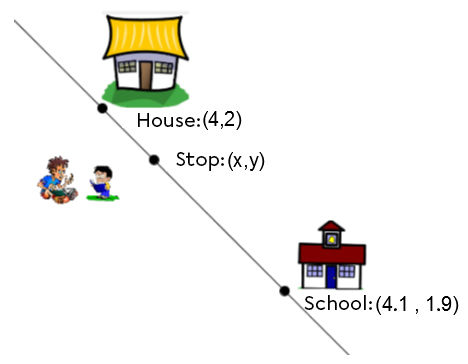
Using the given information, determine your bus stop’s coordinates.
See solution
Be careful!
It is important to differentiate between the two types of notations that are used to illustrate the portions associated with a division point in order to use the appropriate notation for the formula: Ratioa:b⇔ Fractionaa+b
Parallel Lines
The lines y1=a1x+b1 and y2=a2x+b2 are parallel if and only if a1=a2.
What is the equation of the line that is parallel to the one identified in the Cartesian plane below and that passes through point C?
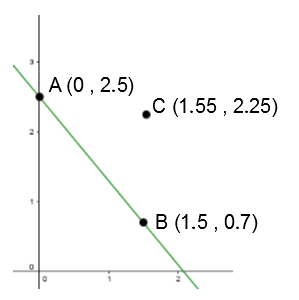
See solution
Perpendicular Lines
The lines y1=a1x+b1 and y2=a2x+b2 are perpendicular if and only if a1×a2=−1.
We also say that two lines are perpendicular if the slope of one is the opposite of the reciprocal of the slope of the other: a2=−1a1.
What is the equation of the line that is perpendicular to the one identified in the Cartesian plane below and that passes through point C?
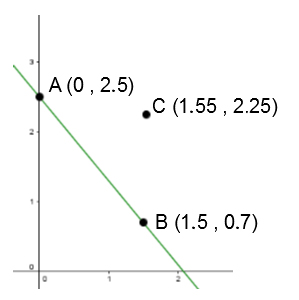
See solution
Statistics
Mean Deviation
MD=∑∣xi−¯x∣n
Where
xi represents each data.
∑ represents the sum.
n represents the total number of data.
During the last month, 11 houses in the same neighbourhood were sold for the following prices:
$156 700, $158 900, $159 000 $162 500 $164 100, $167 400, $172 000, $175 000, $178 100, $179 000, $183 000.
For statistical purposes for realtors, calculate the mean deviation of this distribution.
See solution
See also
The Percentile Rank of a Data Value and the Stem-and-Leaf Plot
R100(x)=number of data less than the value in question+number of equal data 2total number of data×100
Note: We round up to the whole number if the answer is not a whole number.
Candidates must pass a written test before being hired to fill positions in the federal government’s public sector. Here is the list of results, in percentages, of the different candidates:
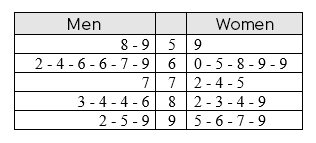
To ensure that they retain the best candidates, only those with a result higher than the 85th percentile rank will be retained. In light of this information, will your application be successful if you get a result of 84 %?
See solution
Finding a Data Value From a Percentile Rank
Position of the data =percentile rank100×total number of data
Note: Round down if the answer is not a whole number.
Candidates must complete a written test before being hired to fill positions in the federal public sector. Here is the list of results, in percentages, of the different candidates:
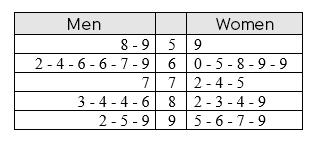
To ensure that you keep the best candidates, only those with a result higher than the 82nd percentile rank will be retained. In light of this information, starting from which test result will the candidates be selected?
See solution
Scatter Plots
The scatter plot is used to estimate the correlation between two variables. The correlation coefficient must be calculated to get a more precise idea of the correlation.
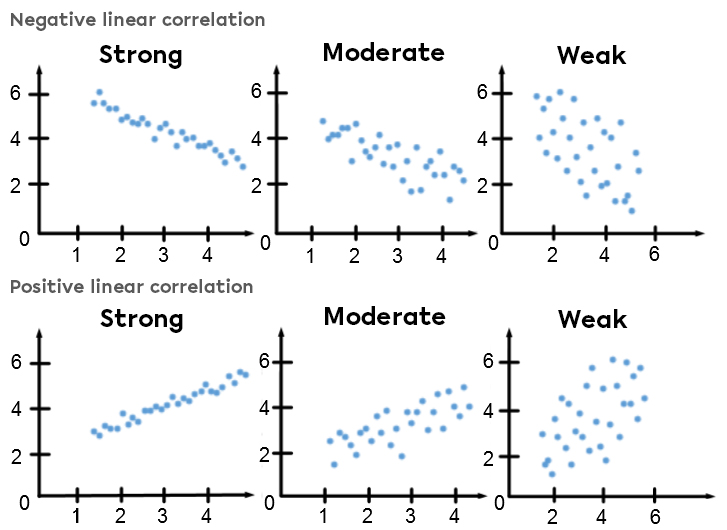
A new company has increased its profits for five years and seeks to expand its production centre. However, the owners want to ensure that the economic growth of their company is positive and strongly correlated. To break it all down, here's a count of business income for the past 30 weeks.
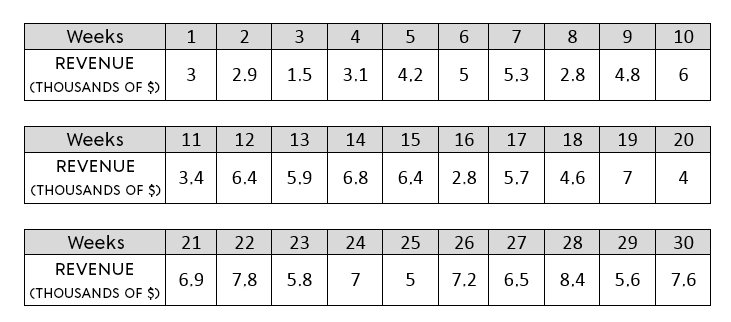
In your opinion, is the economic growth of the company positive and strongly correlated?
See solution
See also
The Correlation Coefficient
After framing the scatter plot and measuring the length (L) and width (l) of the rectangle:
r=±(1−lL) The sign depends on the direction of the scatter plot (whether it is increasing or decreasing).
This coefficient can also be used to qualify the correlation:
| Value r | Linear correlation strength |
|---|---|
| Near 0 | >Zero |
| Near ±0.50 | Weak |
| Near ±0.75 | Moderate |
| >Near ±0.87 | Strong |
| Near ±1 | Very strong |
| ±1 | Perfect |
To take stock of the success of students who enroll in adult education institutions, the administration team is studying the correlation between absenteeism (in hours) and students’ final grades (in %). They grouped the data into a scatter plot to properly analyze the situation:
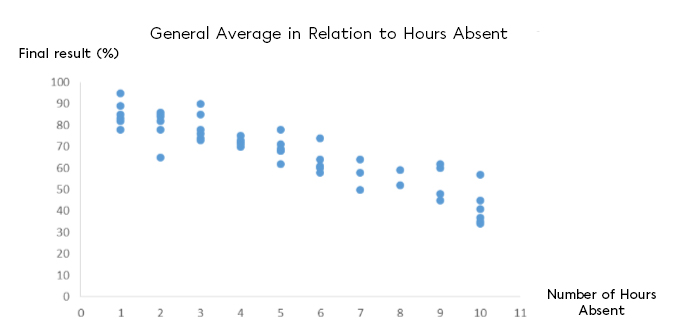
What is the correlation coefficient of this study?
See solution
See also
The Regression Line (Median-Median)
Follow these steps to find the equation of the regression line according to the Median-Median method:
-
Put the points in ascending order according to the value of x.
-
Divide the pairs into three equal groups, if possible.
-
Calculate the median coordinates (M1,M2,M3) of each group.
-
Calculate the mean coordinates (P1) of the three midpoints.
-
Calculate the value of the slope (a) with M1 and M3.
-
Calculate the value of the initial value (b) using P1.
-
Write the equation of the regression line in the form y=ax+b.
Before building a new condo tower and doing the landscaping, the heights of the surrounding trees are measured to ensure they do not obscure the view for at least the next 20 years. To estimate the height the balconies should be, the following table of values is used:

Using this information, determine how high the first balconies should be so that their view is not obstructed by trees.
See solution
Be careful!
Even though the situation and data are the same, it is normal that the final answer varies depending on the method used (Median-Median method or Mayer method).
Since these methods are used to estimate and not to predict outcomes with certainty, there may be a difference between the two outcomes.
The Regression Line (Mayer)
Follow these steps to find the equation of the regression line according to Mayer’s method:
-
Put the points in ascending order according to the value of x.
-
If possible, divide the pairs into two equal groups.
-
Calculate the mean points (P1 and P2) of each group.
-
Use these mean points to find the value of the slope (a) and the initial value (b).
-
Write the equation of the regression line in the form y=ax+b.
Before building a new condo tower and doing the landscaping, the heights of the surrounding trees are measured to ensure they do not obscure the view for at least the next 20 years. To estimate the height that the balconies should be, the following table of values is used:

Using this information, determine how high the first balconies should be so that the view is not obstructed by trees.
See solution
Be careful!
Although the situation and data are the same, it is normal that the final answer varies depending on the method used (Median-Median method or Mayer method).
Since these methods are used to estimate and not to predict outcomes with certainty, there may be a difference between the two outcomes.
See also
- Top of page
- Arithmetic and Algebra
- First-Degree Polynomial Function (Functional Form)
- Second-Degree Polynomial Function
- Exponential Function
- Step Function (Greatest Integer Function)
- The Periodic Function
- Studying Functions and their Properties
- Solving a System of Equations Using Comparison
- Solving a System of Equations Using Substitution
- Solving a System of Equations Using Elimination
- Geometry
- Metric Relations in Right Triangles
- Trigonometric Relations in Right-Angle Triangles
- The Law of Sines
- Heron's Formula
- Minimum Conditions for Isometric Triangles
- Minimum Conditions for Similar Triangles
- Analytic Geometry
- The Distance Between Two Points
- The Coordinates of a Division Point
- Parallel Lines
- Perpendicular Lines
- Statistics
- Mean Deviation
- The Percentile Rank of a Data Value and the Stem-and-Leaf Plot
- Finding a Data Value From a Percentile Rank
- Scatter Plots
- The Correlation Coefficient
- The Regression Line (Median-Median)
- The Regression Line (Mayer)
