The Exponential Function
The family of exponential functions includes all functions for which the independent variable |\boldsymbol{(x)}| is an exponent.
All exponential functions have an asymptote. Graphically, this means that exponential functions are represented by a curve that approaches a horizontal line without ever intersecting it.
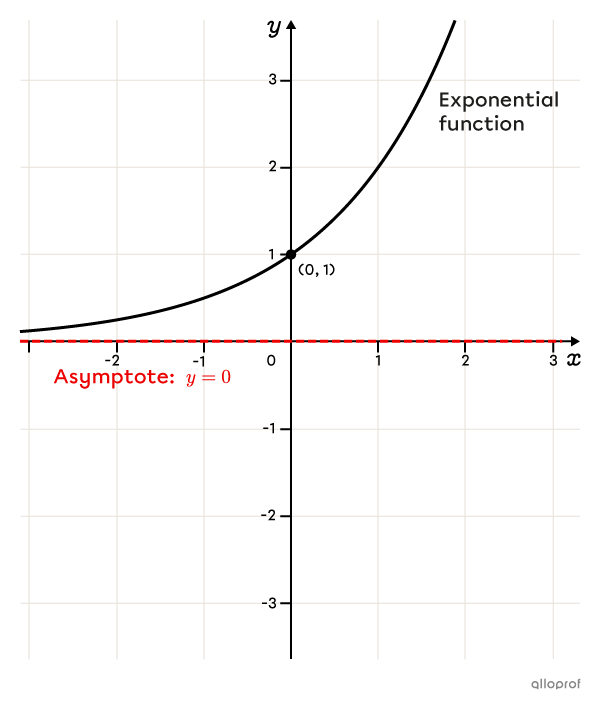
Exponential functions can be represented in one of the following forms.
Basic form||f(x)=c^x||
Simplified standard form||f(x)=a(c)^x||or||f(x)=a(c)^{bx}||
Standard form||f(x)=a(c)^{b(x-h)}+k||
Be careful!
The base |(c)| of an exponential function is always a number that is greater than |0| and not equal to |1.|
The Exponential Function in Simplified Standard Form (Secondary 4)
The exponential function is generally given in one of the 2 following forms.
||f(x)=a(c)^x||
||f(x)=a(c)^{bx}||
Important!
A simplified exponential function always has the following characteristics:
-
One asymptote whose rule is |y=0|
-
No x-intercept (zero)
-
One y-intercept with coordinates |(0,a)|
In the following interactive animation, you can move the cursors to observe the roles of parameters |a,| |b| and |c.|
The Exponential Function in Standard Form (Secondary 5)
The standard form of an exponential function is as follows:
||f(x)=a(c)^{b(x-h)}+k||
Important!
A standard exponential function always has the following characteristics:
-
One asymptote whose rule is |y=k|
-
One x-intercept (zero) if |k\ne0|
-
One y-intercept
In the following interactive animation, you can move the cursors to observe the roles of parameters |a,| |b,| |c,| |h| and |k.|