Expressing a Fraction as a Periodic Number and Vice Versa

When a group of numbers written in decimal notation repeat indefinitely, it is called a period. When the numbers are written, identify the first period after the decimal point by drawing a horizontal bar above it.

Here are some examples of periods.
$$\begin{align}0.666666666...&=0.\overline{6}\\ 0.345252525...&=0.34\overline{52}\\ 3.636363636...&=3.\overline{63}\\ 0.714285714...&=0.\overline{714285}\end{align}$$

1. Divide the numerator by the denominator.

2. Determine the period.

3. Write the number in decimal notation using the horizontal bar above the period.

Express the fraction $\displaystyle\frac{5}{6}$ in decimal notation.

1. Divide the numerator by the denominator.

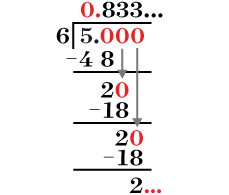
Notice that the $3$ repeats itself indefinitely.

2. Determine the period.
   $$0.8\underbrace{\color{blue}{3}}_{\color{blue}{\text{period}}}33...$$

3. Write the number in decimal notation using the horizontal bar above the period.
   
   Thus, we get $\displaystyle \frac{5}{6}=0.8\overline{3}$

Express the fraction $\displaystyle \frac{19}{11}$ in decimal notation.

1. Divide the numerator by the denominator.

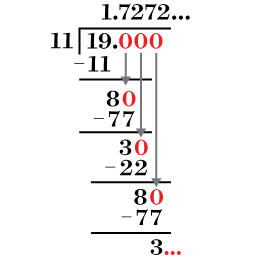
Notice that the $72$ repeats indefinitely.

2. Determine the period.
   $$1,\underbrace{\color{blue}{72}}_{\color{blue}{\text{period}}}72...$$

3. Write the number in decimal notation using the horizontal line above the period.
   
   Thus, we get $\displaystyle \frac{19}{11}=1.\overline{72}$

1. Define the periodic number as a variable. Multiply the number by the power of $10$ that places the decimal immediately before the first period (or repeating part), if necessary.

2. Multiply the number by the power of $10$ that places the decimal immediately before the first period (or repeating part).

3. Subtract the number from step 1 from the number from step 2 to obtain an integer or whole number.

4. Isolate the variable and simplify the fraction.

Express $0.\overline{36}$ in fractional notation.

1. Define the periodic number as a variable. Multiply the number by the power of $10$ that places the decimal immediately before the first period (or repeating part), if necessary. $$n=0.\overline{36}$$ Since the period is already located to the right of the decimal point, we go directly to step 2.

2. Multiply the number by the power of $10$ that places the decimal immediately after the first period (or repeating part). $$\begin{align}n\times 100&=0.\overline{36}\times 100\\ 100n&=36.\overline{36}\end{align}$$

3. Subtract the number from step 1 from the number from step 2 to obtain an integer or whole number. $$\begin{align}100n-\color{red}{n}&=36.\overline{36}-\color{red}{0.\overline{36}} & &(\text{The decimal part cancels out.})\\ 99n&=36\end{align}$$

4. Isolate the variable and simplify the fraction. $$\begin{align}99n=36\Rightarrow n&=\frac{36}{99}\\ n&=\frac{4}{11}\end{align}$$

Thus, we get $\displaystyle 0.\overline{36}=\frac{4}{11}$.

Express $1.5\overline{24}$ in fractional notation.

1. Define the periodic number as a variable. Multiply the number by the power of $10$ that places the decimal immediately before the first period (or repeating part) if necessary. $$n=1.5\overline{24}$$ Note that the period is not located next to the decimal point.
   Therefore, we must multiply by $10$ to move it. $$\begin{align}n\times 10&=1.5\overline{24}\times 10\\ 10n&=15.\overline{24}\end{align}$$

2. Multiply the number by the power of $10$ that places the decimal immediately after the first period (or repeating part). $$\begin{align}n\times 1000&=1.5\overline{24}\times 1000\\ 1000n&=1524.\overline{24}\end{align}$$

3. Subtract the number from step 1 from the number from step 2 to obtain an integer or whole number. $$\begin{align}1000n-\color{red}{10n}&=1524.\overline{24}-\color{red}{15.\overline{24}} & &(\text{The decimal part cancels out.})\\ 990n&=1509\end{align}$$

4. Isolate the variable and simplify the fraction. $$\begin{align}990n=1\ 509\Rightarrow n&=\dfrac{1\ 509}{990}\\ n&=\dfrac{503}{330}\end{align}$$

Thus, we get $\displaystyle 1.5\overline{24}=\frac{503}{330}$.