Zone d’entraide

PistacheSociable3750

Allo,

Nous sommes plusieurs à ne pas comprendre cette question nous n’avons jamais résolu de fonction partie entière avec deux valeurs inconnus donc pouvez-vous nous faire le calcul et nous expliquer comment y arriver svp

J’ai vu ailleurs que vous dites de résoudre partie entière et ensuite système d’équations, mais je ne sais meme pas par où commencer pour partie entière avec deux inconnus

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

FerUpsilon5520

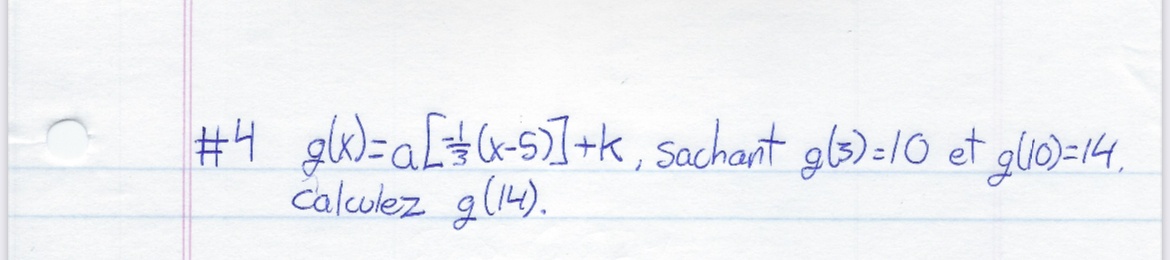
La définition de la partie entière:

"La partie entière d'un nombre, notée [x], correspond à l'unique nombre entier tel que [x]≤x<[x]+1. On appelle aussi ce symbole le plus grand entier inférieur ou égal à x."

Personnellement je trouve plus facile de me rappeler que [x} c'est le plus grand entier inférieur ou égal à x. Note qu'il faut faire attention avec les nombres négatifs.

• Pour g(3) = 10 [-(x - 5)/3] = [-(3 - 5)/3] = [2/3] = 0 donc g(3) = a.0 + k => 10 = k
• Pour g(10) = 14 [-(x - 5)/3] = [-(10 - 5)/3] = [-5/3] = -2

Je pense que tu n'auras pas de problème à résoudre le reste.

Ramzi Z

Salut !

Je comprend qu'il est difficile de visualiser la résolution de ce genre de système, mais je conseille d'y aller étape par étape. Tu peux commencer par réduire et isoler les variables dans la première équation.

https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/resoudre-une-equation-partie-entiere-m1456

$$ g(x)=a[-\frac{1}{3}(x-5)]+k $$

$$ 10=a[-\frac{1}{3}(3-5)]+k $$

\([-\frac{1}{3}(3-5)]\) devient \([\frac{2}{3}]=0\). Tu peux donc remplacer dans l'équation pour trouver la valeur de \(k\). Et puis, tu continues avec la deuxième équation pour trouver la valeur de \(a\). Pour plus de détails, tu peux visiter la fiche ci-haut.

J'espère que cela ait pu t'aider et si tu as d'autres questions, n'hésite pas !

Bonne soirée !