Zone d’entraide

CyborgSigma8168

Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.

Bonjours ,je ne comprend pas vraiment la 2e surface pourquoi il apparaît l’angle innitiale est de 39,6,j ai juste pas vraiment compris à quoi ça sers la 2e démarche,est ce que ce sera possible de m’expliquer ce problème?ps;je comprend l’angle critique c juste pas compris les démarche

merci bcp!

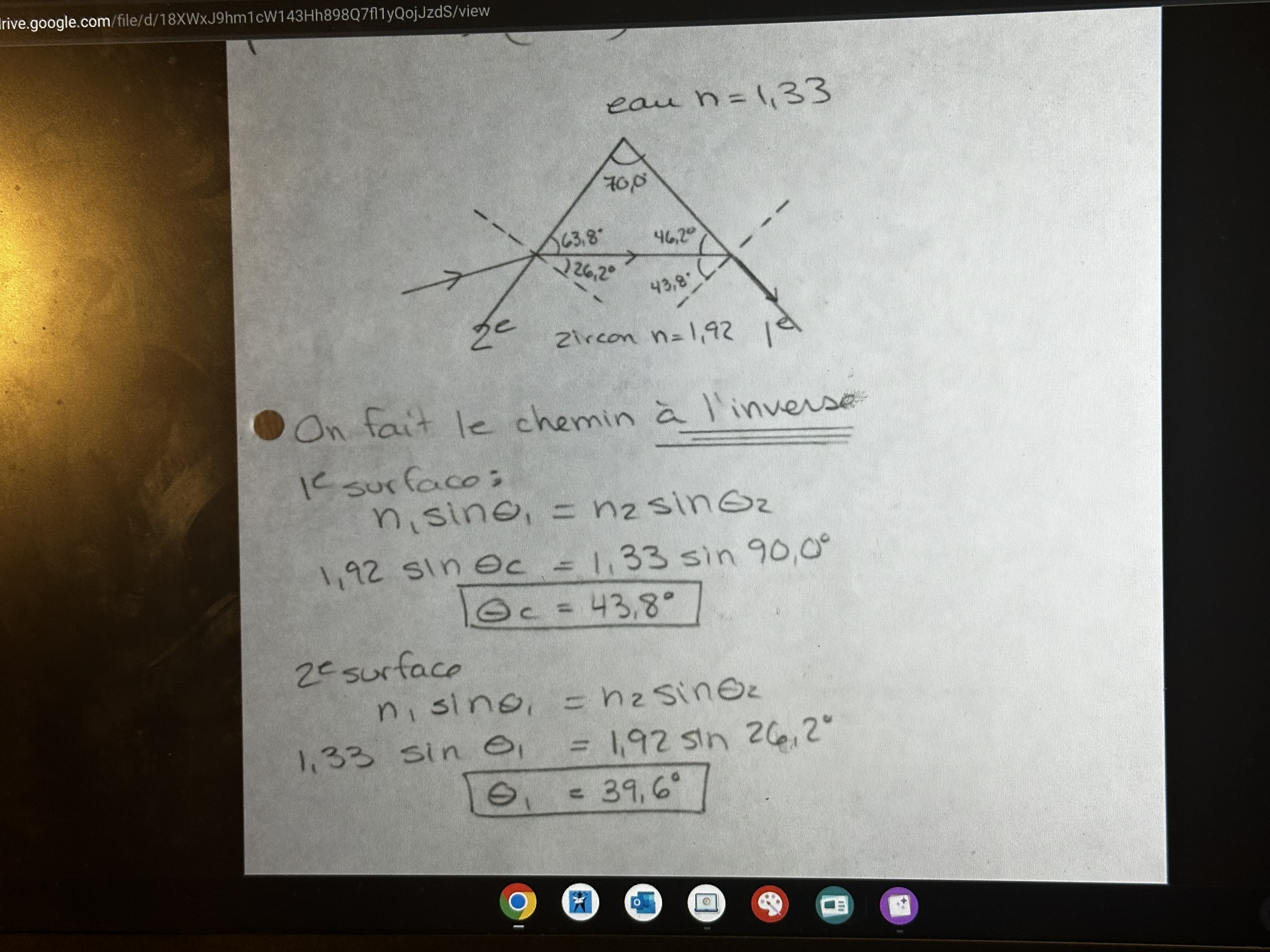
la question: Selon quel angle le rayon doit-il pénétrer dans la face gauche du prisme pour arriver à l'angle critique sur la face de droite?

GalaxieLambda6093

Salut CyborgSigma8168 ! 😊

Merci pour ta question ! 😄

Pour résoudre ce problème, on doit d’abord identifier ce qui nous manque : les deux angles, soit l’angle d’incidence (θi) et l’angle de réfraction (θr​).

Dans ton énoncé, on veut trouver l’angle d’incidence à gauche pour que l’angle final à droite soit l’angle critique (90 degrés).

Pour commencer, la loi de Snell-Descartes nous dit que :

• n1sin⁡θi=n2sin⁡θr

Ici, θr vaut 90 degrés. En remplaçant sin⁡(90) par 1, l’équation devient :

• n1sin⁡θi=n2

Tu peux donc trouver θi grâce aux indices de réfraction (n1=1,92 et n2=1,00).

Ensuite, pour comprendre d’où vient l’angle de 26,2°, il faut se rappeler que tous les angles doivent être mesurés par rapport à la normale (et non au plan). Par convention, on travaille toujours avec la normale.

Voici comment on le trouve :

• La normale forme un angle de 90 degrés avec le plan.
• Si l’angle donné par rapport au plan est de 43,8degrés, alors : 90−43,8=46,2

En travaillant avec un triangle, on utilise la somme des angles (180) pour trouver le dernier angle :

• 180−46,2−70=63,8

Enfin, pour obtenir l’angle par rapport à la normale :

• 90−63,8=26,2

On résout ce problème « à l’envers » en utilisant une propriété simple des multiplications : elles sont commutatives. Par exemple :

• 1×2=2×1

C’est cette propriété qui nous permet de remonter jusqu’à l’angle d’incidence initial en partant de l’angle critique.

J’espère que ça t’aide à y voir plus clair ! Si tu as d’autres questions, n’hésite pas à nous écrire. 😄

Bonne journée ! 😊