Secondaire 5 • 27j
Bonjour,
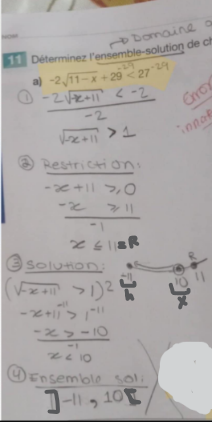
Je n'arrive pas à saisir l'ensemble solution de l'inéquation de la fonction racine carré dans ce corrigé:
Pourquoi est-ce de ]-∞ , 10[? Si nous cherchons les valeurs inférieurs, pourquoi l'ensemble solution ne commence pas par le h (soit -11), sachant que c'est la plus petite valeur possible de x???Voici mon démarche avec une petite illustration que j'avais fait:
J'ai consulté vos fiches mais je suis quand même confuse! À l'aide!







Explication d'Alloprof
Cette explication a été donnée par un membre de l'équipe d'Alloprof.
Salut!
Tout d'abord, traçons le graphique de la fonction \(f(x)=-2\sqrt{11-x}+29\) :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Le sommet (h, k) est (11, 29). Regardons pourquoi nous avons eu ce graphique.
On peut réécrire la fonction comme ceci pour avoir la forme canonique :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
$$f(x)=-2\sqrt{11-x}+29$$
$$f(x)=-2\sqrt{-x+11}+29$$
$$f(x)=-2\sqrt{-(x-11)}+29$$
Il faut absolument avoir la forme canonique pour pouvoir identifier nos paramètres a, b, h et k correctement! En effet, cela nous a permis de déterminer que le paramètre h est de 11, et non -11.
De plus, puisque le paramètre b est négatif, la branche du graphique de la fonction racine carrée est orientée vers la gauche. Donc, h est la plus grande valeur possible de x, et non la plus petite!
Voici une fiche qui pourrait t'être utile pour mieux comprendre l'effet de chaque paramètre : Le rôle des paramètres dans une fonction racine carrée | Secondaire | Alloprof
Ensuite, on cherche l'intervalle pour laquelle la fonction est inférieure à y=27 (droite horizontale mauve) :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Avec e graphique, on constate que la fonction est inférieure à 27 sur l'intervalle ]-∞, 10[, ce qui concorde avec les calculs du corrigé.
Dans tes calculs, tu as la bonne démarche, mais à la fin, tu as un nombre qui ne figure nulle part dans tes calculs (le -11), ce qui t'indique déjà que ce n'est pas la bonne réponse :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Tu dois vraiment te fier aux résultats obtenus avec tes calculs pour trouver la réponse finale. On sait que x doit être plus petit ou égal à 11 en posant la restriction (car la fonction cesse d'exister à partir de x=11, c'est-à-dire le sommet à x=h), et la solution nous dit qu'on est inférieur à y=27 si x<10. Ainsi, puisque la solution respecte la restriction, la réponse finale sera x<10, ou ]-∞, 10[.
Si on cherchait l'intervalle pour lequel la fonction est supérieure à y=27, donc on cherche l'intervalle de cette partie :
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
On peut constater à l'aide du graphique que la réponse serait ]10, 11].
À l'aide de calculs, on aurait la restriction x≤11, et la même solution, mais avec le signe inverse : x>10. Puisque la solution trouvée est affectée par la restriction, l'intervalle final serait donc x>10 et x≤11, donc ]10, 11], ce qui concorde avec ce qu'on peut observer à l'aide du graphique.
J'espère que c'est plus clair pour toi! Si tu as d'autres questions, n'hésite pas à nous réécrire! :)
Ce contenu est protégé par le droit d'auteur. Toute reproduction à l'extérieur des forums Alloprof est interdite et pourra être considérée comme une violation du droit d'auteur.
Suggestions en lien avec la question
Suggestion en lien avec la question
Voici ce qui a été trouvé automatiquement sur le site, en espérant que ça t’aide!