Subjects
Grades
Vector Components
Concept sheet | Physics
Secondary
5
To add two vectors, simply add their components. Indeed, a vector can be broken down into two components, namely, a horizontal component parallel to the x-axis and a vertical component parallel to the y-axis.
The following tool is used to determine the components of a vector.
Determining the Components of a Vector from its Magnitude and its Direction
When the vector’s magnitude and direction are known, it is possible to determine its components using trigonometric relationships.
To determine the vector’s components, use the following rules:
|| x = r \times \cos \theta |||| y = r \times \sin \theta ||
| r | represents the vector’s magnitude
| \theta | represents the vector’s direction
A vector measures |\small \text {3 u}| and it is oriented at |\small 30^{\circ}|. What are the components of the vector?
||\begin{align} x=r\times \cos \theta \quad \Rightarrow \quad
x &= 3\times \cos 30^{\circ} \\
&= 2.60 \: \text {u} \end{align}||
||\begin{align} y=r\times \sin \theta \quad \Rightarrow \quad
y &= 3\times \sin 30^{\circ} \\
&= 1.50 \: \text {u} \end{align}||
Therefore, the components of the vector are |2.60 \: \text {u}| on the x-axis (or abicissa), and |1.50 \: \text {u}| on the y-axis.
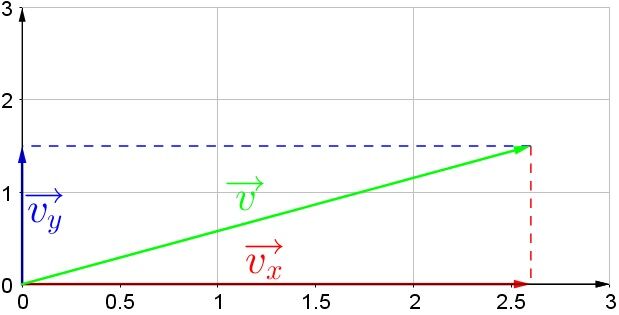
If a vector is illustrated on a Cartesian plane, the dimensions of the vector must be plotted on each of the axes to find its components.
What is the size and direction of the vector shown above?
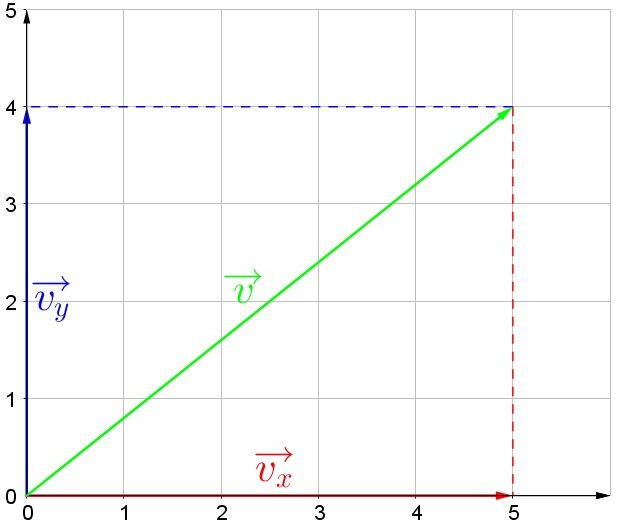
By plotting the vector on the axes (red and blue dotted lines), the vector has a horizontal component of |5 \: \text {u}| and a vertical component of |4 \: \text {u}|.
Determining the Magnitude and Direction of a Vector based on its Components
When the components of a vector are known, it is possible to determine the magnitude using the Pythagorean Theorem. To determine the angle, trigonometric ratios can be used.
To switch horizontal components | (x, y) | into a vector having a magnitude | (r) | and a direction | (\theta) |, we use the following rules:
|| r = \sqrt {x ^ 2 + y ^ 2} |||| \theta = \tan ^ {- 1} \left (\begin {array} {c} \displaystyle \frac {y} {x} \end {array} \right) ||
What is the size and direction of the vector shown above?
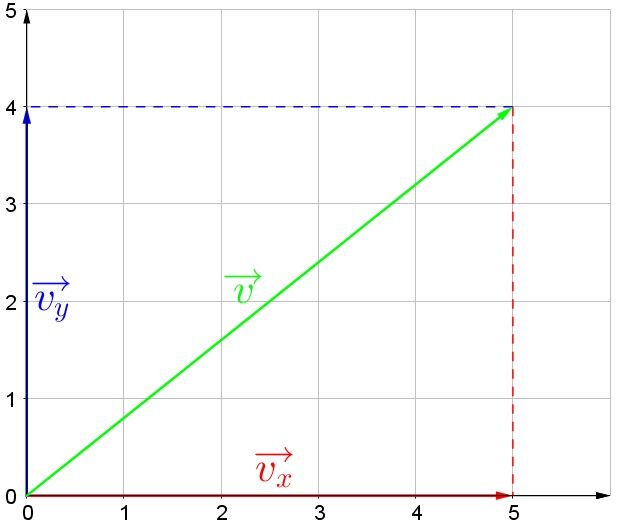
|| \begin{align} r = \sqrt{\color{red} {x}^2 + \color{blue} {y}^2} \quad \Rightarrow \quad r &= \sqrt{\color{red} {5^2} + \color{blue} {4^2}} \\ &= \sqrt{41}\\ & \approx 6.40 \: \text{u} \end{align}||
||\begin{align} \theta=\tan^{-1} \left( \frac{\color{blue} {y}}{\color{red} {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \left( \frac{\color{blue} {4}}{\color{red} {5}} \right)\\ &= \tan^{-1}\left(0.8\right)\\ & \approx 38.7^{\circ}\end{align}||
The resultant vector has a magnitude of |\text {6.40 u}| and it is located at |38.7^{\circ}| with respect to the x-axis.
To determine the value of angle |\theta|, we must determine the value of the angle between the positive x-axis (positive abscissa), which is the starting point, and the vector determined in the previous step.
