The Quadratic Function
A quadratic function is defined by a polynomial in the form of ax2+bx+cax2+bx+c, where a,b,c∈R and a≠0.
On a Cartesian plane, a quadratic polynomial function is represented by a parabola.
Be careful!
Sometimes the expression second-degree polynomial function is used as a synonym for a quadratic function. For the sake of consistency, using the expression quadratic function is preferred.
Certain terms must be defined to understand the quadratic function. Other related concepts can also be consulted.
Related Concepts
- Forms of the Equation of a Quadratic Function
- The Role of Parameters in a Quadratic Function
- Graphing a Quadratic Function
- Finding the Rule of a Quadratic Function
- The Zeroes of a Quadratic Function
- Properties of Quadratic Functions
- Solving Problems Involving Quadratic Functions
- The Inverse of Quadratic Functions
The Basic Quadratic Function
The basic function f(x)=x2 is represented by the following table of values and graph.
| x | y |
|---|---|
| −3 | 9 |
| −2 | 4 |
| −1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |

The parabolic form of the function has a vertex located at the origin (0,0) of the Cartesian plane. In addition, 2 branches of the parabola are symmetrical with respect to a vertical axis intersecting the vertex. In the case of the basic function, it is the y-axis.
The Transformed Quadratic Function
The rule of the quadratic function can be written in 4 forms.
The form centred at the origin: f(x)=ax2
The general form: f(x)=ax2+bx+c
The standard form: f(x)=a(x−h)2+k
The factored form: f(x)=a(x−x1)(x−x2)
Important!
When the independent variable of a quadratic function increases by one unit, the difference between the variations of the dependent variable is constant and equals 2a. We can use the function f(x)=2(x−1)2+1 as an example.
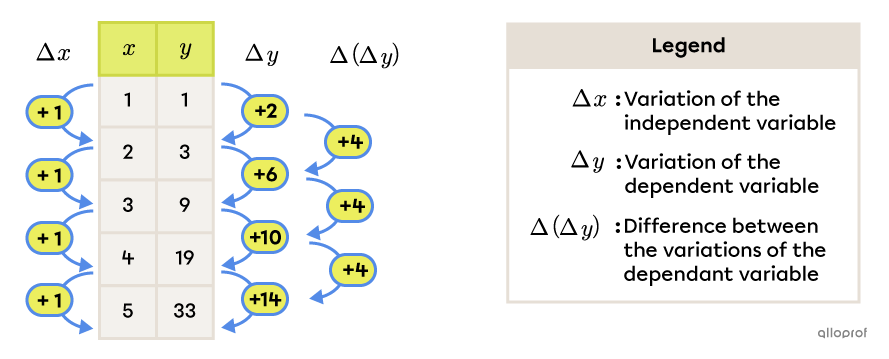
Each deviation between consecutive variations of the dependent variable is 4 or 2a. However, if 2a=4, then a=2. It is therefore the value of parameter a.
Exercise
















































