The Difference of Functions

Operations on functions are performed the same way operations on numbers are performed. Therefore, the difference of functions can be found.

• The domain of the difference function corresponds to the intersection of the domains of the functions in question. If there is a denominator, the restrictions on it must be excluded.

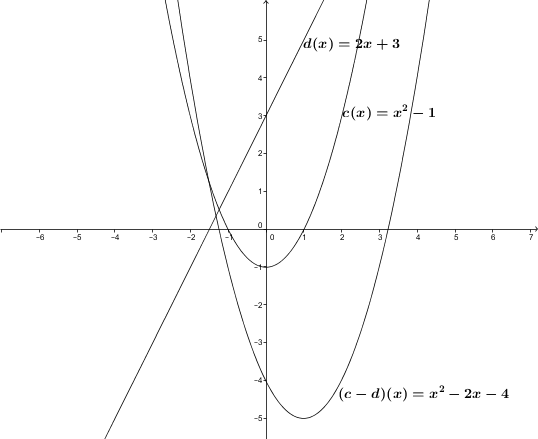
Function $c$ is defined by $c(x)=x^{2}-1$ and function $d$ is defined by $d(x)=2x+3.$ The difference in the functions will result in the following. $$\begin{align}(c-d)(x) &= c(x)-d(x) \\ &=(x^{2}-1)-(2x+3) \\ &= x^{2}-1-2x-3 \\ &=x^{2}-2x-4 \end{align}$$

The domain of function $c$ corresponds to $\mathbb{R}.$ The domain of function $d$ also corresponds to $\mathbb{R}.$ The domain of the function given by $c-d$ will correspond to the intersection of the two initial domains. Therefore, this function’s domain will be $\mathbb{R}.$

Function $p$ is defined by $p(x)=4\sin\dfrac{\pi}{10}(x)$ and function $q$ is defined by $q(x)=\dfrac{x}{5}.$ The difference in the functions will result in the following. $$\begin{align} (p-q)(x) &= p(x)-q(x) \\ &= 4\sin\dfrac{\pi}{10}(x)-\dfrac{x}{5} \end{align}$$

The domain of function $p$ corresponds to $\mathbb{R}$ and the domain of function $q$ corresponds to $\mathbb{R}.$ The domain of the function given by $p-q$ will correspond to the intersection of the two initial domains. Therefore, this function’s domain will be $\mathbb{R}.$

Function $f$ is defined by $f(x)=\dfrac{x-3}{x-4}$ and function $g$ is defined by $g(x)=\dfrac{x+2}{x^2-16}.$ The difference in the functions will result in the following. $$\begin{align} (f-g)(x) &= f(x)-g(x) \\ &= \dfrac{x-3}{x-4}-\dfrac{x+2}{x^2-16} \\ &= \dfrac{x-3}{x-4}-\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{x-3}{x-4}\times \dfrac{x+4}{x+4} -\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{(x-3)(x+4)}{(x-4)(x+4)} -\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{x^2+x-12}{(x-4)(x+4)} -\dfrac{x+2}{(x-4)(x+4)} \\ &= \dfrac{x^2+x-12-(x+2)}{(x-4)(x+4)} \\ &= \dfrac{x^2+x-12-x-2}{(x-4)(x+4)} \\ &= \dfrac{x^2-14}{x^2-16} \end{align}$$

The domain of function $f$ is $\mathbb{R} \backslash \lbrace 4 \rbrace$ and the domain of function $g$ is $\mathbb{R} \backslash \lbrace -4,4 \rbrace.$ Therefore, the domain of the resulting function is $\mathbb{R} \backslash \lbrace 4 \rbrace \cap \mathbb{R} \backslash \lbrace -4,4 \rbrace = \mathbb{R} \backslash \lbrace -4, 4 \rbrace.$

To find the difference between two functions in a graph, subtract the range of the first function by the range of the second function.

To produce the graph, make a table of values or use the peculiarities of the resulting function.

• In the first example, the table of values of the functions $c(x)=x^{2}-1,$ $d(x)=2x+3$ and $c-d,$ would result in the following.

• Since the resultant function is a quadratic function, the associated formulas can be used to find the vertex and the zeros.

Vertex:

$(c-d)(x)=x^{2}-2x-4$

$h=\dfrac{-b}{2a}=\dfrac{-(-2)}{2\times 1}=1$

$\begin{align} k &= (c-d)(h) \\ &= (c-d)(1) \\ &= (1)^{2}-2(1)-4 \\ &=-5 \end{align}$

So $(h,k)= (1,-5).$

Zeros:

$\begin{align} x_{\{1,2\}} &= \dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a} \\ &=\frac{-(-2)\pm\sqrt{(-2)^{2}-4(1)(-4)}}{2(1)} \end{align}$

We find $(-1.24, 0)$ and $(3.24, 0).$

The following graph is obtained.