Solving Problems Involving the Cosine Function
Before solving problems involving the cosine function, it is important to know how to solve a trigonometric equation or inequality and apply it in a problem with a real-world context. Here is an example inspired by physics.
The height of a mass relative to the ground can be modelled using a cosine function. This mass is attached to a spring.
Here's some information:
- The initial height of the mass is 20 cm from the ground.
- The mass takes 10 seconds to return to its initial height.
- The mass reaches a minimum height of 2 cm from the ground.
a) Determine the equation of the cosine function modelling this situation.
The equation must be found in this form: y=acos(b(x−h))+k.
Since we know the maximum height of the mass (its height), the amplitude can be calculated first.
Amplitude=max−min2=20−22=9
So, the value of a is 9. Its sign will be determined later.
Now, we can find the value of b using the period (10 seconds).
Period=2π∣b∣
Thus ∣b∣=2π10=π5.
The h parameter is 0 and the k parameter is 20−9=11.
Also, since the function decreases (the maximum height of the mass is at the beginning), then the value of a must be positive. We conclude that: a=9.
Therefore, the equation of the function can be written: y=9cos(π5x)+11.
The following graph is also obtained:
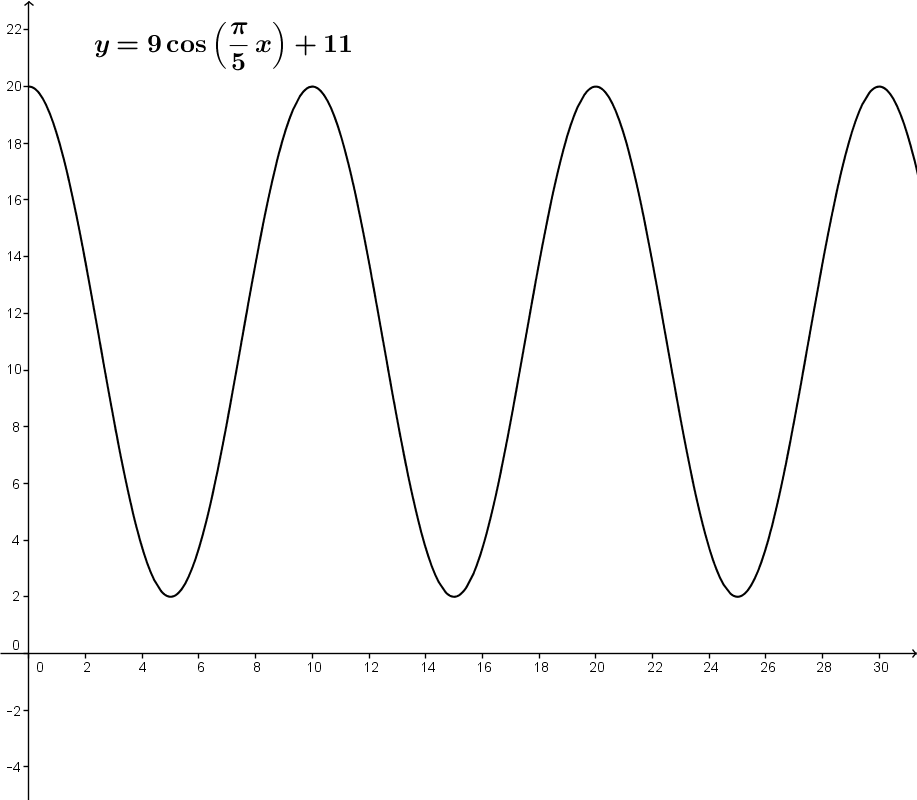
b) For a period of a minute, how long is the mass at a height greater than 12 centimetres from ground level?
First, solve the inequality at the beginning 12<9cos(π5x)+11.
Start by changing the inequality sign to the equality sign.
12=9cos(π5x)+11
1=9cos(π5x)
19=cos(π5x)
The arccosine function must be used.
This gives us the value of 1.459 radians. Next, find the other value by carrying out 2π−1.459=4.824 radians.
So, the angle must be equal to 1.459 radians or 4.824 radians. To find the values of x, π5x=1.459 and π5x=4.824 must be solved.
Solving these two equations gives us x=2.323 and x=7.678.
Next, we interpret these values.
Looking at the drawing above, we can see that the mass will have a height greater than 12 centimetres between 0 and 2.323 seconds and between 7.678 and 10 seconds.
So, the height of the mass is greater than 12 centimetres from the ground for approximately 4.645 seconds.
This is for the first cycle. In 1 minute, 6 cycles elapse (the period is 10 seconds).
We get the final answer by doing 4.645×6=27.87 seconds.
