Memory Aid | Mathematics — Secondary 5 (CST)
The following is a short preparation guide containing all the concepts covered in Secondary 5 in the CST pathway. To explain everything, each formula will be followed by an example and a link to a concept sheet in our virtual library.
Statistics: Social Choice Theory
Algebra
First Degree Linear Function (Functional and General Form)
Functional form
y=ax+b where a=ΔyΔx=y2−y1x2−x1
General form
0=Ax+By+C where A,B,C∈Z
Using the information in the table below, determine the equation for the straight line in the general form.
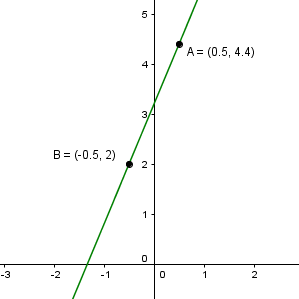
See solution
See also
Solving a System of Equations Using Comparison
Follow these steps to solve a system of equations using comparison:
-
Identify the variables associated with the unknowns.
-
Create the equations according to the scenario.
-
Isolate the same variable for each of the equations.
-
Compare the two equations to form a new one.
-
Solve this new equation.
-
Substitute the value of the found variable into one of the starting equations to find the value of the other variable.
At the corner store, workers bought 4 coffees and muffins for $15.06. The next day, the same group buys 3 coffees and muffins for $11.97. If, the next day, these workers want to buy 6 coffees and 4 muffins, how much will they have to pay?
See solution
See also
Solving a System of Equations Using Substitution
Follow these steps to solve a system of equations using substitution:
-
Identify the variables associated with the unknowns.
-
Create the equations according to the scenario.
-
Isolate a variable in one of the two equations.
-
Substitute this same variable in the other equation by the algebraic expression associated with it.
-
Solve this new equation.
-
Substitute the value of the found variable into one of the starting equations to find the value of the other variable.
At the corner store, workers bought 4 coffees and muffins for $15.06. The next day, the same group buys 3 coffees and muffins for $11.97. If, the next day, these workers want to buy 6 coffees and 4 muffins, how much will they have to pay?
See solution
See also
Solving a System of Equations Using Elimination
Follow these steps to solve an equation system using the elimination method:
-
Identify the variables associated with the unknowns.
-
Create the equations according to the scenario.
-
Find equivalent equations to obtain the same coefficient for the same variable.
-
Subtract the two equations.
-
Isolate the remaining variable to find its value.
-
Substitute the value of the found variable in one of the starting equations to find the value of the other variable.
At the corner store, workers bought 4 coffees and muffins for $15.06. The next day, the same group buys 3 coffees and muffins for $11.97. If, the next day, these workers want to buy 6 coffees and 4 muffins, how much will they have to pay?
See solution
Optimization
Generally, an optimization problem can be solved by following these steps:
-
Identify variables and unknowns.
-
Determine the equation of the function to be optimized as well as the target objective (minimize or maximize).
-
Create a system of inequalities.
-
Sketch the polygon of constraints.
-
Determine the coordinates of each of the polygon’s vertices.
-
Substitute the coordinates of each vertex in the function to be optimized to determine the optimal solution(s).
-
Give a complete answer taking into account the context.
In order to maximize his business’ profits, the owner wants to know how many jackets and shirts he must sell each week. Due to production constraints, he knows that the maximum number of shirts corresponds to the difference between 21 and quadruple the number of jackets. For transportation reasons, the number of jackets must be greater than or equal to the difference between eight and three times the number of shirts. Finally, the difference between triple the number of jackets and double the number of shirts must be at least two.
Knowing that each jacket sold brings in a profit of $32 and the profit associated with selling a shirt is $17, what is the maximum weekly profit the business owner can expect to make?
See solution
See also
Probability
Types of Events
| TYPES OF EVENTS | DEFINITION | EXAMPLE |
|---|---|---|
| Mutually exclusive | When they can't happen at the same time. | Rolling a six-sided die and getting a number that is a multiple of both 3 and 4. |
| Not mutually exclusive | When they can occur at the same time. | Drawing a random card from a 52-card deck and getting an ace that is red. |
| Dependent | When one result affects the other. | Drawing two cards successively without replacing it from a 52-card deck. |
| Independant | When one result does not affect the other. | Drawing a card from a 52-card deck and rolling a six-sided die. |
Be careful!
However, we must not forget the types of events that have been seen in class in previous years (certain, probable, impossible, elementary, complementary, compatible, and incompatible).
See also
The Odds For and the Odds Against
If a= the chances for and b= the odds against, then:
the odds (ratio) for =a:b⇒aa+b
the odds (ratio) against =b:a⇒bb+a
Thus, we obtain the net winnings according to the following proportion:
Bet amountNet gain=Number of chances on which we betTotal number of chances
Example of Chances For
In the days of the Quebec horse races, people could bet on the victories of racehorses. Each horse had odds that quantified its chances of winning. For the last race, an amateur bet $20 for victory whose odds were 1:14. So, what was the potential gain from his bet?
See solution
Example of Against Chances
In some boxing matches, you can bet on a boxer's defeat. Each boxer has odds that quantify his chances of winning. For the next fight, the champion has odds of 44:1 for his victory. So what would be the net profit of an amateur who bets $10 against a victory for the champion?
See solution
See also
Mathematical Expectation (Fair Games)
E=(p1x1+p2x2+⋯+pixi)−M
where
pi= probability of occurrence of the event i,
xi= amount associated with the event i,
M= initial bet amount
To help fund the school's freestyle ski team, the organisers are organising a fundraising event with the following prizes up for grabs.
-
one weekend family ski package ($800 value);
-
two alpine ski season tickets (value of $500 each);
-
four pairs of skis (value of $300 each);
-
eight lift tickets valid for one day (value $45 each).
Given that they have a total of 336 tickets to sell, what should be the selling price of a raffle ticket?
See solution
Important!
If E=0, the game is fair.
If E<0, the game is unfavourable to the player.
If E>0, the game is favourable to the player.
See also
Conditional Probability
P(A∣B)=P(A∩B)P(B) with P(A)>0
During the previous month, listeners to a Quebec radio station had the chance to win a trip to Walt Disney's fairytale estate. Before randomly selecting the winner, the broadcaster drew up an overall profile of the participants.

What is the probability that the winner is the father of a family with three children and that the raffle ticket was given to him as a gift?
See solution
See also
Geometry
Equivalent Figures
Important!
Two figures are equivalent when they have the same area.
To ensure that the cost of paving his new residential car park is the same as that of his old one, Julien wants his two entrances to be equivalent.
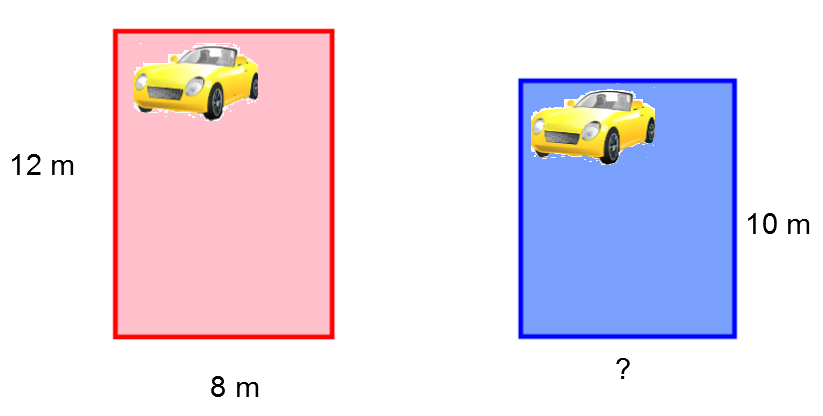
So how wide should his new parking area must be?
See solution
See also
Equivalent Solids
Important!
Two solids are equivalent when they have the same volume.
A company specialising in outdoor accessories wants to offer two different tent models. To keep production costs the same, the company wants the two models to be equivalent.
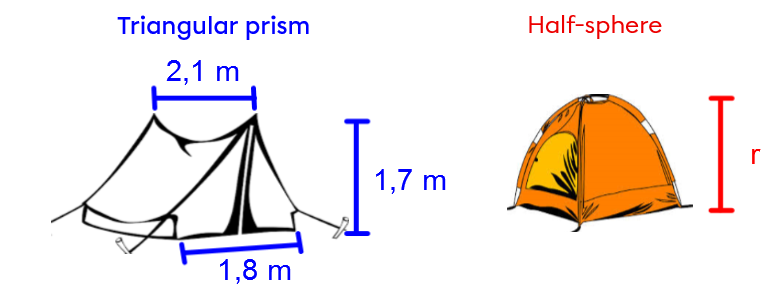
What should the height of the second model be in order to meet the similarity condition?
See solution
See also
Financial Mathematics
Properties of Exponential Notation
For all {a,b}∈R and {m,n}∈N, we deduce the following properties:
-
If am=an, then m=n.
-
am×an=am+n
-
aman=am−n where a≠0
-
(ab)m=ambm
Solve the following equation. 6 300(1.2)3x=175(7.2)2
See solution
See also
Definitions and Laws of Logarithmic Notation
For the following properties, it is important to consider {m}∈R+ and {c,n}∈R.
-
logc(1)=0
-
logc(c)=1
-
logc(mn)=nlogc(m)
-
logc(mn)=logc(m)+logc(n)
-
logc(mn)=logc(m)−logc(n)
-
logc(m)=loga(m)loga(c)
Solving an exponential equation
What is the value of x in the equation:
4500=1500(1.08)x2
45001500=15001500(1.08)x2inverse operation3=1.08x2log1.08(3)=x2definition of loglog10(3)log10(1.08)=x2change of base14.275×2≈x2×2inverse operation28.55≈x
Solving a logarithmic equation
What is the value of x in the equation:
log5(x3)+log5(x32)=log5(732)−1
log5(x3)+log5(x32)=log5(732)−13log5(x)+log5(x32)=log5(732)−1power of a log3log5(x) +(log5(x)−log5(32))=log5(732)−1log of a quotient3log5(x)+log5(x)−2.153≈4.098−1change of base law4log5(x)−2.153≈4.098−1like terms4log5(x)−2.153+2.153≈4.098−1+2.153inverse operation4log5(x)4≈5.2514inverse operationlog5(x)≈1.313⇒ 51.313=xdefinition of log8.275≈x
See also
Finding Current Value, Calculating Future Value and Modeling a Financial Situation
Finding Current Value
C0=Cn(1+ik)−xC0=Cn(1+ik)x
where
C0:present valueCn:future valuei:annual interest rate in decimal notationk:factor related to the interest periodx:number of interest periods
To ensure the best possible retirement, Christian needs to obtain a future value of $200 000 on an investment he is making today. So what should be the present value of his investment if he knows that it will be subject to an annual interest rate of 2.59 % compounded monthly over a period of 35 years?
See solution
Statistics: Social Choice Theory
Majority Rule
This procedure confers victory on the individual or group that obtains the majority of votes, i.e. 50 %+1 of the total number of votes representing an absolute majority.
In the last Canadian Federal Election, the aim of the various parties was to elect as many deputies as possible from the country's 338 ridings. Once the results have been compiled, here's how power is distributed.
|
Political Party |
Number of Elected Deputies |
|---|---|
|
Conservative Party |
125 |
|
Green Party |
4 |
|
Liberal Party |
171 |
|
New Democratic Party |
16 |
|
Bloc Québécois Party |
22 |
See solution
See also
Plurality Voting
This procedure confers victory on the individual or group that obtains the greatest number of votes, i.e. an absolute majority.
To elect the new captain of the Montreal Canadiens hockey team, the general manager asked the opinion of all the players who have a contract with the team. Each player was asked to write down the name of the player they wanted to lead the team. Here are the results compiled by management.
|
Player |
Number of Votes |
|---|---|
|
Brendan Gallagher |
2 |
|
P.K. Subban |
1 |
|
Max Pacioretty |
16 |
|
David Desharnais |
5 |
|
Tomas Plekanec |
1 |
|
Andrei Markov |
11 |
Using the plurality method, who will be named captain of this team?
See solution
See also
Borda Count
This procedure confers victory on the individual or group who obtains the most points by awarding n−1 points for each voter's 1st choice, n−2 points for the 2nd choice and so on for the next choices n of candidates.
To be inducted into the Hockey Hall of Fame, the players nominated are ranked in order of preference by the members of the Hall committee. To simplify the presentation of the results, votes with identical preferences have been grouped together. Here is the list of four players and their preference ranking in 2014.
|
Choice |
7 Members |
6 Members |
4 Members |
|---|---|---|---|
|
1st choice |
Dominik |
Mike |
Peter |
|
2nd choice |
Peter |
Peter |
Rob |
|
3rd choice |
Mike |
Dominik |
Mike |
|
4th choice |
Rob |
Rob |
Dominik |
Using Borda's method, who would be the next player to be inducted into the Hockey Hall of Fame?
See solution
See also
Condorcet Method
This procedure confers victory on the individual or group that wins all its head-to-head duels according to voters' preferences.
If no individual or group wins all their duels, it is preferable to use another procedure.
To be inducted into the Hockey Hall of Fame, the players nominated are ranked in order of preference by the members of the Hall committee. To simplify the presentation of the results, votes with identical preferences have been grouped together. Here is the list of four players and their preference ranking in 2014.
|
Choice |
7 Members |
6 Members |
4 Members |
|---|---|---|---|
|
1st choice |
Dominik |
Mike |
Peter |
|
2nd choice |
Peter |
Peter |
Rob |
|
3rd choice |
Mike |
Dominik |
Mike |
|
4th choice |
Rob |
Rob |
Dominik |
Using Condorcet's principle, who would be the next player to be inducted into the Hockey Hall of Fame?
See solution
See also
Approval Voting
This procedure confers victory on the individual or group that obtains the highest number of votes while voters can cast their ballot only once for as many candidates as they wish.
In order to avoid the popular vote, the assent vote is used to elect the next class president. Once the results have been counted, the following table is obtained.
| Number of Voters who Voted for these Candidates |
5 |
8 |
10 |
7 |
3 |
|---|---|---|---|---|---|
|
|
Marie-Claude |
Simon |
Vincent |
Judith |
Simon |
|
|
Gitane |
Vincent |
Gitane |
Marie-Claude |
Judith |
|
|
|
Gitane |
Simon |
Vincent |
If we compiled the results properly, who would be the winner of this election if we followed the principle of approval-based voting?
See solution
See also
Elimination Voting
This procedure confers victory on the individual or group that obtains the majority of votes, i.e. 50 %+1 of the total number of votes, while voters rank them in order of preference. If there is no absolute majority on the first count, we eliminate the least popular to transfer votes to the next candidate.
To be inducted into the Hockey Hall of Fame, the players nominated are ranked in order of preference by the members of the Hall committee. To simplify the presentation of the results, votes with identical preferences have been grouped together. Here is the list of four players and their preference ranking in 2014.
|
Choice |
7 Members |
6 Members |
4 Members |
|---|---|---|---|
|
1st choice |
Dominik |
Mike |
Peter |
|
2nd choice |
Peter |
Peter |
Dominik |
|
3rd choice |
Mike |
Dominik |
Mike |
Using the elimination voting method, who would be the next player to be inducted into the Hockey Hall of Fame?
See solution
See also
Graphs
To fully understand the concepts in this section, it is important to master the following vocabulary.
-
Vertices : the different elements which are linked (people, steps to be taken, etc.) and which are generally represented by dots.
-
Edges : the links that connect the elements, generally represented by lines or arcs.
-
Parallel edges : when two edges have the same start and end vertices.
-
Loop : edge which begins and ends with the same vertex.
-
Degree : the number of times a vertex is touched by the different edges.
-
Chain : a sequence of edges that we loan to ‘walk’ around the graph.
-
Length : corresponds to the number of edges loaned in a chain.
-
Distance : minimum number of stops to go from the starting vertex to the destination vertex.
-
Simple chain : a chain in which each edge is loaned only once.
-
Cycle : a chain that starts and ends at the same vertex.
-
Simple cycle : a cycle in which each edge is used only once.
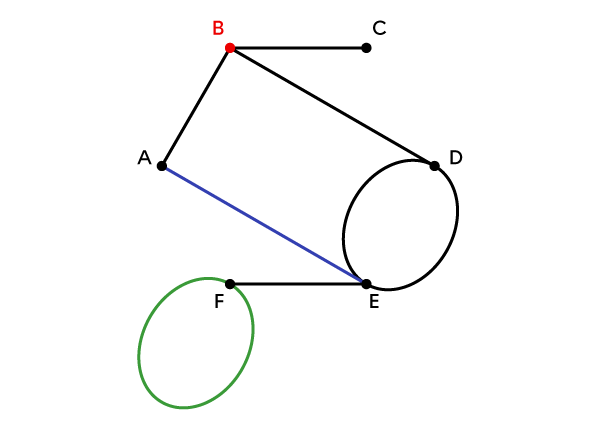
B is a vertex.
A—E is an edge.
F—F is a loop.
E—D and D—E are parallel edges.
The degree of B is 3.
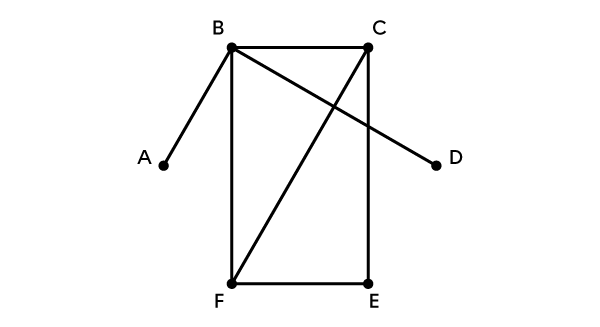
B−F−E−C−F−B is a cycle.
D−B−C−B−A is a chain.

A−B−C−F is a simple string of length 3, but the distance d(A,F)=2.
Finally, A−B−C−F−E−A is a simple cycle of length 5.
See also
Eulerian Chains and Cycles
The Eulerian characteristic of a graph requires that all edges are involved only once in the chain or cycle.
As a police officer, you want to know every nook and cranny of the area you serve. To do this, you decide to patrol every street in your district during your shift. To help you, you use a road map to identify the area you have to supervise.
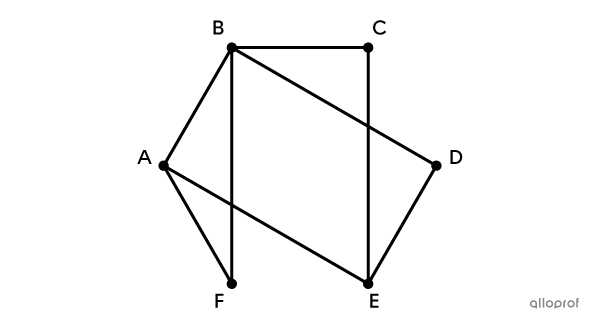
Bearing in mind that you can decide where your route starts and finishes, what sequence of routes should you take to patrol each street as efficiently as possible?
See solution
See also
Hamiltonian Chains and Cycles
The Hamiltonian characteristic of a graph requires that all the vertices are involved only once in the chain or cycle.
To complete a car rally, competitors must pass through each of the milestones identified by letters on the following map.
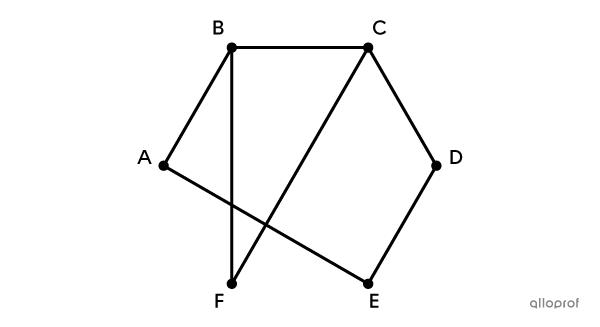
Bearing in mind that they must return to the starting point identified by the vertex A to finish the race, what could be one of the routes taken by the competitors?
See solution
See also
Types of Graphs
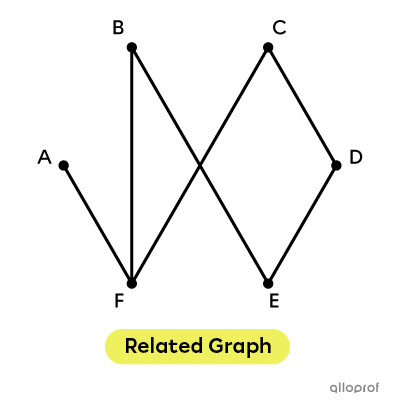
Depending on the information provided on the graph, it can be given a specific name.
-
Related : when all the vertices are accessible from any vertex.
-
Tree : it's a graph that has no simple cycles.
-
Oriented : when the edges suggest an accurate orientation by means of an arrow.
-
Weighted (Valued) : when each of the edges has a quantity associated with it.
-
Coloured : when each of the edges has a quantity associated with it.




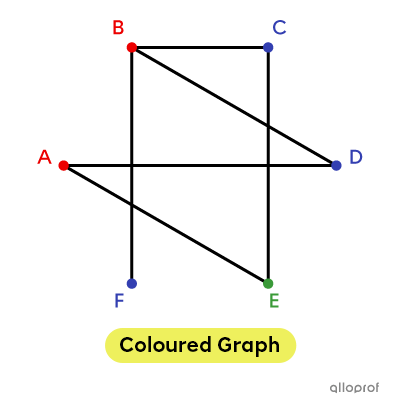
See also
Critical Path
In practical terms, the critical path is often used to establish a deadline for completing a project.
Before you buy a home, it's important to analyse a number of factors that will help you make a wise purchase. To make sure you don't forget anything in the process, here are a few tips.
|
Tasks |
Time (Days) |
Prerequisites |
|---|---|---|
|
A : Establishing your needs |
1 |
None |
|
B : Drawing up a budget |
5 |
A |
|
C : Shopping for a mortgage |
7 |
B |
|
D : Hiring a notary |
3 |
B |
|
E : Hiring a real estate agent |
3 |
B |
|
F : Visiting homes |
182 |
C - D - E |
|
G : Negotiating an interest rate |
7 |
F |
|
H : Obtain a pre-authorised loan |
30 |
F |
|
I : Making an offer |
7 |
G - H |
|
J : Have the home inspected |
14 |
I |
|
K : Signing the deed of sale |
2 |
J |
|
L : Taking out home insurance |
10 |
J |
|
M : Moving |
1 |
K - L |
What is the total duration of such a project?
See solution
See also
Chromatic Number
In practical terms, the chromatic number is often used to colour a world map, design electronic chips or plan a telecommunications network.
Keen to get to know her colleagues as well as possible, Ms Dreau wants to take part in as many of the activities offered by her school as possible. However, certain constraints in her timetable prevent her from taking part in everything she would like to.
-
journalism clashes with a few improvisation and success support sessions;
-
it's impossible for her to enrol in basketball, theatre and dance at the same time;
-
success support and theatre are both on the Monday evening timetable.
What is the maximum number of activities she can take part in?
See solution
See also
Weighted Trees
In practical terms, the weighted tree is often used to minimise or maximise costs or distances.
Before building homes in a new neighbourhood, a city must install a water and sewer system that connects each residence. Despite a few geographical constraints, most homes can be connected by this future system.
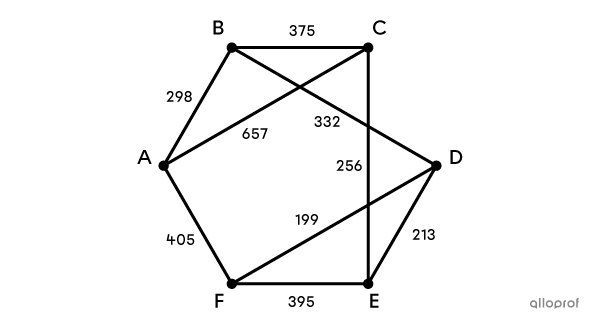
Taking the quantities in the graph as the distance, in metres, between each of the houses, what would be the minimum length of the network in this neighbourhood?
See solution
- Top of page
- Algebra
- First Degree Linear Function (Functional and General Form)
- Solving a System of Equations Using Comparison
- Solving a System of Equations Using Substitution
- Solving a System of Equations Using Elimination
- Optimization
- Probability
- Types of Events
- The Odds For and the Odds Against
- Mathematical Expectation (Fair Games)
- Conditional Probability
- Geometry
- Equivalent Figures
- Equivalent Solids
- Financial Mathematics
- Properties of Exponential Notation
- Definitions and Laws of Logarithmic Notation
- Finding Current Value, Calculating Future Value and Modeling a Financial Situation
- Statistics: Social Choice Theory
- Majority Rule
- Plurality Voting
- Borda Count
- Condorcet Method
- Approval Voting
- Elimination Voting
- Graphs
- Eulerian Chains and Cycles
- Hamiltonian Chains and Cycles
- Types of Graphs
- Critical Path
- Chromatic Number
- Weighted Trees
