Subjects
Grades
The hyperbola is one of the conics. It is obtained by the intersection of a cone and a plane perpendicular to the base of the conic.
A hyperbola is the geometric locus of all points whose difference of distances to 2 fixed points, called foci, is constant.
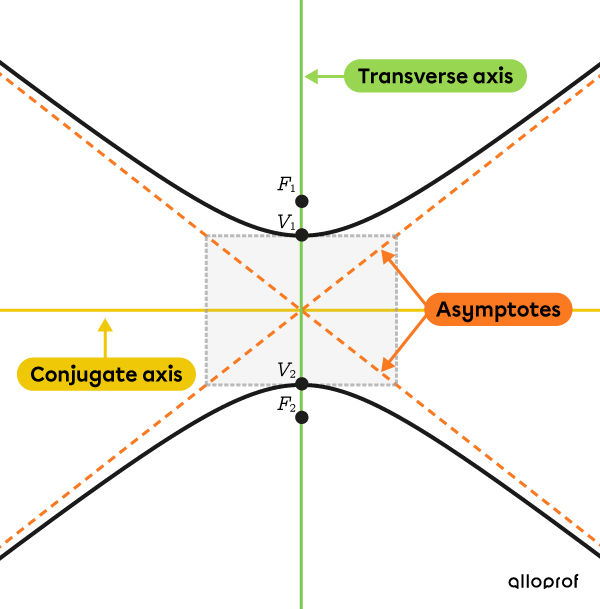
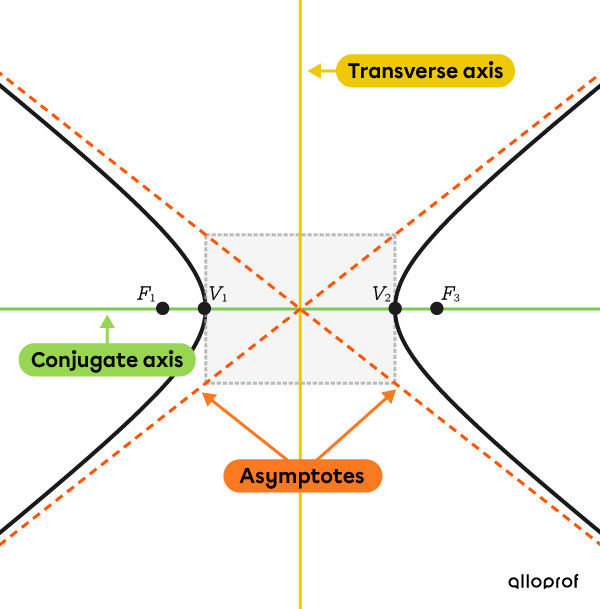
A hyperbola has two vertices, |V_1| and |V_2.|
A hyperbola has two foci, |F_1| and |F_2.|
A hyperbola has two asymptotes.
The transverse axis is the line intersecting the two foci and two vertices.
The conjugate axis is the line perpendicular to the transverse axis that passes through the point where the asymptotes intersect.
We can form a rectangle where two sides of the rectangle pass through the vertices of the hyperbola and the vertices of the rectangle intersect its asymptotes.
A hyperbola can be vertical or horizontal.
A hyperbola is vertical when the transverse axis is vertical.
A hyperbola is horizontal when the transverse axis is horizontal.
The equation that defines a hyperbola centred at the origin uses parameters |a| and |b.| There are two different equations, depending on its orientation. We must also determine the equation of the straight lines constituting the asymptotes of the curve.
||\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=-1|| where ||\begin{align} a&:\text{Half the rectangle’s width}\\ b&:\text{The distance between the vertex and its centre} \end{align}||
||\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1|| where ||\begin{align} a&:\text{The distance between the vertex and its centre}\\ b&:\text{Half the height of the rectangle}\end{align}||
||\begin{align}\text{Increasing asymptote:}\ \ y&=\dfrac{b}{a}x\\\\ \text{Decreasing asymptote:}\ \ y&=-\dfrac{b}{a}x\end{align}||
We place the term in |x| first and the term in |y| second, separated by a subtraction. The equation of the vertical hyperbola is equal to |-1| and the horizontal hyperbola is equal to |1.|
Here are the graphical representations of the two types of hyperbolas centred at the origin on which the vertices, foci, and asymptotes are placed.
The points where the difference of the distances to two fixed points (foci) is |2\color{#3b87cd}b.|
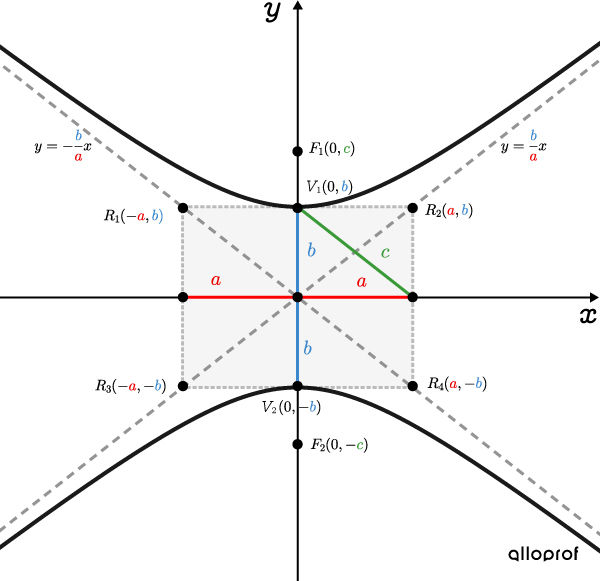
The points where the difference of the distances to two fixed points (foci) is |2\color{#ec0000}a.|
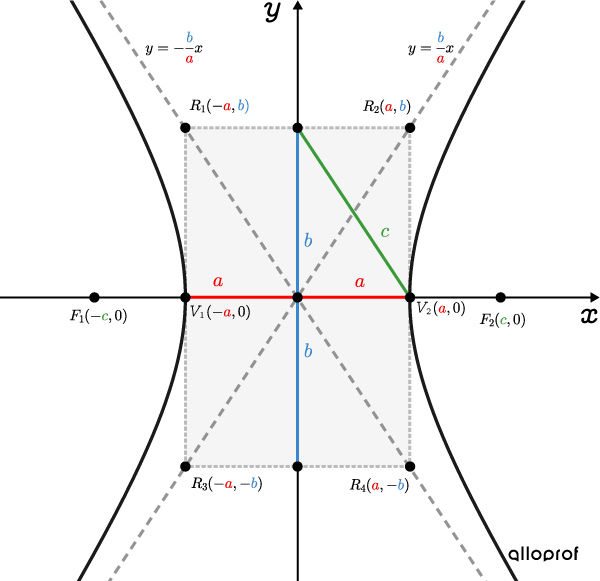
The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
To determine the equation of a hyperbola centred at the origin, find the value of parameters |a| and |b.|
Generally, the following procedure is used.
Choose the right form of the equation according to the orientation of the hyperbola.
Use the information provided with respect to the vertices to determine the value of parameter |\color{#ec0000}a| and/or parameter |\color{#3B87CD}b.|
Use one of the following strategies to determine the missing parameter, if there is one:
a) If parameter |\color{#3A9A38}c| (the distance between the centre and a focus) is provided, use the Pythagorean Theorem. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
b) If point |(x,y)| belonging to the hyperbola is provided, substitute its coordinates in the hyperbola equation.
c) If point |(x,y)| belonging to one of the asymptotes is provided, substitute its coordinates into the asymptote equation.
d) If the equation of one of the asymptotes is provided, use the rate of change |\dfrac{\color{#3b87cd}b}{\color{#ec0000}a}.|
Write the hyperbola’s equation.
Here is an example where vertex and focus are provided.
Determine the equation of the hyperbola.
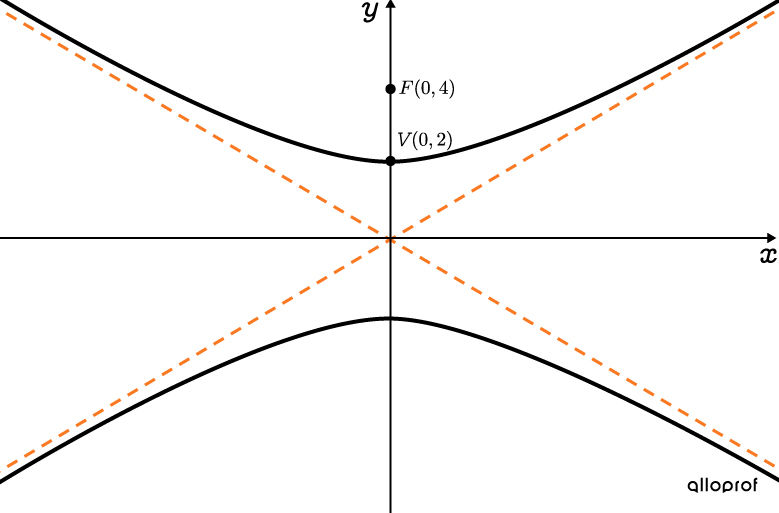
Here is an example where the vertex and a point |(x,y)| belonging to the asymptotes are provided.
Determine the equation of a hyperbola where one of its points on the transverse axis is |(-3,0)| and one of its asymptotes intersects the point |\left(-2,\dfrac{10}{3}\right).|
Follow these steps to graph a hyperbola centred at the origin using its equation.
Place the centre of the hyperbola and determine its orientation.
Draw the rectangle of the hyperbola where its vertices correspond to: ||\begin{align}&R_1(-\color{#ec0000}a,\color{#3b87cd}b)&&R_2(\color{#ec0000}a,\color{#3b87cd}b)\\&R_3(-\color{#ec0000}a,-\color{#3b87cd}b)&&R_4(\color{#ec0000}a,-\color{#3b87cd}b)\end{align}||
Draw the asymptotes by extending the rectangle’s diagonals.
Place the hyperbola’s vertices. ||\begin{align}\\ &\text{Vertical hyperbola}&&\text{Horizontal hyperbola}\\&V_1(0,\color{#3b87cd}b)&&V_1(-\color{#ec0000}a,0)\\&V_2(0,-\color{#3b87cd}b)&&V_2(\color{#ec0000}a,0)\end{align}||
Draw the hyperbola such that it passes through the vertices and approaches the asymptotes without ever touching them.
Draw the hyperbola represented by the following equation. ||\dfrac{x^2}{81}-\dfrac{y^2}{16}=-1||
Here is an animation to help you understand the different relationships and the role of parameters in the hyperbola.
The equation that defines the transformed hyperbola uses the parameters |a,| |b,| |h,| and |k.| As with a hyperbola centred at the origin, two different equations can be distinguished according to its orientation. The equation of the lines constituting the asymptotes of the curve must also be determined.
||\dfrac{(x-h)^{2}}{a^{2}}-\dfrac{(y-k)^{2}}{b^{2}}=-1|| where ||\begin{align} a &:\text{half the width of the rectangle}\\ b &: \text{the distance between the vertex and centre} \\ (h,k)&:\text{The centre’s coordinates}\\&\phantom {:}\ \ \text{(intersection of the asymptotes)}\end{align}||
||\dfrac{(x-h)^{2}}{a^{2}}-\dfrac{(y-k)^{2}}{b^{2}}=1|| where ||\begin{align} a &:\text{The measure between the vertex and centre}\\ b &: \text{half the height of the rectangle} \\ (h,k)&:\text{The centre’s coordinates}\\&\phantom {:}\ \ \text{(intersection of the asymptotes)}\end{align}||
||\begin{align}\text{Increasing asymptote:}\ \ y&=\dfrac{b}{a}(x-h)+k\\\\ \text{Decreasing asymptote:}\ \ y&=-\dfrac{b}{a}(x-h)+k\end{align}||
Here are the graphical representations of the two types of hyperbolas not centred at the origin where the vertices, foci, and asymptotes are placed.
The points where the difference of the distances to two fixed points (foci) is |2\color{#3b87cd}b.|
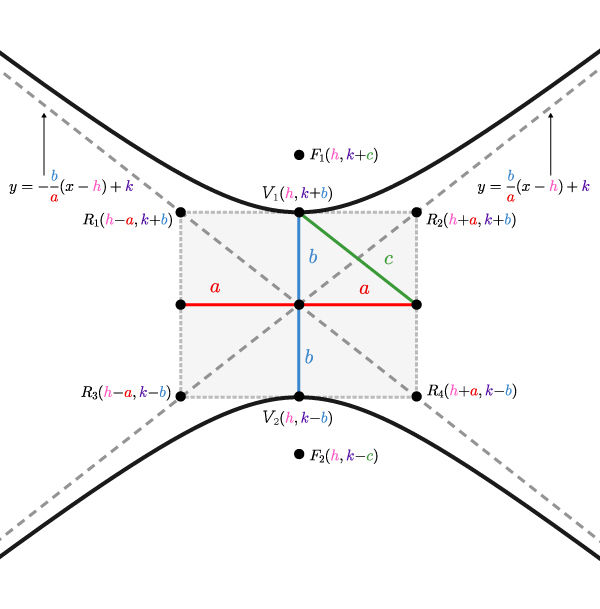
The points where the difference of the distances to two fixed points (foci) is |2\color{#ec0000}a.|
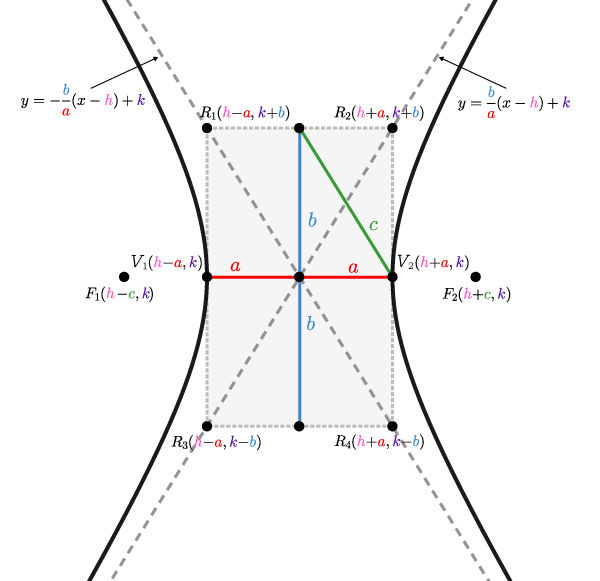
The relationship between parameters |\color{#ec0000}a,| |\color{#3b87cd}b,| and |\color{#3a9a38}c| can be expressed using the Pythagorean Theorem. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
To determine the equation of a hyperbola not centred at the origin from a graph, find the value of the parameters |a,| |b,| |h,| and |k.|
Generally, the following procedure is used.
Choose the right form of the equation according to the orientation of the hyperbola.
Determine the value of parameters |\color{#FF55C3}h| and |\color{#560FA5}k| from the coordinates at the centre of the hyperbola.
Use the information provided in respect to the vertices to determine the value of the parameter |\color{#ec0000}a| and/or parameter |\color{#3B87CD}b| according to the orientation of the hyperbola.
Determine the missing parameter with one of the strategies below:
a) If parameter |\color{#3A9A38}c| (the distance between the centre and a focus) is provided, use the Pythagorean Theorem. ||\color{#3a9a38}c^2=\color{#ec0000}a^2+\color{#3b87cd}b^2||
b) If point |(x,y)| belonging to the hyperbola is provided, substitute its coordinates in the hyperbola’s equation.
c) If point |(x,y)| belonging to one of the asymptotes is provided, substitute its coordinates in the asymptote’s equation.
d) If the equation of one of the asymptotes is provided, use the rate of change |\dfrac{\color{#3b87cd}b}{\color{#ec0000}a}.|
Write the hyperbola’s equation.
Here is an example where a vertex and point |(x,y)| belonging to the hyperbola are provided.
Determine the hyperbola’s equation.

Here is an example where a vertex and the equation of one of the asymptotes are provided.
Determine the equation of a vertical hyperbola where one of the vertices is located at point |(0,16)| and where one of the asymptotes has the equation |y=\dfrac{6}{5}x-8.|
Follow these steps to graph a hyperbola not centred at the origin using its equation.
Identify parameters |\color{#FF55C3}h| and |\color{#560FA5}k| in the equation and place the centre of the hyperbola.
Draw the rectangle of the hyperbola whose vertices correspond to: ||\begin{align}&R_1(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k+\color{#3b87cd}b)&&R_2(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k+\color{#3b87cd}b)\\&R_3(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k-\color{#3b87cd}b)&&R_4(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k-\color{#3b87cd}b)\end{align}||
Draw the asymptotes by extending the diagonals of the rectangle.
Place the hyperbola’s vertices. ||\begin{align}\\ &\text{Vertical Hyperbola}&&\text{Horizontal Hyperbola}\\&V_1(\color{#ff55c3}h,\color{#560fa5}k+\color{#3b87cd}b)&&V_1(\color{#ff55c3}h-\color{#ec0000}a,\color{#560fa5}k)\\&V_2(\color{#ff55c3}h,\color{#560fa5}k-\color{#3b87cd}b)&&V_2(\color{#ff55c3}h+\color{#ec0000}a,\color{#560fa5}k)\end{align}||
Draw the hyperbola such that it passes through the vertices and approaches the asymptotes without ever touching them.
Draw the hyperbola represented by the following equation. ||\dfrac{(x-5)^{2}}{64}-\dfrac{(y+4)^{2}}{100}=1||
When we want to represent a region bounded by a hyperbola, we apply the following relationships.
|
Vertical hyperbola |
|
|---|---|
|
Graphical Representation |
Corresponding Inequality |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}>-1\\\\\dfrac{(x-h)^2}{a^2}&-\frac{(y-k)^2}{b^2}>-1\end{align}|| |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}<-1\\\\\dfrac{(x-h)^2}{a^2}&-\dfrac{(y-k)^2}{b^2}<-1\end{align}|| |
|
Horizontal hyperbola |
|
|
Graphical Representation |
Corresponding Inequality |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}<1\\\\\dfrac{(x-h)^2}{a^2}&-\dfrac{(y-k)^2}{b^2}<1\end{align}|| |
 |
||\begin{align}\dfrac{x^{2}}{a^{2}}&-\dfrac{y^{2}}{b^{2}}>1\\\\\dfrac{(x-h)^2}{a^2}&-\dfrac{(y-k)^2}{b^2}>1\end{align}|| |
To include the points that are on the hyperbola, change the inequality symbols |<, >| to the symbols |\geq, \leq,| respectively.