Equivalent Fractions | Elementary

A fraction is equivalent to another fraction when it represents the same part of a whole or set.

To fully understand what an equivalent fraction is, first you need to understand the role of the numerator and the denominator. To learn what a numerator and a denominator are, see The Representation of a Fraction.

It is important for the wholes to be identical - that is to say, they are the same size, as in the following image.

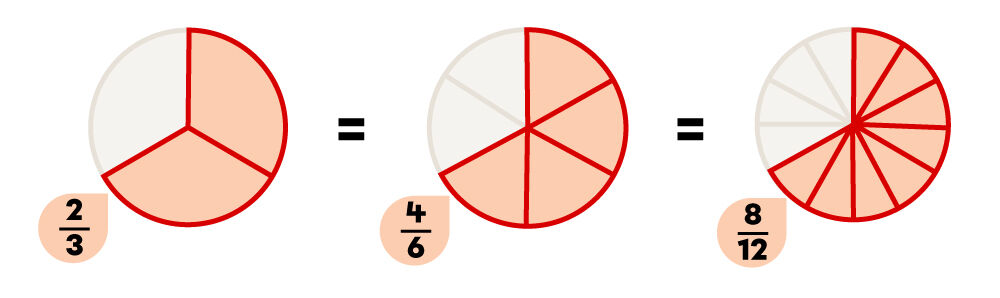
In this picture you can see that |2| parts out of |3| is equivalent to |4| parts out of |6| or |8| parts out of |12.| Thus, the amount shaded or used represents the same portion of the whole in each example.

To verify that fractions are equivalent, I need to complete the following steps:

1. I represent the fraction of my choice.

2. I represent the second fraction using the same whole or set.

3. I compare the two fractions by observing the amounts used or shaded.

Alicia baked |12| cupcakes. |\dfrac{1}{3}| of her cupcakes have red frosting and  |\dfrac{3}{12}| have blue frosting. All of the remaining cupcakes are white.

Did Alicia bake the same number of red cupcakes as blue cupcakes?

I represent the fraction of my choice. First, I choose to represent the fraction |\dfrac{3}{12}.| I know the total amount of cupcakes is |12| and the number of blue cupcakes is |\dfrac{3}{12}.|
I represent the second fraction using the same total. I know the total amount of cupcakes is |12| and that the quantity of red cupcakes is |\dfrac{1}{3}| of the total. Therefore, I need to divide the total amount of cupcakes into three equal groups and then pick one of the |3| groups.
I compare the two fractions by checking the quantities used or shaded. The first fraction indicates that Alicia made |3| blue cupcakes and the second fraction indicates she made |4| red cupcakes.

The amount of red cupcakes is not equivalent to the amount of blue cupcakes, because Alicia frosted |4| cupcakes red and only |3| cupcakes blue.

Therefore, |\dfrac{3}{12}| is not equivalent to |\dfrac{1}{3}.|

A fraction is equivalent to another fraction when it represents the same part of a whole or set.

To fully understand what an equivalent fraction is, first you need to understand the role of the numerator and the denominator. To learn what a numerator and a denominator are, see The Representation of a Fraction.

It is important for the wholes to be identical - that is to say, they are the same size, as in the following image.

In this picture you can see that |2| parts out of |3| is equivalent to |4| parts out of |6| or |8| parts out of |12|. Thus, the amount shaded represents the same portion of the whole in each example.

To find an equivalent fraction using multiplication, I need to complete the following steps:

1. I determine by what number to multiply the fraction.

2. I multiply the numerator by that number.

3. I multiply the denominator by the same number.

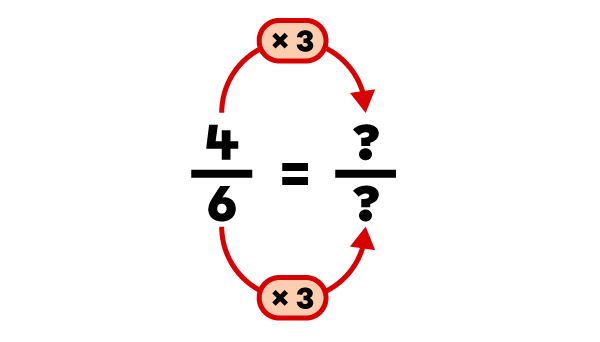
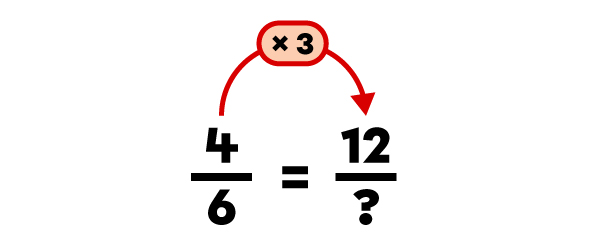
Find a fraction equivalent to |\dfrac{4}{6}| using multiplication.

I determine by what number I want to multiply the fraction. Here, I choose to multiply the fraction by |3.|
I multiply the numerator by that number.
I multiply the denominator by the same number.

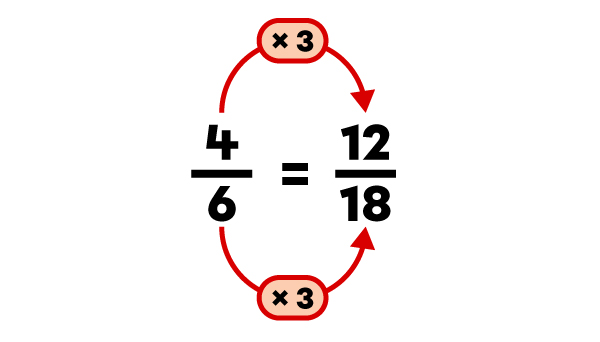|\dfrac{12}{18}| is an equivalent fraction to |\dfrac{4}{6}.|

To find an equivalent fraction using division, I need to complete the following steps:

1. I determine the number I want to divide the fraction by.

2. I divide the numerator by that number.

3. I divide the denominator by the same number.

Find a fraction equivalent to |\dfrac{4}{6}| by using division.

I determine the number I want to divide the fraction by. I need to make sure that the numerator and the denominator are both divisible by the number I choose. I know that both |4| and |6| are divisible by |2.|
I divide the numerator by that number.
I divide the denominator by the same number.

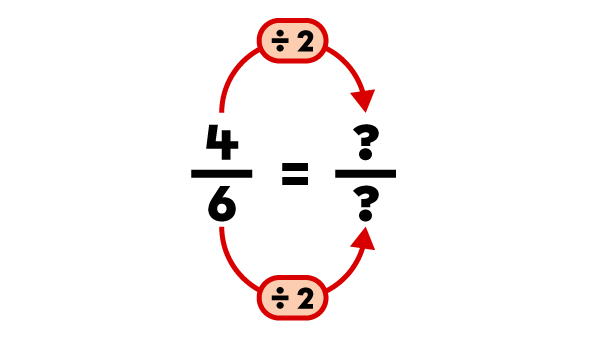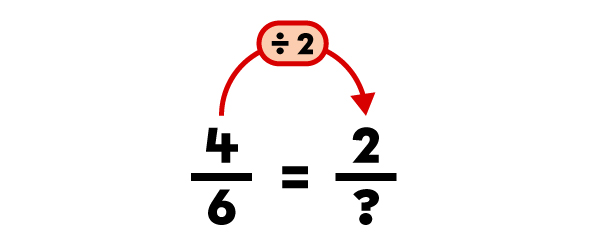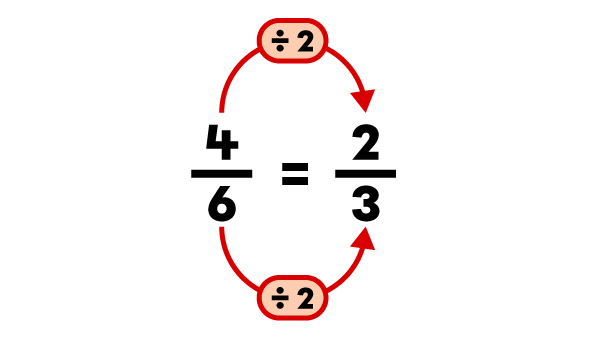|\dfrac{2}{3}| is an equivalent fraction to |\dfrac{4}{6}.|