
Le rôle des paramètres dans une fonction logarithmique
Secondaire 4-5
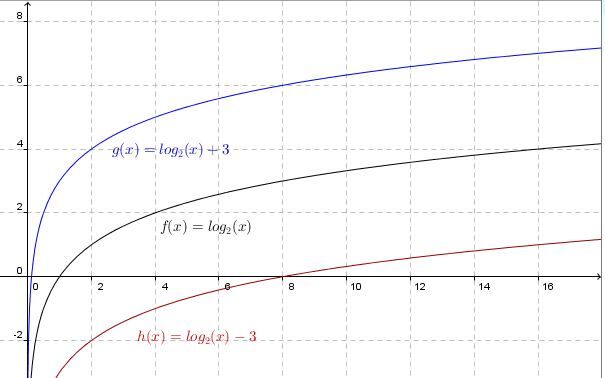
Lorsqu’on ajoute les paramètres |a,| |b,| |h| et |k| à la forme de base |f(x)= \log_c x,| on obtient ce qu'on appelle la forme canonique (aussi appelée forme transformée) de la fonction logarithmique.
La fonction logarithmique transformée s'écrit habituellement de la façon suivante : ||f(x)=a \log_c (b(x-h)) +k||où |a,b,h,| et |k| sont des nombres réels jouant le rôle de paramètres.
Remarques : Les paramètres |a| et |b| sont toujours différents de zéro.
La base de la fonction |(c)| doit être supérieure à |0| et différente de |1.|
Manipulation animée des paramètres
Dans l'animation interactive suivante, tu peux modifier les paramètres |a|, |b|, |c|, |h| et |k| de la fonction logarithmique. Observe bien les modifications qui s'opèrent sur la courbe transformée (en noir) par rapport à la fonction de base avec |c=2| (en vert). Tu peux en profiter pour observer l'effet de la modification des paramètres sur les propriétés de la fonction.
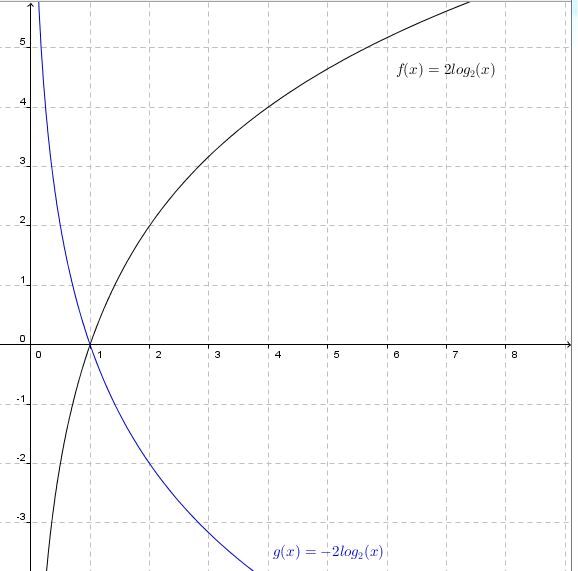
L'analyse du paramètre |a|a
Un changement d'échelle vertical à la fonction de facteur |a|a
Lorsque |a>1| :
Le graphique s'étire verticalement par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre a est grande, plus la courbe de la fonction log s'éloigne de l’axe des x.
Lorsque |0< a <1| :
Le graphique se contracte verticalement par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre a est petite (près de 0), plus la courbe de la fonction log se rapproche de l’axe des x.

Une réflexion de la courbe de la fonction autour de l'axe des |x|x
Lorsque |a| est positif |a>0| :
La courbe de la fonction logarithmique est croissante.
Lorsque |a| est négative |a<0| :
La courbe de la fonction logarithmique est décroissante.
L'analyse du paramètre |b|b
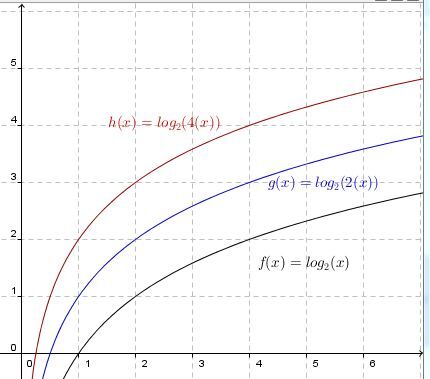
Un changement d'échelle horizontal de la fonction de facteur |\dfrac{1}{b}|1b
Lorsque |b>1| :
Le graphique se contracte horizontalement par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre |b| est grande, plus la courbe de la fonction logarithme se rapproche de l’axe des |y|.
Lorsque |0<b<1| :
Le graphique s'étire horizontalement par rapport à la fonction de base. En effet, plus la valeur absolue du paramètre |b| est petite (près de 0), plus la courbe de la fonction logarithme s'éloigne de l’axe des |y|.
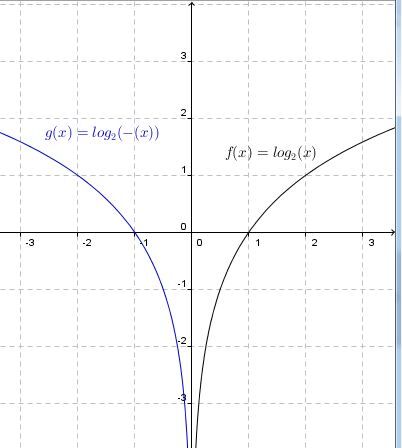
Une réflexion de la courbe de la fonction autour de l'axe des |y|y
Lorsque |b| est positif |b>0| :
La courbe de la fonction logarithmique est orientée vers la droite, c'est-à-dire qu'elle est entièrement située à la droite de l'asymptote.
Lorsque |b| est négatif |b<0| :
La courbe de la fonction logarithmique est orientée vers la gauche, c'est-à-dire qu'elle est entièrement située à la gauche de l'asymptote.
L'analyse de la base |c|c
La variation de la fonction
La valeur de |c| représente la base de la fonction, c'est-à-dire le facteur multiplicatif présent dans la fonction exponentielle.
Lorsque |c>1| :
La fonction de base est croissante.
Lorsque |0<c<1| :
La fonction de base est décroissante.
Important!
Il est utile de remarquer que |\log_c x = -\log_{\frac{1}{c}} x|.
En utilisant cette propriété, il est possible de transformer un logarithme ayant une base entre 0 et 1 en un logarithme ayant une base supérieure à 1.
Soit une fonction logarithmique dont la règle est |f(x)=3\log_4x.| Selon la propriété |\log_cx=-\log_{\frac{1}{c}}x,| on peut déduire la règle d’une fonction équivalente à |f(x).|||\begin{align}f(x)&=3\log_4x \\\\&= \color{#EC0000}{-}3\log_{\color{#333FB1}{\frac{1}{4}}}x\end{align}||L’égalité entre les deux règles s’explique par le fait que rendre le paramètre |a| négatif provoque le même effet sur le graphique qu’inverser la valeur du paramètre |c.|
-
S’il est négatif, le paramètre |a| provoque une réflexion par rapport à l’axe des |x.|
-
S’il est entre |0| et |1,| le paramètre |c| provoque une réflexion par rapport à l’axe des |x.|
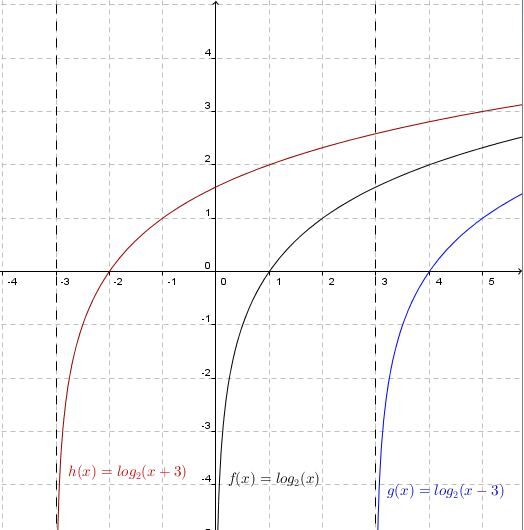
L'analyse du paramètre |h|h
Une translation horizontale de toute la fonction
Lorsque |h| est positif |h>0| :
La courbe de la fonction logarithmique se déplace vers la droite.
Lorsque |h| est négatif |h<0| :
La courbe de la fonction logarithmique se déplace vers la gauche.
Important!
L'asymptote de la fonction logarithmique a pour équation |x = h.| Par conséquent, si la valeur du paramètre |h| est modifiée, l'emplacement de l'asymptote est également modifié.
L'analyse du paramètre |k|k
Une translation verticale de toute la fonction
Lorsque |k| est positif |k>0| :
La courbe de la fonction logarithmique se déplace vers le haut.
Lorsque |k| est négatif |k<0| :
La courbe de la fonction logarithmique se déplace vers le bas.
Résumé
Si |c>1:|
| |a>0| | |a<0| | |
|---|---|---|
| |b>0| | 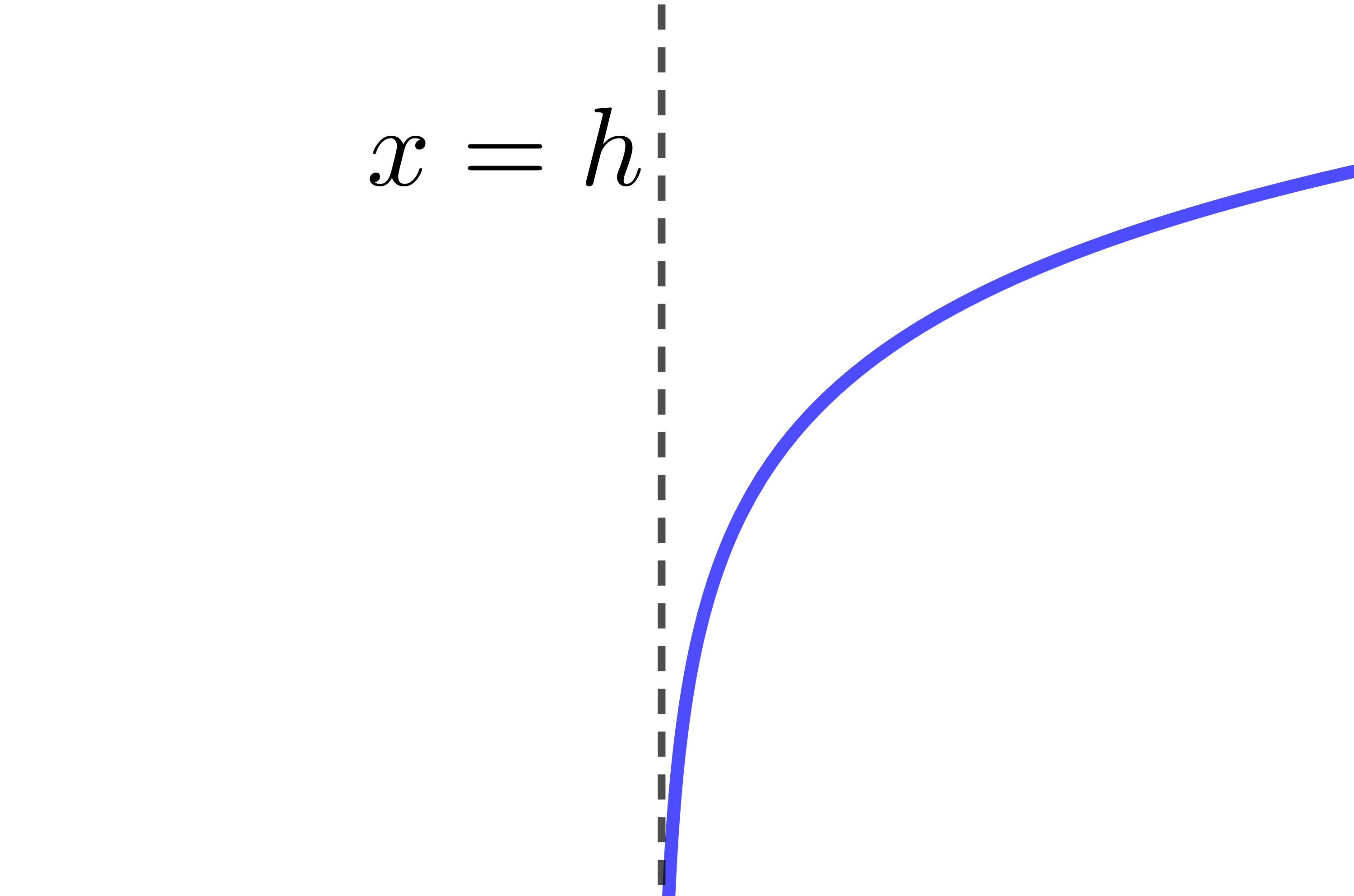 |
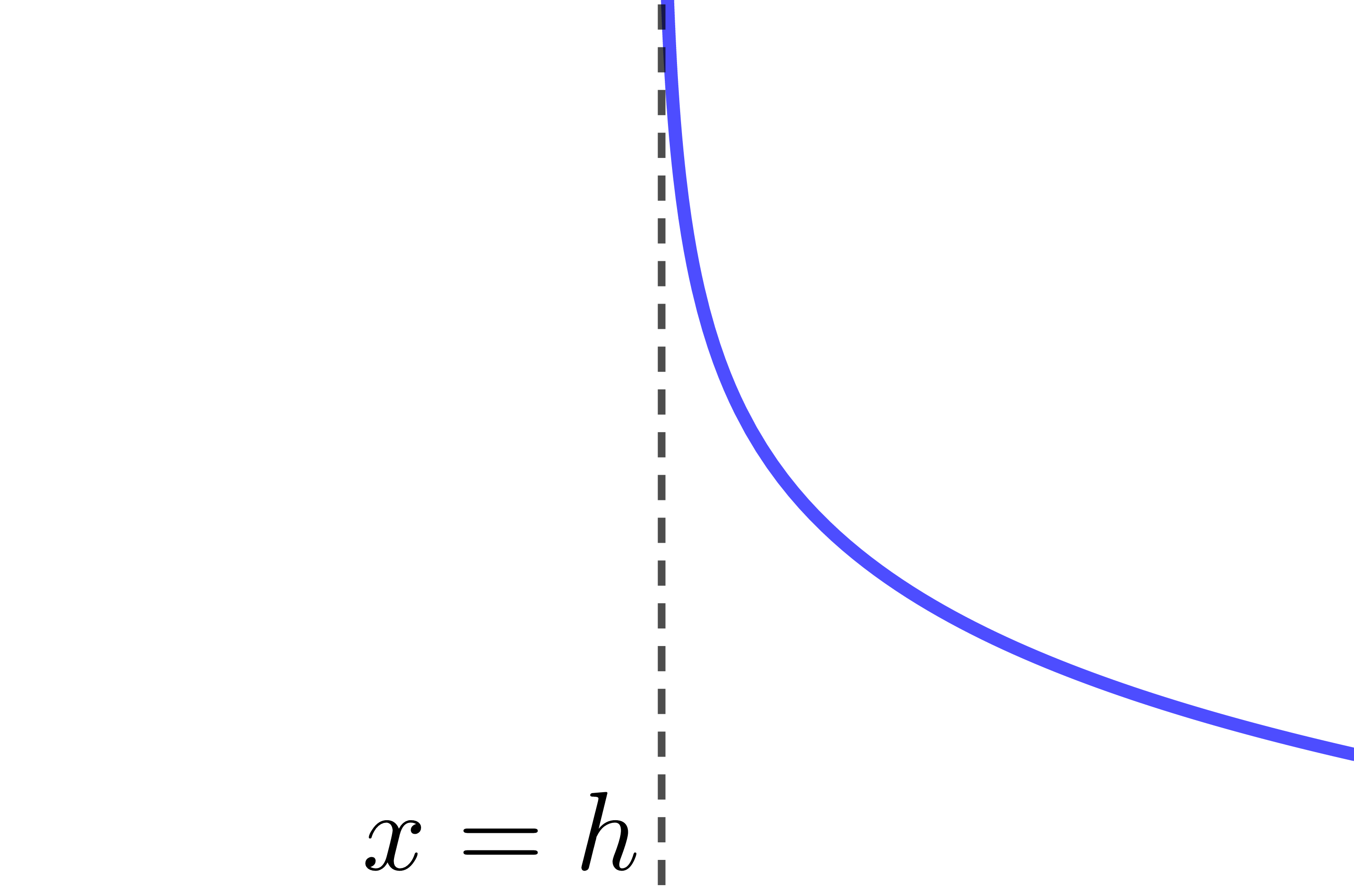 |
| |b<0| | 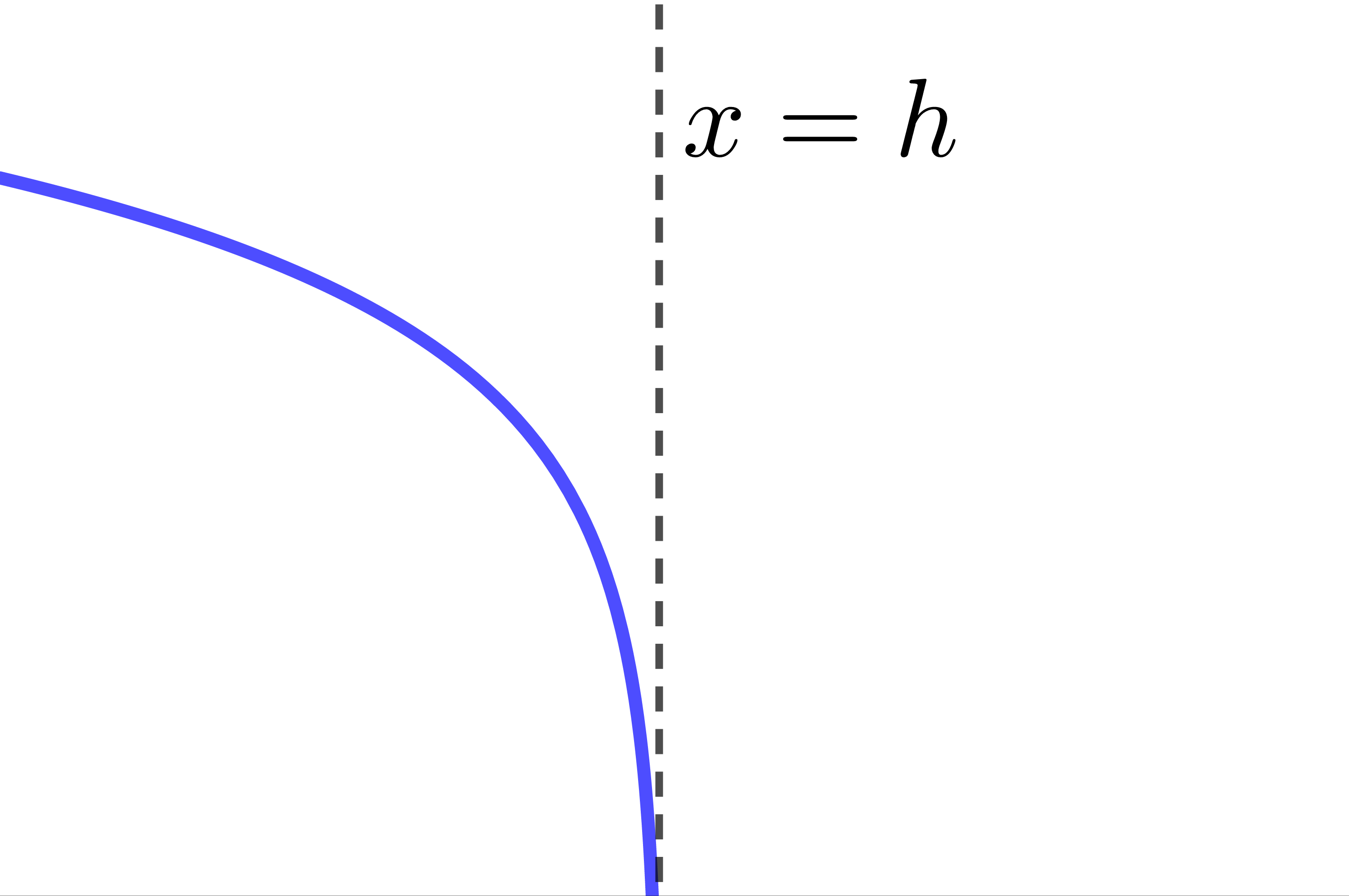 |
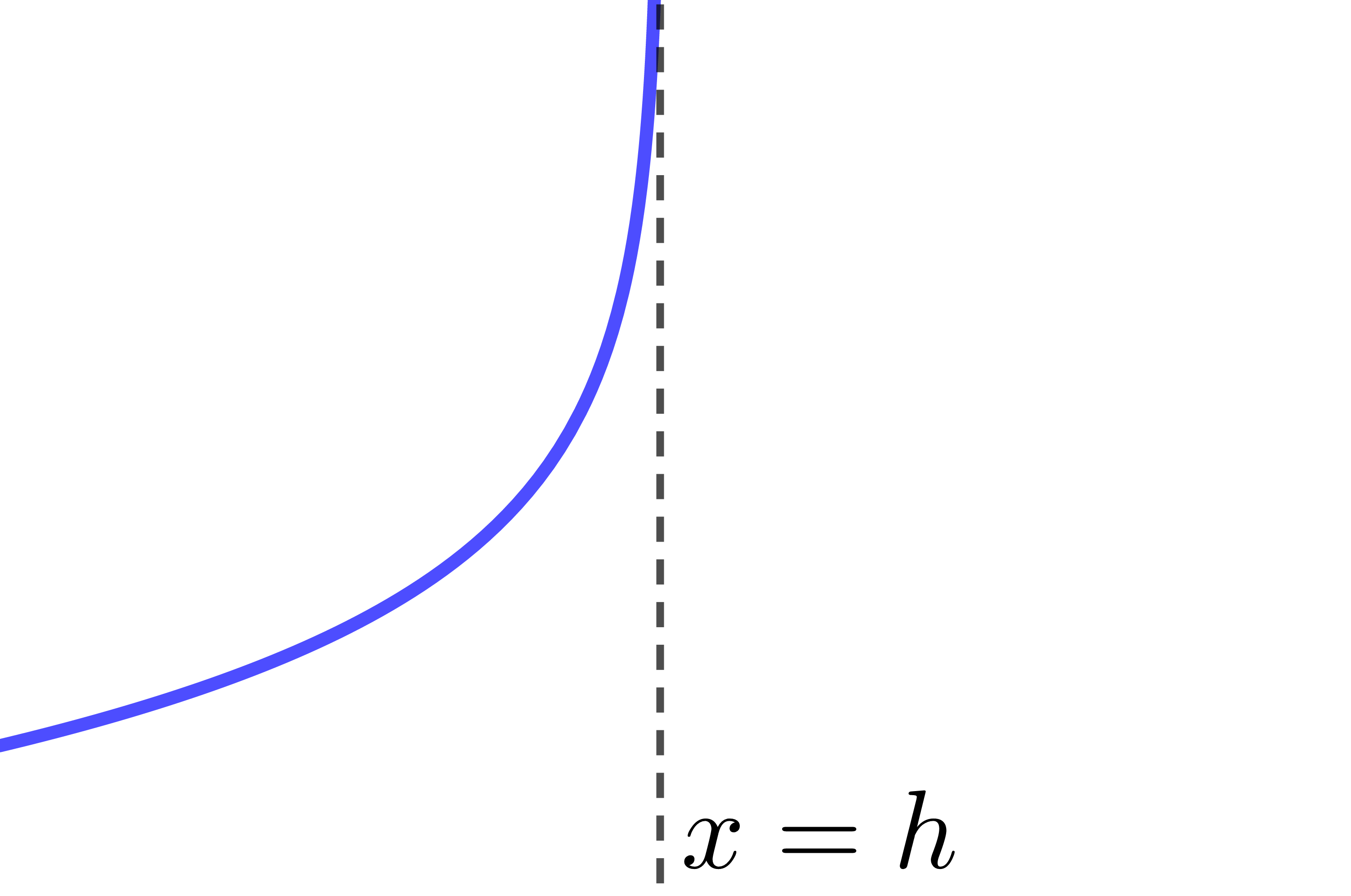 |
Si |0<c<1:|
| |a>0| | |a<0| | |
|---|---|---|
| |b>0| | 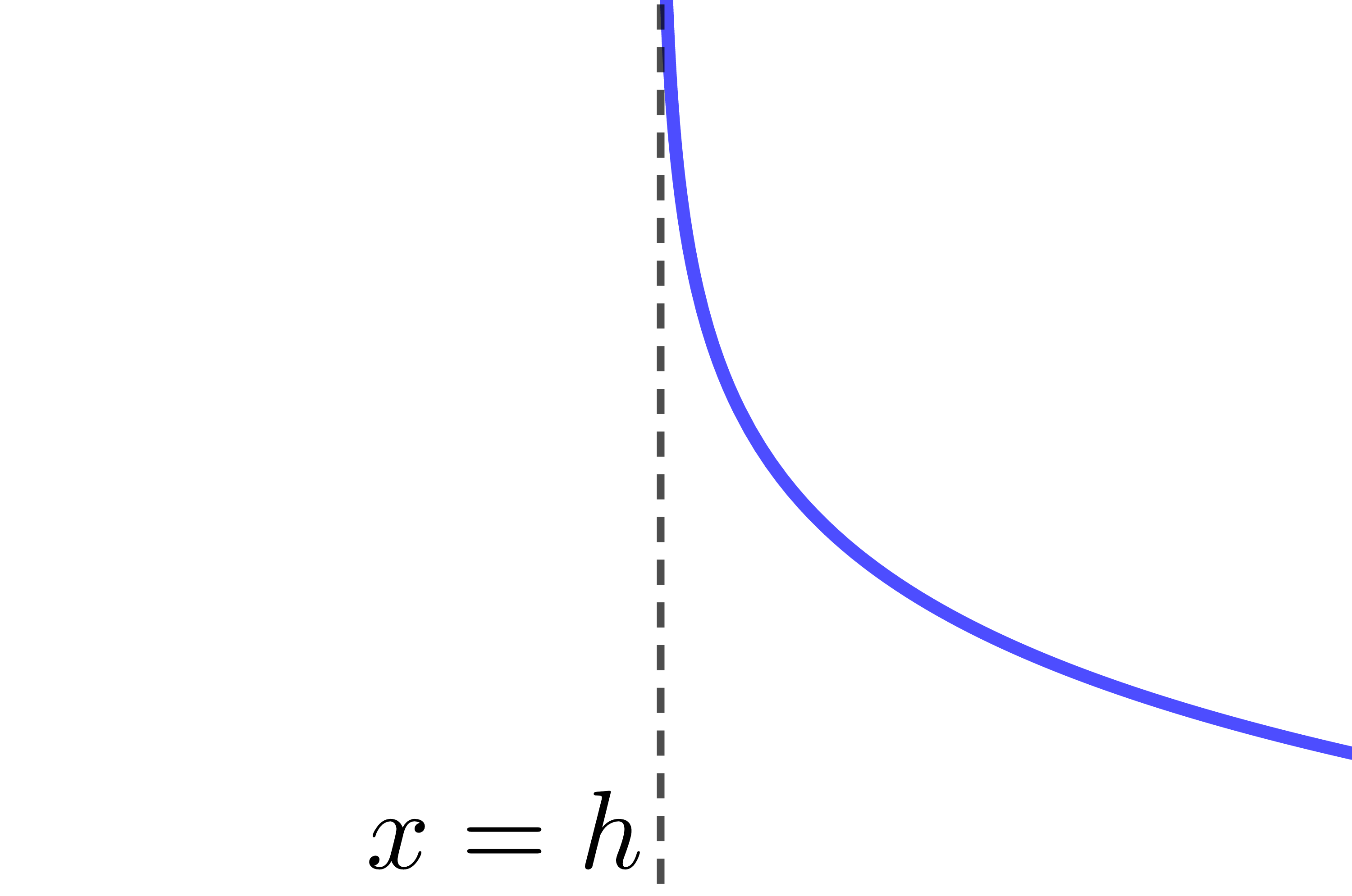 |
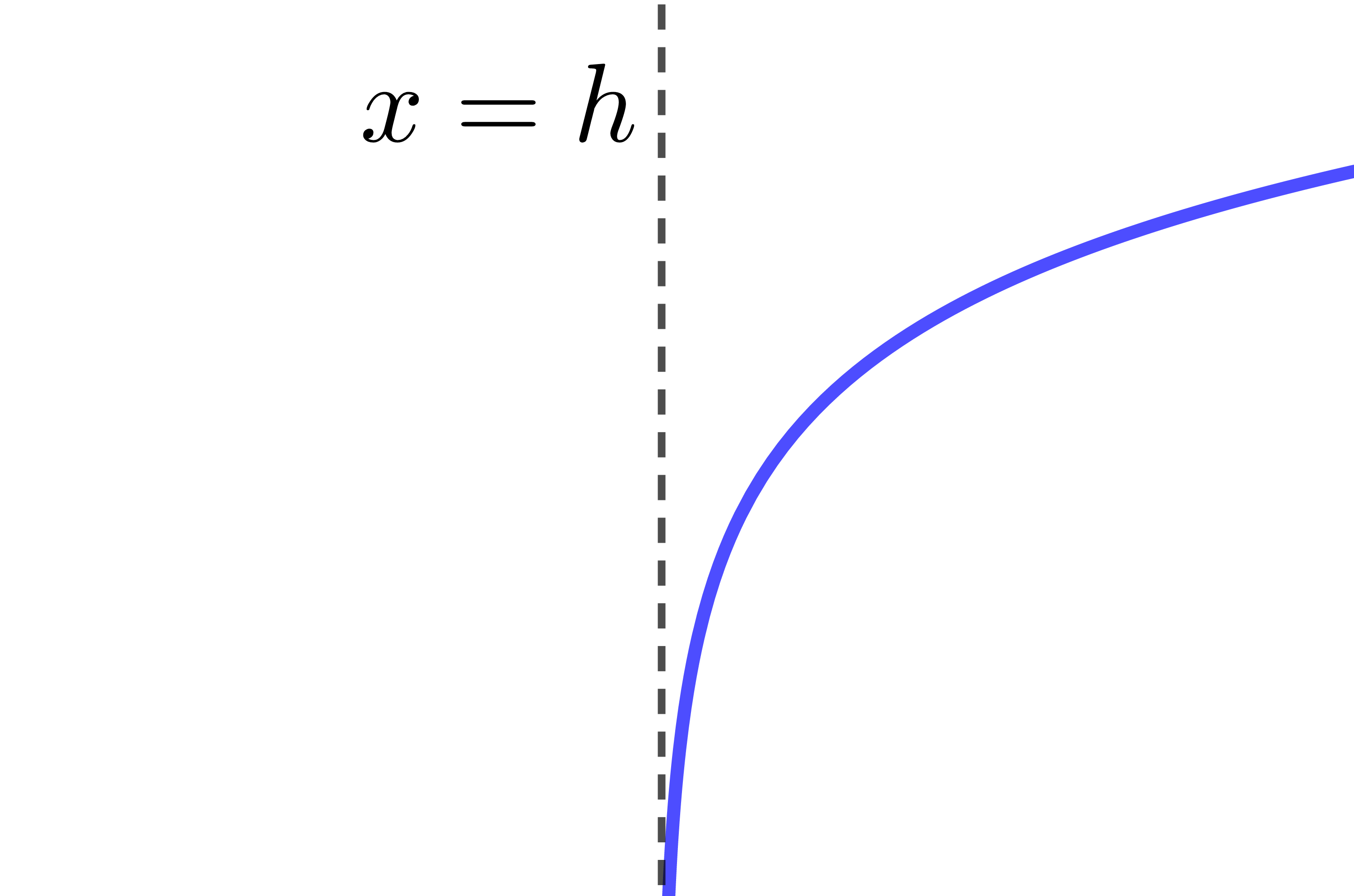 |
| |b<0| | 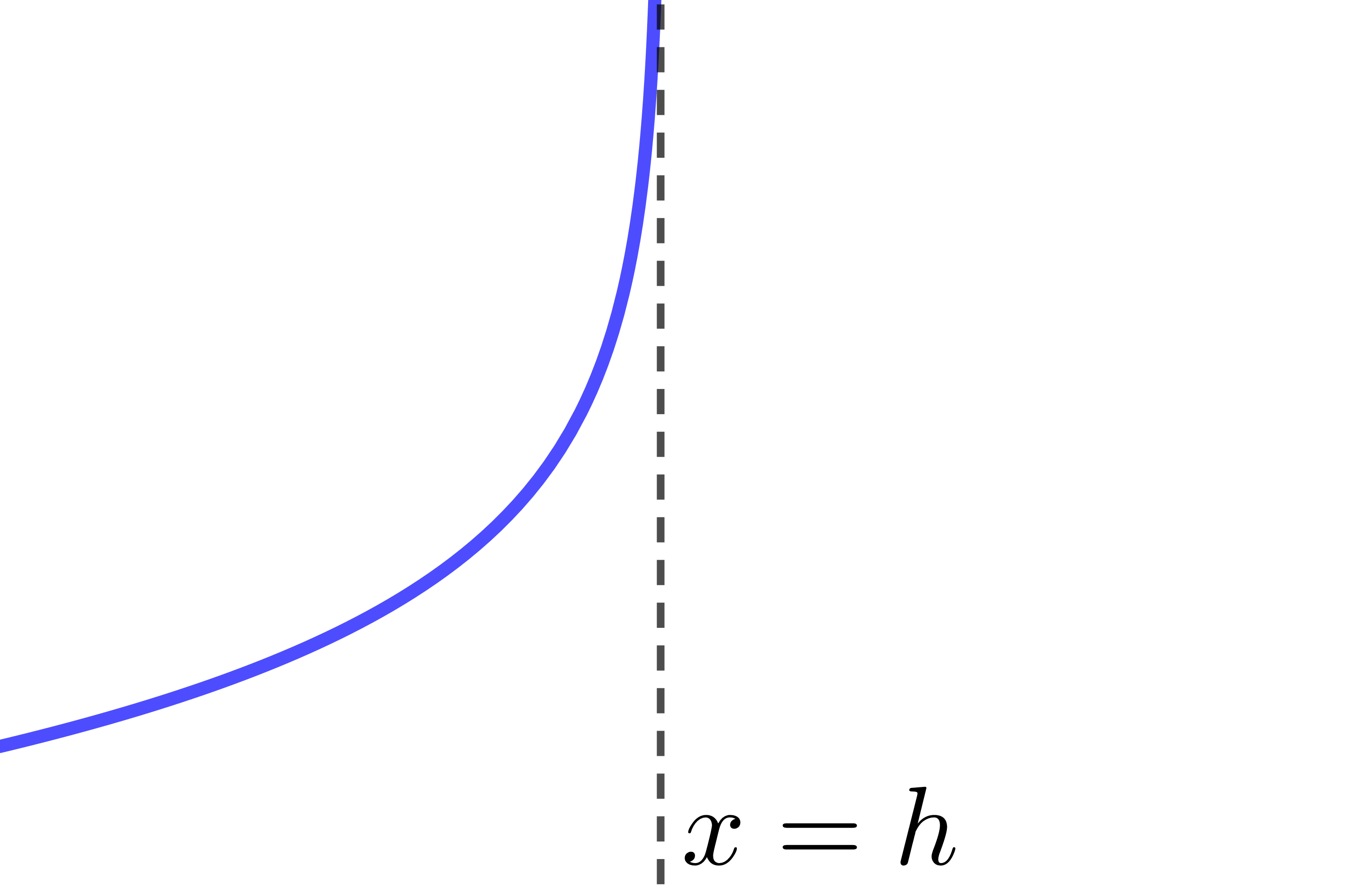 |
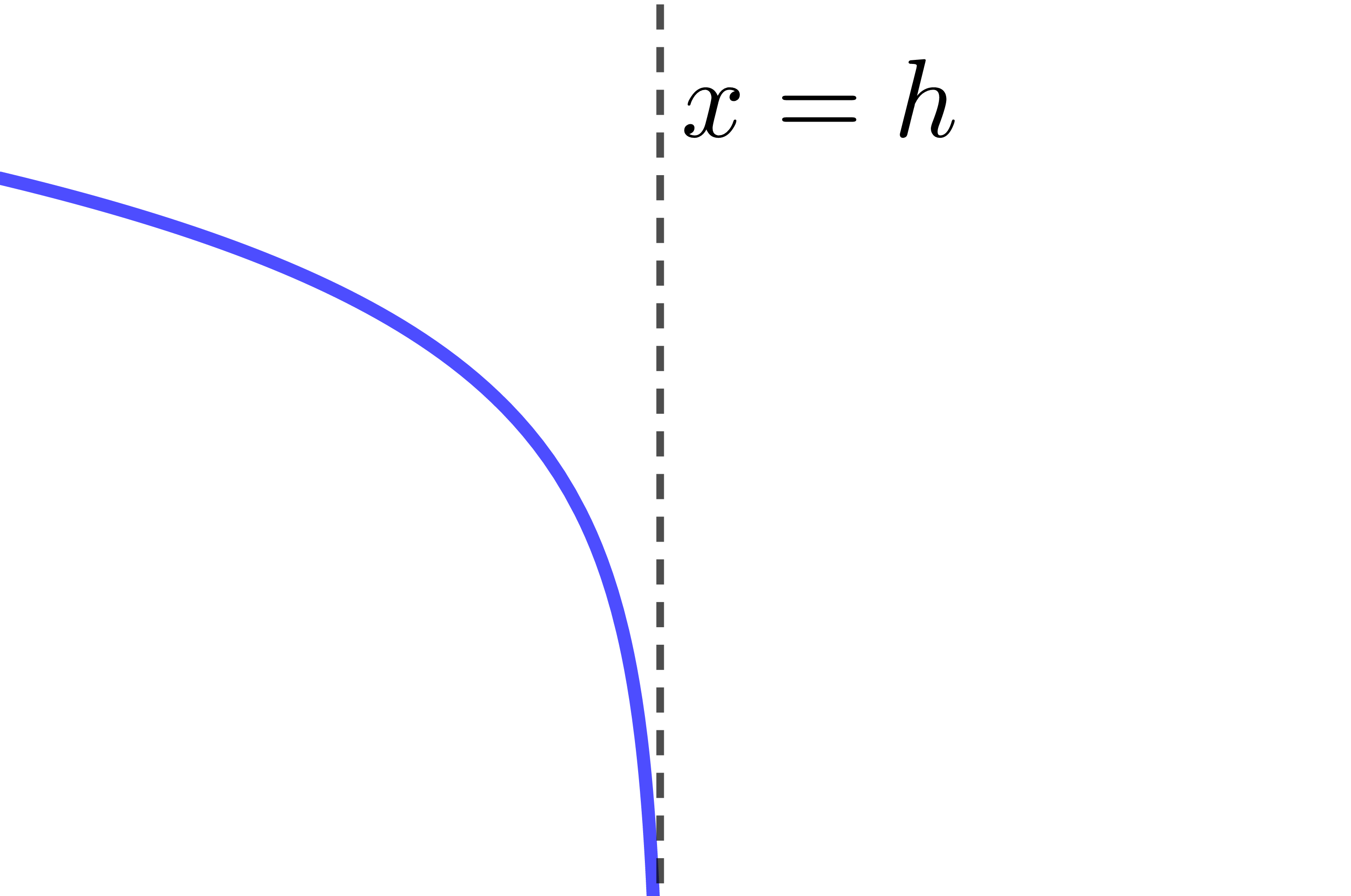 |
Comme on peut le voir en observant le tableau résumé ci-haut, certaines combinaisons de paramètres donnent le même résultat. Par exemple, |c>1,| |a>0| et |b>0| est équivalent à |0<c<1,| |a<0| et |b>0.| C'est pour cette raison qu'on simplifie souvent l'équation d'une fonction logarithmique en forme canonique en éliminant les paramètres |a| et |k.| ||\begin{align} f(x) &= a\log_c b(x-h)+k \\ \Rightarrow \ f(x) &= \log_c b(x-h) \end{align}||Pour cette façon simplifiée d'écrire la règle d'une fonction logarithmique, le tableau résumé sera :
| |b>0| | |b<0| | |
|---|---|---|
| |c>1| | 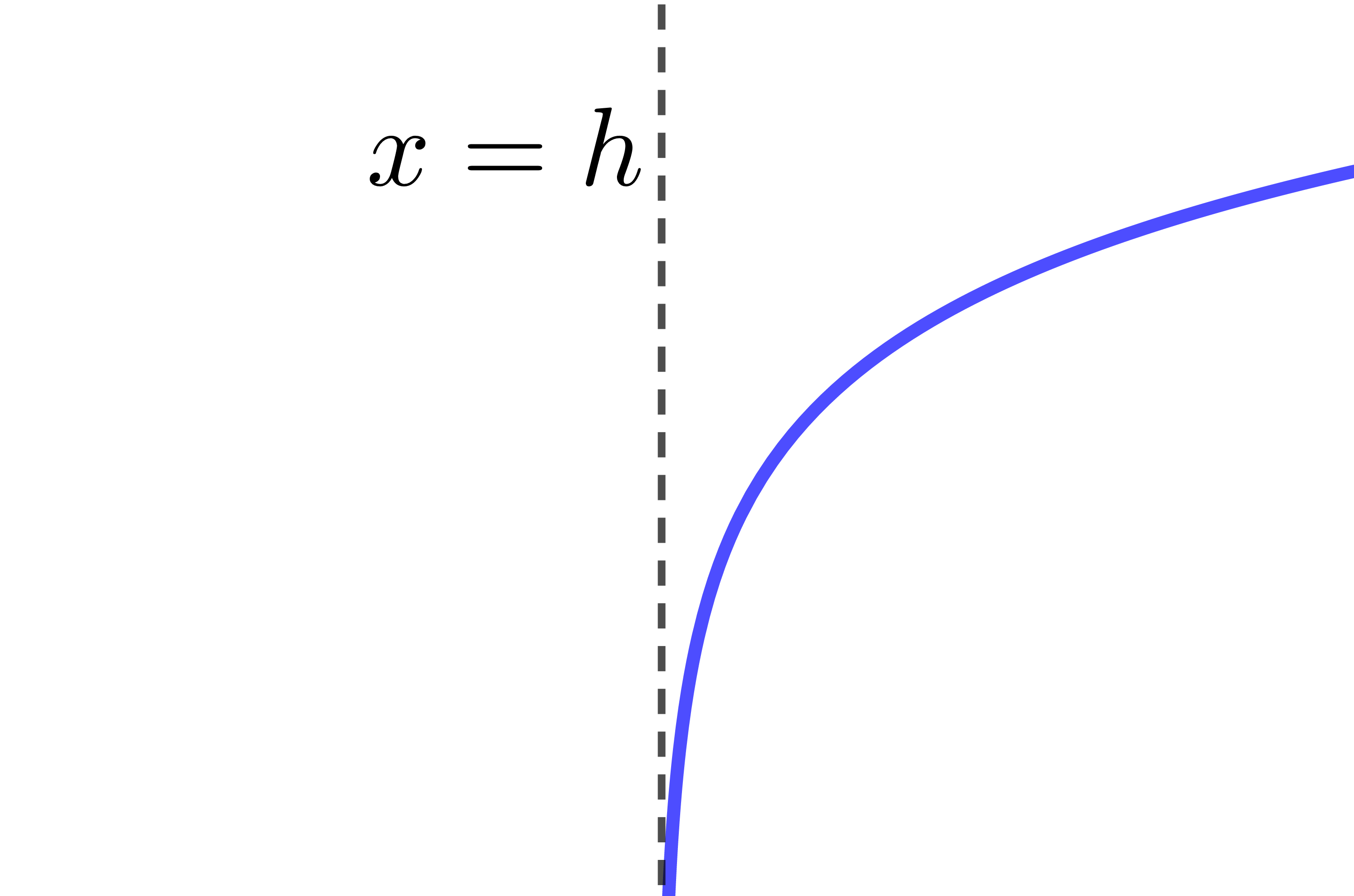 |
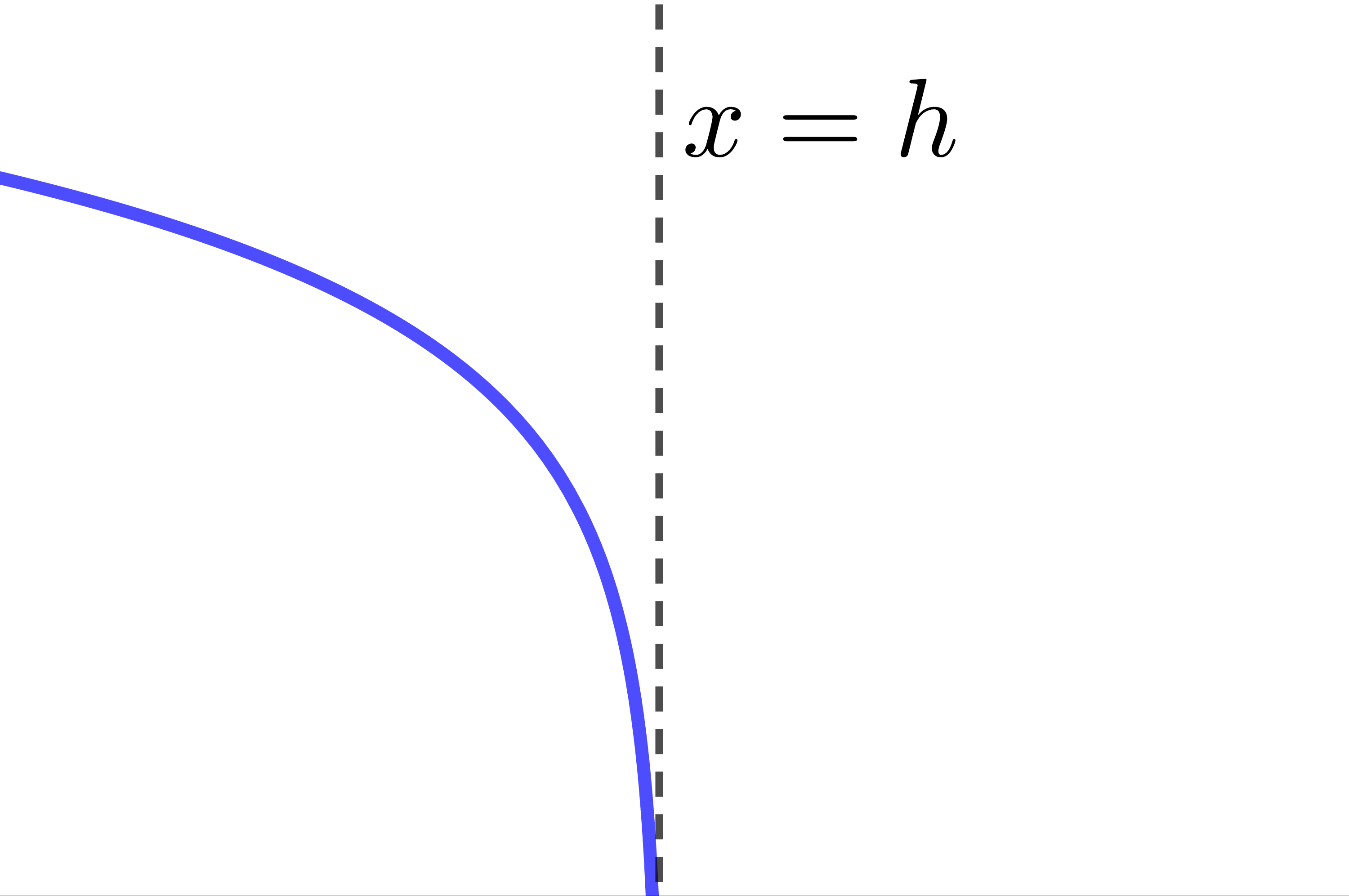 |
| |0<c<1| | 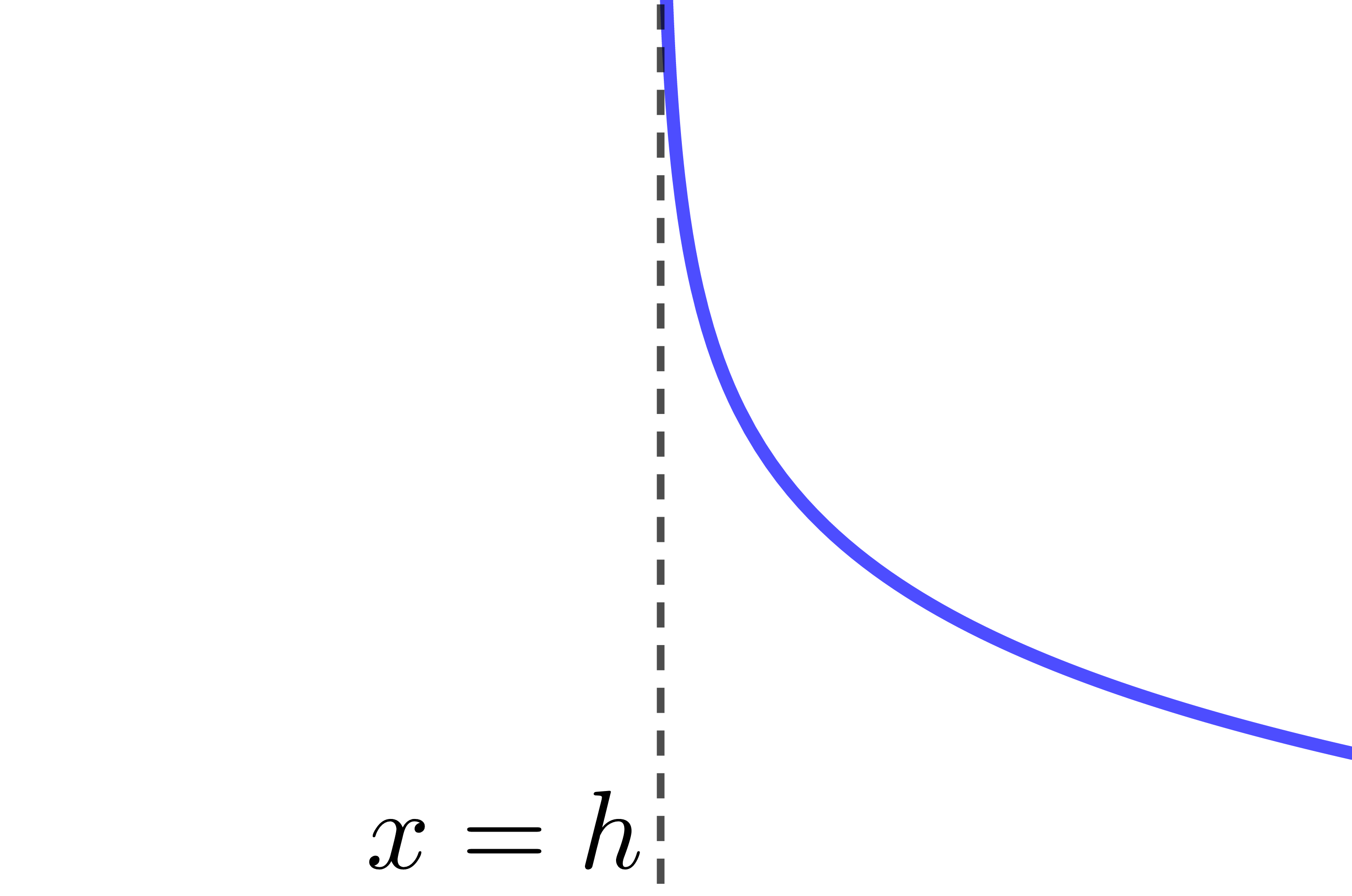 |
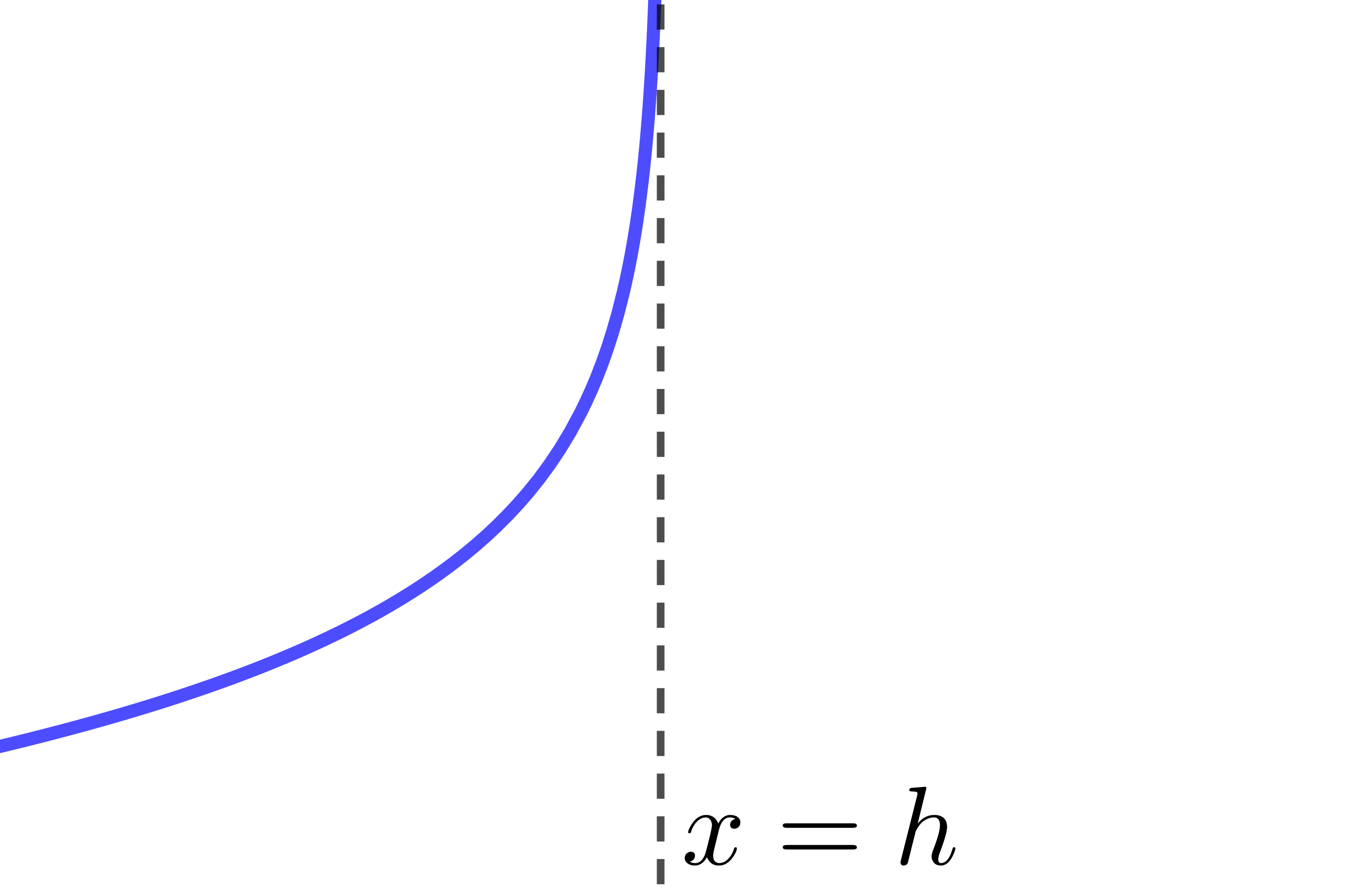 |
Dans cette page
- Haut de page
- Manipulation animée des paramètres
- L'analyse du paramètre |a| a
- Un changement d'échelle vertical à la fonction de facteur |a| a
- Une réflexion de la courbe de la fonction autour de l'axe des |x| x
- L'analyse du paramètre |b| b
- Un changement d'échelle horizontal de la fonction de facteur |\dfrac{1}{b}| 1b
- Une réflexion de la courbe de la fonction autour de l'axe des |y| y
- L'analyse de la base |c| c
- La variation de la fonction
- L'analyse du paramètre |h| h
- Une translation horizontale de toute la fonction
- L'analyse du paramètre |k| k
- Une translation verticale de toute la fonction
- Résumé
- À voir aussi